一种非均匀流场积分吸光度的计算方法和系统与流程

[0001]
本申请涉及一种非均匀流场积分吸光度的计算方法和系统，属于燃烧场二维重建技术领域。


背景技术：

[0002]
基于激光吸收光谱技术的燃烧场测量方法，相比于传统的侵入式测量方法具有灵敏度高、响应速度快、不干扰流场的优势。将激光吸收光谱方法与ct技术相结合，成为激光吸收光谱层析技术(tas)，可以实现对燃烧流场参数的二维分布测量。
[0003]
ct重建的思路是将被测区离散成网格，每个网格内参数均匀分布，一条光线的测量结果是其穿过网格参数沿光线穿过长度的积分量，即ct技术的引入条件是要找到“可积性”参数。在吸收光谱测量中，满足“可积性”的参数是积分吸光度，它是吸光度在频域中的积分结果，也称作吸收面积。直接吸收方法可以通过直接扫描吸收光强信号在频率上的积分获得积分吸光度，数学模型简单，可以直接获得“可积性”参数。但直接吸收在极端环境下，如振动、窗口污染、光线抖动等使得信号强度不稳定，给基线拟合带来较大偏差，这种偏差将被以真值的形式带入到二维重建中，尽管有很多研究者对二维重建算法进行改进以提高重建质量，但是这种偏差在后续的重建中很难被消除。波长调制光谱方法利用对激光波长的高频正弦调制可以有效地隔离低频噪声，使吸收光谱技术的工程应用能力得到了显著提高。但是现有技术中并没有如何在波长调制光谱中提取“可积性”参数的方法。


技术实现要素：

[0004]
本申请的目的在于，提供一种非均匀流场积分吸光度的计算方法和系统，以实现在波长调制光谱中提取“可积性”参数，将波长条调制光谱技术应用到燃烧场参数的二维重建测量中，为燃烧流场二维重建提供有效数据支持。
[0005]
本发明的第一实施例提供了一种非均匀流场积分吸光度的计算方法，包括：
[0006]
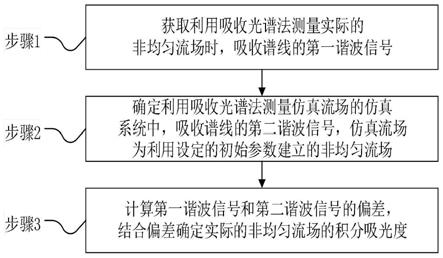
步骤1、获取利用吸收光谱法测量实际的非均匀流场时，吸收谱线的第一谐波信号；
[0007]
步骤2、确定利用吸收光谱法测量仿真流场的仿真系统中，吸收谱线的第二谐波信号，所述仿真流场为利用设定的初始参数建立的非均匀流场；
[0008]
步骤3、计算所述第一谐波信号和所述第二谐波信号的偏差，结合所述偏差确定所述实际的非均匀流场的积分吸光度。
[0009]
优选地，所述步骤3，具体为：
[0010]
计算所述第一谐波信号和所述第二谐波信号的偏差，如所述偏差小于设定阈值，则利用所述第二谐波信号对应的所述仿真流场的参数确定所述非均匀流场的积分吸光度；如所述偏差大于或等于所述设定阈值，则调整所述仿真流场的参数后，重复步骤3，直至所述偏差小于设定阈值。
[0011]
优选地，所述步骤2具体为：
[0012]
步骤2.1、确定所述仿真系统中，所述仿真流场在时域下的透射系数；所述透射系数为仅与所述吸收谱线的频率相关的2阶伏赫特线型函数；
[0013]
步骤2.2、结合所述透射系数和所述仿真系统中时域下的入射光强，计算所述仿真流场的透射光强；
[0014]
步骤2.3、解调所述透射光强，确定吸收谱线的所述第二谐波信号。
[0015]
优选地，所述步骤2.1具体为：
[0016]
利用第一公式确定所述仿真流场在时域下的透射系数，所述第一公式为：
[0017][0018]
式中，s为吸收谱线强度，t为仿真流场的温度，l为仿真流场的位置，χ为仿真流场的组分浓度，p为仿真流场的压强，为吸收谱线的n阶伏赫特线型函数，其中，φ
vi
(ν)(i为阶数且i＝1和2)为仅与所述吸收谱线的频率v相关的伏赫特线型函数，k
i
是权重系数，总和为1，且k
i
≥0。
[0019]
优选地，所述步骤2.2具体为：
[0020]
利用第二公式计算所述仿真流场的透射光强，所述第二公式为：
[0021]
i
t
＝i
0
·
τ
[0022]
式中，i
t
为透射光强，i
0
为入射光强，τ为透射系数。
[0023]
优选地，所述步骤2.3具体为：
[0024]
步骤2.3.1、利用数字锁相放大器，解调所述透射光强，得到一次谐波s
1f
和二次谐波的x分量x
2f
和y分量y
2f
；
[0025]
步骤2.3.2、利用第三公式计算所述吸收谱线的所述第二谐波信号，所述第三公式为：
[0026][0027]
式中，s
2f/1f
为第二谐波信号，x
2f
为二次谐波的x分量，
bg
x
2f
为背景信号的二次谐波的x分量，y
2f
为二次谐波的y分量，
bg
y
2f
为背景信号的二次谐波的y分量，s
1f
为一次谐波，
bg
s
1f
为背景信号的一次谐波。
[0028]
优选地，所述步骤3中计算所述第一谐波信号和所述第二谐波信号的偏差具体为：
[0029]
利用第四公式计算所述第一谐波信号和所述第二谐波信号的偏差，所述第四公式为：
[0030][0031]
式中，d为偏差，
mea
s
2f/1f
为所述第一谐波信号，
cal
s
2f/1f
为所述第二谐波信号。
[0032]
优选地，所述利用所述第二谐波信号对应的所述仿真流场的参数确定所述非均匀流场的积分吸光度，具体为：
[0033]
根据第五公式计算所述非均匀流场的积分吸光度，所述第五公式为：
[0034][0035]
式中，a为积分吸光度，s为吸收谱线强度，t为仿真流场的温度，l为仿真流场的位置，χ为仿真流场的组分浓度，p为仿真流场的压强。
[0036]
优选地，所述步骤3采用的算法为模拟退火算法；
[0037]
所述模拟退火算法中的目标函数为所述第四公式，约束条件为所述偏差小于设定阈值，优化变量为积分吸光度、洛伦兹线宽和高斯线宽；
[0038]
所述洛伦兹线宽和所述高斯线宽与所述伏赫特线型函数的关系满足第六公式，所述第六公式为：
[0039]
φ
v
＝f(δν
d
,δν
c
)
[0040]
式中，φ
v
为伏赫特线型函数，δν
c
为洛伦兹线宽，δν
d
高斯线宽。
[0041]
本发明的第二实施例提供了一种非均匀流场积分吸光度的计算系统，包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述方法的步骤。
[0042]
本发明的非均匀流场积分吸光度的计算方法相较于现有技术，具有如下有益效果：
[0043]
本发明的非均匀流场积分吸光度的计算方法，在波长调制光谱中提取“可积性”参数，将波长条调制光谱技术应用到燃烧场参数的二维重建测量中，为燃烧流场二维重建提供有效数据支持。
附图说明
[0044]
图1为本发明实施例中非均匀流场积分吸光度的计算方法的流程图；
[0045]
图2为用透射系数参数替换光谱参数和流场参数做s
2f/1f
仿真系统时的输入量；
[0046]
图3为本发明实施例中非均匀流场积分吸光度的计算方法的原理示意图；
[0047]
图4为100次实验中积分吸光度的解算结果；
[0048]
图5为图4对应的积分吸光度计算误差。
具体实施方式
[0049]
图1为本发明实施例中非均匀流场积分吸光度的计算方法的流程图。
[0050]
图3为本发明实施例中非均匀流场积分吸光度的计算方法的原理示意图。
[0051]
本发明的非均匀流场积分吸光度的计算方法，包括如下步骤：
[0052]
步骤1、获取利用吸收光谱法测量实际的非均匀流场时，吸收谱线的第一谐波信号；
[0053]
步骤2、确定利用吸收光谱法测量仿真流场的仿真系统中，吸收谱线的第二谐波信号，所述仿真流场为利用设定的初始参数建立的非均匀流场，该步骤的详细流程见图2，该步骤具体为:
[0054]
步骤2.1、确定仿真系统中，仿真流场在时域下的透射系数；透射系数为仅与吸收谱线的频率相关的2阶伏赫特线型函数；具体为：
[0055]
利用第一公式确定仿真流场在时域下的透射系数，第一公式为：
[0056][0057]
式中，s为吸收谱线强度，t为仿真流场的温度，l为仿真流场的位置，χ为仿真流场的组分浓度，p为仿真流场的压强，为吸收谱线的n阶伏赫特线型函数，其中，φ
vi
(ν)(i为阶数且i＝1和2)为仅与吸收谱线的频率v相关的伏赫特线型函数，k
i
是权重系数，总和为1，且k
i
≥0。
[0058]
步骤2.2、结合透射系数和仿真系统中时域下的入射光强，计算仿真流场的透射光强，具体为：
[0059]
利用第二公式计算仿真流场的透射光强，第二公式为：
[0060]
i
t
＝i
0
·
τ
[0061]
式中，i
t
为透射光强，i
0
为入射光强，τ为透射系数。
[0062]
步骤2.3、解调透射光强，获得吸收谱线的第二谐波信号，具体为：
[0063]
步骤2.3.1、利用数字锁相放大器，解调透射光强，得到一次谐波s
1f
和二次谐波的x分量x
2f
和y分量y
2f
；
[0064]
步骤2.3.2、利用第三公式计算吸收谱线的第二谐波信号，第三公式为：
[0065][0066]
式中，s
2f/1f
为第二谐波信号，x
2f
为二次谐波的x分量，
bg
x
2f
为背景信号的二次谐波的x分量，y
2f
为二次谐波的y分量，
bg
y
2f
为背景信号的二次谐波的y分量，s
1f
为一次谐波，
bg
s
1f
为背景信号的一次谐波。
[0067]
步骤3、获取仿真系统中，吸收谱线的第二谐波信号，具体为：
[0068]
计算所述第一谐波信号和所述第二谐波信号的偏差，如所述偏差小于设定阈值，则利用所述第二谐波信号对应的所述仿真流场的参数确定所述非均匀流场的积分吸光度；如所述偏差大于或等于所述设定阈值，则调整所述仿真流场的参数后，重复步骤3，直至所述偏差小于设定阈值。
[0069]
其中计算所述第一谐波信号和所述第二谐波信号的偏差，具体为：利用第四公式计算第一谐波信号和第二谐波信号的偏差，第四公式为：
[0070][0071]
式中，d为偏差，
mea
s
2f/1f
为第一谐波信号，
cal
s
2f/1f
为第二谐波信号。
[0072]
其中，利用第二谐波信号对应的仿真流场的参数确定非均匀流场的积分吸光度，具体为：根据第五公式计算非均匀流场的积分吸光度，第五公式为：
[0073][0074]
式中，a为积分吸光度，s为吸收谱线强度，t为仿真流场的温度，l为仿真流场的位置，χ为仿真流场的组分浓度，p为仿真流场的压强。
[0075]
上述步骤3优选使用模拟退火算法；
[0076]
模拟退火算法中的目标函数为第四公式，约束条件为偏差小于设定阈值，优化变量为积分吸光度、洛伦兹线宽和高斯线宽；
[0077]
洛伦兹线宽和高斯线宽与伏赫特线型函数的关系满足第六公式，第六公式为：
[0078]
φ
v
＝f(δν
d
,δν
c
)
[0079]
式中，φ
v
为伏赫特线型函数，δν
c
为洛伦兹线宽，δν
d
高斯线宽。
[0080]
本发明使用n阶伏赫特线型表示吸收谱线的原因为：
[0081]
(1)在非均匀流场下，线型函数φ(v,l)是随流场位置变化的量，创建针对φ(v,l)的解耦模型，消除φ与l的关联性，建立n阶伏赫特线型。
[0082]
在均匀流场下，透射光强可以表示为入射光强i
t
与透射系数τ的函数，即：
[0083]
i
t
＝i
0
·
τ＝i
0
·
exp(-a
·
φ
v
)
[0084]
在均匀流场下上式成立，但是对于非均匀流场下，φ(v,l)是随流场位置变化的量，因此不能直接将其从积分项中分离。为了分离积分吸光度a，需要创建一个针对φ的解耦模型，消除φ与l的关联性，利用多个与l无关的伏赫特线型函数的线性组合φ
(n)
来表示φ。
[0085]
定义n阶伏赫特线型φ
(n)
如下：
[0086]
φ
(n)
＝k
1
·
φ
v1
(ν)+k
2
·
φ
v2
(ν)+
…
+k
n
·
φ
vn
(ν)
[0087][0088]
k
i
≥0,i＝1,2,...,n
[0089]
其中，n为线性组合的阶数，φ
vi i＝1,2,
…
,n是伏赫特线型函数，仅是与吸收谱线的频率v相关的函数，k
i
是权重系数，总和为1，且k
i
≥0，k
i
的设置确保了伏赫特线型函数满足在频域上的积分为1的性质。
[0090]
由于φ
(n)
的组合分量都与l无关，可以分离出积分吸光度，即
[0091][0092]
其中s为吸收谱线强度，是与温度和吸收谱线相关的量，χ为组分浓度，p为压强。均匀流场时，线型函数为标准的伏赫特线型；而非均匀流场时，线型函数并非标准的伏赫特线型，可用多个标准的伏赫特线型函数的线性组合来表示。均匀流场的透射系数模型实际上是非均匀流场模型φ
(n)
的阶数n取1时的一个特例。
[0093]
进一步地，将伏赫特线型写成高斯线宽、洛伦兹线宽和权重系数的函数。
[0094]
伏赫特线型φ
v
是δν
c
和δν
d
的函数，即：
[0095]
φ
v
＝f(δν
d
,δν
c
)
[0096]
对于n阶伏赫特线型φ
(n)
，是n组δν
d(n)
和δν
c(n)
以及权重系数k
(n)
的函数，即：
[0097]
φ
(n)
＝f(k
(1)
,δν
d(1)
,δν
c(1)
,k
(2)
,δν
d(2)
,δν
c(2)
...k
(n)
,δν
d(n)
,δν
c(n)
)
[0098]
透射系数τ可用积分吸光度a和n组δν
d(n)
和δν
c(n)
以及权重系数k
(n)
的函数表示，即：
[0099]
τ＝f(a,k
(1)
,δν
d(1)
,δν
c(1)
,k
(2)
,δν
d(2)
,δν
c(2)
...k
(n)
,δν
d(n)
,δν
c(n)
)
[0100]
本申请以2阶伏赫特线型开展研究，并将两个线型的权重系数设为相等来进一步简化。此时透射系数τ可表示为
[0101]
τ＝f(a,δν
d(1)
,δν
c(1)
,δν
d(2)
,δν
c(2)
)
[0102]
即透射系数τ由a、δν
d(1)
、δν
c(1)
、δν
d(2)
和δν
c(2)
等五个参数决定。
[0103]
在上述使用n阶伏赫特线型表示吸收谱线的基础上，建立利用吸收光谱法测量仿真流场的仿真系统，仿真流场为利用设定的初始参数建立的非均匀流场，模拟透射光信号，再利用数字锁相放大器解调，从而获取二次谐波信号s
2f/1f
。
[0104]
(1)将积分吸光度a和两组洛伦兹线宽和高斯线宽作为参数，设计流场模型(该流场模型中的参数为初始设定的参数，包括温度t、组分浓度χ和压强p)，根据光谱参数(吸收谱线中心频率v
0
、下态能级e
″
、吸收谱线强度s(t
0
)、自展宽系数γ
self
(t
0
)、空气展宽系数γ
air
(t
0
)、自展宽指数n
self
和空气展宽指数n
air
)，和激光频率信号v(t)，计算时域下的透射系数τ(t)；
[0105]
(2)根据beer-lambert定律，由时域下的入射光强i
0
(t)和透射系数τ(t)，计算透射光强i
t
(t)；
[0106]
(3)利用数字锁相放大器，解调透射光信号i
t
(t)，得出各次谐波信号的x分量和y分量，计算s
2f/1f
；
[0107]
(4)减去背景信号的谐波信号，其中背景信号等同于无吸收时的谐波信号，设背景信号的n次谐波信号为
bg
s
nf
其对应的x、y分量分别为
bg
x
nf
和
bg
y
nf
，减去背景信号后的2f/1f信号可由下式表示
[0108][0109]
最后以积分吸光度a、洛伦兹线宽δν
c
和高斯线宽δν
d
作为优化变量，创建目标函数，采用模拟退火算法求解积分吸光度。
[0110]
(1)计算实验测量的二次谐波信号，标记为
mea
s
2f/1f
；
[0111]
(2)利用上述步骤仿真系统得到的二次谐波信号，标记为
cal
s
2f/1f
；
[0112]
(3)计算
mea
s
2f/1f
与
cal
s
2f/1f
的偏差，计算公式为
[0113][0114]
当实际的透射系数与猜想的透射系数相同时，
mea
s
2f/1f
将与
cal
s
2f/1f
相同，反之则存在偏差；
[0115]
(4)利用模拟退火算法，对步骤(3)中的计算偏差公式作为目标函数，求解积分吸光度。
[0116]
本发明还公开了一种非均匀流场积分吸光度的计算系统，包括存储器、处理器以及存储在存储器中并可在处理器上运行的计算机程序，处理器执行计算机程序时实现上述方法的步骤。
[0117]
下面将以具体的实施例说明本发明的方法。
[0118]
实例：三个流场参数t、χ、p均为高斯分布，参数取值范围是：温度t为300～2800k、组分浓度χ为0.05～0.5、压强p为0.7～1.6atm，光程设为20cm，用7185.6cm-1
模拟测量的积分吸光度为8.108
×
10-2
。
[0119]
分别采用1阶模型和2阶模型重复100次，计算积分吸光度，积分吸光度结果如图4所示，测量偏差如图5所示。
[0120]
一阶模型的结果存在约1.4％的偏差，二阶模型的结果的平均误差约为0.3％，表明二阶伏赫特线型更接近真实线型分布。二阶模型的计算结果浮动较大，这是因为二阶模型的参数更多，导致不确定性增加。
[0121]
本发明可以实现对非均匀流场积分吸光度的求解，可以用于燃烧场参数二维重建测量。
[0122]
以上所述，仅是本申请的几个实施例，并非对本申请做任何形式的限制，虽然本申请以较佳实施例揭示如上，然而并非用以限制本申请，任何熟悉本专业的技术人员，在不脱离本申请技术方案的范围内，利用上述揭示的技术内容做出些许的变动或修饰均等同于等效实施案例，均属于技术方案范围内。