一种动力电池全生命周期内SOC和容量在线联合估计方法与流程

一种动力电池全生命周期内soc和容量在线联合估计方法
技术领域
1.本发明设计电动汽车动力电池管理技术领域，尤其涉及一种考虑电池容量动态特性和不同老化程度的动力电池全生命周期内soc和容量在线联合估计方法。
技术背景
2.电池管理系统是电动汽车的核心部件之一，通过对电池系统的状态更新、故障检测以及均衡控制，可以保证动力电池安全可靠的运行。其中，最重要的功能就是实现动力电池全生命周期内soc和容量的估计与更新。然而，动力电池的强非线性特性以及温度、倍率、老化状态等因素的影响，都导致电池状态的准确估计变得十分困难。
3.目前常用的电池soc估计方法是基于等效电路模型和滤波器实现的，然而等效电路模型只能反映电池的电压动态特性，忽略了电池容量的动态变化，不能很好的反映电池完整的动态非线性特性。此外，卡尔曼滤波是目前最常用的电池状态估计方法，虽然可以有效提高soc的估计精度和鲁棒性，但其计算量较大，对硬件要求较高。
4.动力电池soc和当前老化状态下的最大可用容量是直接相关的，对soc和容量进行联合估计是十分必要的。目前大多采用两个不同时间尺度的滤波器同时估计电池soc和容量，但本质上还是基于soc 的电池容量估计。该方法忽略了soc本身的估计误差，算法中存在误差的传递。
5.本发明首先在thevenin模型的基础上考虑了电池容量的动态特性，提出了一种混合电池模型，并对soc计算式进行了修正。其次，提出了一种惯性系数指数衰减的粒子群算法用于在线辨识包括电池开路电压在内的模型参数，能有效平衡参数辨识速度和精度。最后，设计了一种非线性pi观测器用来估算电池soc，其计算量明显小于目前常用的卡尔曼滤波和粒子滤波算法，并利用特定时间内的累计电荷量、电池开路电压和不可用容量的变化在线辨识电池当前老化状态下的最大可用容量。


技术实现要素：

6.为解决上述本领域中存在的技术问题，本发明开发了一种动力电池全生命周期内soc和容量在线联合估计方法，能有效提高电池状态估计精度、降低计算量。
7.本发明的具体技术方案包括如下步骤：
8.步骤一、在所述动力电池充放电测试中，以1秒为采样间隔对电池的端电压、充放电电流进行采样；
9.步骤二、基于所述实验获得的不同条件下的电池容量测试数据实现电池容量动态特性建模，并对现有soc定义进行修正；
10.步骤三、基于实验数据建立电池等效电路模型，将开路电压作为待辨识参数，并结合基尔霍夫定理得到电池等效模型的离散数学表达式；
11.步骤四、设计一种惯性系数指数衰减的粒子群算法在线辨识模型参数；
12.步骤五、重构考虑了容量动态特性的动力电池状态空间方程，设计一种基于模型
的非线性pi观测器估计电池soc，并对不同老化状态下的电池容量进行估计和更新。
13.所述步骤二中将电池容量分为可用容量和储存容量，储存容量需转换成可用容量才能输出，无法转换的容量则为不可用容量，对应不可用容量的离散方程为：
[0014][0015]
其中，c
not
表示电池当前工作状态下的不可用容量，δ(t0)表示电池可用容量部分和储存容量部分之间的初始高度差，i表示电池的工作电流，c表示某一工况下电池放出的实际电量与当前老化状态下的电池最大可用容量的比值，k
′
反映储存容量转换成可用容量的能力。
[0016]
根据不同老化状态、放电倍率下电池可以放出的实际容量采用离线统计分析手段，再结合优化算法，可以获得对应条件下电池不可用容量方程中的c和k
′
等特性参数。
[0017]
在soc定义中引入电池不可用容量，对应修正后的soc为：
[0018][0019]
其中，soc
ea
(t)表示t时刻的电池soc，c
available
(t)表示t时刻电池在当前放电条件下的剩余可用电量，c
max
表示电池当前老化状态下的最大可用容量，c
not
(t)表示t时刻电池在当前放点条件下的不可用容量，i(t)为t时刻的工作电流。
[0020]
步骤三所述的电池等效电路模型采用thevenin模型，根据基尔霍夫定理得到用于参数辨识的端电压离散数学表达式：
[0021][0022]
其中，r0表示电池的欧姆内阻，r1表示电池的极化电阻，c1表示电池的极化电容，v0表示电池的端电压，e0表示电池的开路电压，θ(r0,r1,c1,e0)＝[θ1θ2θ3θ4]为待辨识参数矩阵，μ(i,v0)＝[μ1μ2μ3μ4] 为系统输入矩阵；
[0023]
进一步地，电池模型参数可以表示为：
[0024][0025]
步骤四所述的模型参数在线辨识采用改进粒子群算法实现，具体如下：
[0026]
随机生成n个维度为m的粒子并为每个粒子初始化速度和惯性系数ω0，其中 n代表粒子群中的粒子总数，m代表需要辨识的参数个数；
[0027]
随机指定粒子群中的一个粒子作为当前初始全局最优粒子，该粒子各维度对应的值分别对应 thevenin模型中的各个参数；
[0028]
使用当前的电池模型参数和采集的t时刻电池电流数据，利用电池模型离散数学表达式计算得到t 时刻电池端电压的估计值
[0029]
更新所有粒子的适应度值，将端电压估计误差最小的粒子选取为当前时刻的参数
最优粒子，评价函数如下：
[0030][0031]
式中，e表示粒子群算法目标函数的误差，表示t时刻序号i对应的粒子在进行k次迭代优化之后计算得到的电池端电压估计值。
[0032]
根据粒子的适应度更新其速度和位置，粒子的惯性系数按照指数衰减的方式变化，t+1时刻粒子位置和速度为：
[0033][0034]
ω
k
＝ω0·
e
‑
α
·
k/n
[0035]
式中，ζ和η为[0,1]之间的随机数。c1和c2为学习因子。p
i,j
为第i个粒子的个体最优位置，p
g
为全局最优粒子的位置，为第i个粒子在第k次迭代之后的位置，ω
k
为粒子在第k次迭代之后的惯性系数，ω0为粒子初始惯性系数，α为粒子惯性系数的衰减指数，n为粒子群算法每次参数辨识过程中设定的迭代次数。
[0036]
用n次迭代之后粒子群中的全局最优粒子的位置作为电池当前状态下的参数辨识结果；
[0037]
进一步地，由于电池参数是缓变参数，利用蒙特卡洛理论在当前时刻最优解附件重新生成随机粒子群并初始化粒子速度和惯性系数。
[0038]
重复执行步骤[0028]
‑
[0037]，用前一采样时刻得到的全局最优粒子作为下一时刻的初始全局最优粒子，实现电池参数的实时在线辨识。
[0039]
步骤五中构建了一种不同老化状态下电池soc和最大可用容量联合估计方法，具体如下：
[0040]
基于在线辨识的电池开路电压和实验测试结果重构开路电压表达式：
[0041][0042]
其中，e
0,offline
为离线拟合的开路电压，e
0,online
为在线辨识的开路电压，λ和β为开路电压离线和在线估计结果的比例系数，和为重构后的开路电压表达式系数。
[0043]
基于所述混合电池模型更新动力电池状态空间方程：
[0044][0045]
其中，
[0046][0047]
式中，x
t
表示电池系统t时刻的状态向量，u
t
表示t时刻的输入向量，y
t
表示t时刻电池模型的输出结果；采用非线性pi观测器结合不同老化状态下的电池最大可用容量，对所述电池系统的soc进行在线估计，得到t时刻的电池soc估计值soc
t
。
[0048]
进一步地，所述动力电池在不同老化状态下的最大可用容量通过以下方式计算：
[0049][0050]
通过soc的定义反推获得电池容量估计表达式，同时在容量估计过程中考虑了不可用容量部分。电池soc(t1)和soc(t2)分别为t1和t2采样时刻对应的电池soc，利用在线辨识的开路电压数据通过ocv
‑ꢀ
soc表查表获得。
[0051]
相对于现有技术，本发明具有如下的优点：
[0052]
本发明充分考虑了电池动态特性变化规律，在等效电路模型的基础上建立了考虑电池容量动态特性的混合电池模型，并在电池soc的定义中考虑了不可用容量部分；此外，考虑到电池参数受实际工作条件影响，改进了一种改进粒子群算法在线辨识模型参数，能有效平衡参数辨识速度和精度；同时，引入了非线性pi观测器估计电池soc，并对不同老化状态下的电池最大可用容量进行估计和更新。该方法能够准确估算电池不同老化状态下的soc和容量，且结构简单，有利于硬件实现。
附图说明：
[0053]
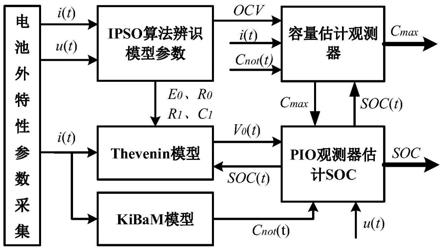
图1为本发明所提供方法的原理示意图；
[0054]
图2为本发明所述的电池性能测试实验电流数据；
[0055]
图3为本发明所述的电池容量动态特性模型；
[0056]
图4为本发明所述基于改进粒子群算法的参数辨识结果；
[0057]
图5为100次老化状态下电池循环工况的soc估算结果；
[0058]
图6为100次和400次老化状态下，本发明提供方法得到的容量估算结果。
具体实施方式
[0059]
下面结合附图对本发明做进一步的详细说明，以令本领域技术人员参照说明书能够得以实施。注意，附图所述实施例并不是本发明的全部实施例。
[0060]
如图1所示，本发明提供了一种电池全生命周期内soc和容量在线联合估算方法，依次按照以下所提供的步骤执行：
[0061]
步骤1：根据不同测试条件下恒流充放电测试和混合脉冲测试(hybrid pulse power characteristic, hppc)获得不同条件下的电池实际放电容量和开路电压数据；
[0062]
步骤2：根据步骤1得到的实验数据对电池不可用容量进行建模，结合thevenin模型构建混合电池模型，并对现有soc定义进行修正；
[0063]
步骤3：利用改进粒子群算法，结合thevenin模型和实时采集的电池电流、端电压参数，在线辨识包括开路电压在内的模型参数；
[0064]
步骤4：利用步骤2建立的混合电池模型建立非线性pi观测器估计电池soc，并实现soc和电池最大可用容量的联合估计。
[0065]
在本发明的一实施例中，以额定电压为3.6v，额定容量为2.6ah的三元材料18650锂离子电池为实验对象。首先采用恒流充放电测试，获得不同老化状态(100、200、300、400次循环)下、不同放电倍率(0.2c、0.5c、1c、1.5c、2c)下的实际放电容量，对电池容量动态特
性进行建模，将0.2c下测得的电池容量作为当前老化状态下的最大可用容量；此外，在不同老化状态下执行图2(a)所示的hppc测试工况，离线获得电池不同soc下的开路电压数据，并拟合ocv
‑
soc曲线；最后，验证工况则采用如图2(b)所示的udds联邦城市工况，实时测量记录电池工作过程中的电流、端电压数据，采样周期都为1秒。
[0066]
在获取电池最大可用容量和和不同放电倍率下的实际可用容量后，对本发明所述容量动态特性模型参数进行离线辨识。图3中y1和y2是总可用电荷和储存电荷，c是可用电荷和储存电荷的容量比，k为阀门宽度，需要辨识c和k这两个参数。
[0067]
电池当前老化状态下的最大可用容量为两种电荷初始值之和y0(即y
1,0
+y
2,0
),极限大电流倍率下 (本发明实施例中选择为4c)测试的实际放电电流为初始可用电荷y
1,0
，即可推出y
2,0
＝y0‑
y
1,0
。容量比可以表示为c＝y
1,0
/y0，然后根据测试数据、c值以及不可用容量公式，利用牛顿法求解k值的最优解。
[0068]
根据验证工况实时采集的电流、端电压数据，利用改进粒子群算法在线辨识thevenin模型参数。在粒子群位置进行更新过程中，每一次迭代都会有一个最优位置粒子，将这个最优粒子与上一时刻的全局最优解比较，如果当前最优解对应的电池模型端电压误差更小，则对全局最优粒子位置进行更新，具体如下。
[0069][0070]
此外，粒子在更新位置的过程中也可能会出现越过设定的上下边界的情况，算法将这部分越界的粒子退回到其个体历史最优解位置重新参与下一轮迭代，具体如下：
[0071][0072]
本发明实施例中提供的改进粒子群算法参数为：n＝n＝30，c1＝c2＝2，ω0＝0.8，α＝1.43。图4为模型参数在线辨识结果，可以看出，具有初始误差的估计参数可以快速收敛到真实值，然后以较小的误差波动。
[0073]
本实施例中采用非线性pi观测器估计电池soc，根据混合电池模型设计了观测器结构。注意，本发明根据在线和离线辨识的开路电压数据对其表达式进行了重构：
[0074][0075]
λ和β为开路电压离线和在线估计结果的比例系数，本实施例中采用的比例系数为0.7和0.3。
[0076]
图5是100次老化状态下，存在20％初始soc误差情况下，不同估算方法得到的soc结果对比图。3种不同soc估算策略分别是最小二乘算法和扩展卡尔曼滤波结合的方法(rls
‑
ekf)、双扩展卡尔曼滤波算法(dekf),以及本专利提出的改进粒子群算法和pi观测器结合的方法(ipso
‑
pio)。可以看出，即使初始soc不准确，本发明提出的ipso
‑
pio方法也能保证估计结果快速收敛到真实值，且在对比的三种算法中准确度最高，可以将估计误差控制在1％以内。
[0077]
图6是100次和400次老化状态下的电池最大可用容量在线估计结果。由于容量是基于累计电荷和开路电压变化估计的，容量估计在开始时会有一个收敛期，但能在12min内快速收敛并趋于稳定。因为本发明容量估计策略是在线估计、离线更新，所以在整个放电阶
段内记录容量估计结果，以容量估计结果平稳变化阶段(30％
‑
70％soc区间)的平均值作为当前老化状态下的容量最终估计结果，估计值与真实值之间的误差可以控制在2％以内。
[0078]
由此可见，由于考虑了电池容量的动态特性和不同老化程度的影响，本发明所述方法可以获得较为准确的电池soc和容量估计结果，此外算法结构简单、易于实现。
[0079]
当然，尽管已经介绍了本发明的实施例，但本发明也并不仅限于上述举例，本领域的技术人员在本发明范围内所做出的变化、修改和变型，也都应属于本发明的保护范围。