一种四臂螺旋天线数据拟合测角方法与流程

本发明涉及雷达技术领域，尤其是一种四臂螺旋天线数据拟合测角方法。

背景技术：

测角是雷达信号处理最为关键的应用，角度测量为后端的雷达信号进一步处理和利用提供了基础性信息，目前最常用的两种测角体制是单脉冲测角和相位干涉仪测角。相位干涉仪测角系统利用成对天线接收模板的连续波载波的信号相位差，得到目标偏离信号轴的量值和方向有关的误差信号，相位干涉仪测角体制虽然跟踪精度高，但是调试难度大，而且存在解模糊问题。因此目前更常用的是虽然测角精度略差于相位干涉仪测角，但结构简单、应用广泛的单脉冲测角体制。

单脉冲测角理论上只需要一个回波脉冲就可以确定目标角误差信息，在工程上，通常对多个回波脉冲进行积累，以提高检测概率和角误差测量精度。单脉冲测角系统利用成对波束接收目标信号的振幅或相位同时比较，得到目标偏离等信号轴的量值和方向有关的误差信号。因此，单脉冲测角又分为比相单脉冲测角和比幅单脉冲测角：比相单脉冲测角多应用于馈源较分散的阵天线系统，同时对信号的相位差进行比较得到角度误差值；而比幅单脉冲测角多用于馈源集中的面天线系统，同时对信号的幅度差进行比较得到角度误差值。

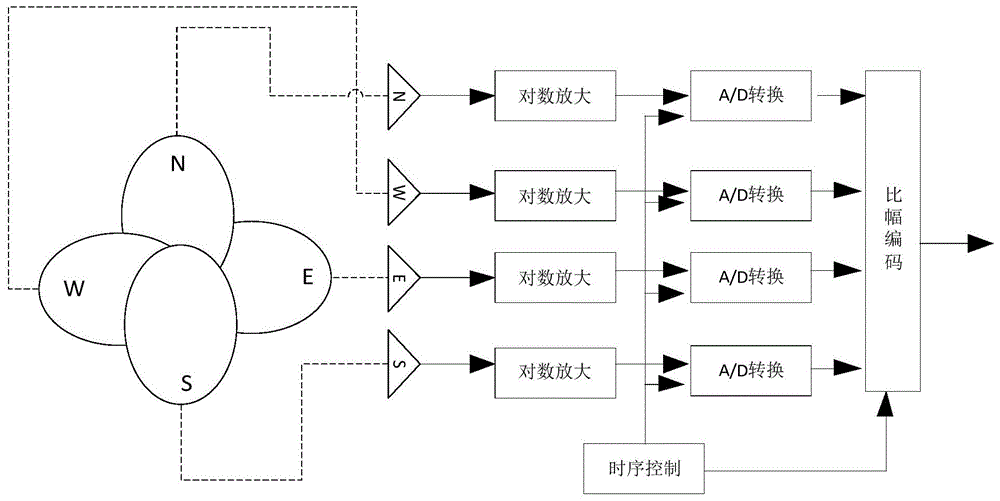
比幅单脉冲测角采用多个独立天线来产生多个独立的毗邻波束覆盖360度方位，这些天线采用相同的方向图函数f(θ)，且均匀分布，相邻天线的张角θs＝360°/m，各个天线的方位指向分别为fi(θ)＝f(θ-iθs)i＝0,1,…,m-1，k是天线的数量。通常使用的有四天线、六天线、八天线，这些天线的工作原理基本相似，测向精度随着天线数量的增加而提高。以包含四个天线的四天线全向振幅单脉冲测角系统为例，四天线方向图及对应的数字接收机系统框图请参考图1，每个天线的张角为90°，每个天线接收的信号经过各自振幅响应为ki的接收通道，输出脉冲的对数包络信号为si＝log[kif(θ-iθs)a(t)]i＝0,1,…,m-1，其中a(t)为雷达信号的振幅调制，该对数包络信号送给信号处理机后，由信号处理机产生对应的角度估值。具体的：在上述系统中，总有一对相邻波束分别输出最强和次强的信号，通过比较这对相邻波束输出信号包络幅度的相对大小，就可以确定雷达方位。如图2所示，假设天线方向图满足图2所示的振幅方向对称性，即f(θ)＝f(-θ)，那么雷达方向位于两个天线之间且偏离天线等信号方向的夹角为时，对应的通道输出信号分别为即相减之后，以分贝为单位的对数电压比r为若f(θ)函数在区间[-θs,θs]内具有单调性，也即满足f(θ1)<f(θ2)θ1,θ2∈[-θs,θs]，那么对数电压比r与之间也具有这种单调的对应关系，由r大小，从而便可得目标的角度信息。

平面螺旋天线可通过对称臂之间的波束关系确定角度信息，四臂螺旋可通过两个对称臂之间的关系来确定方位和俯仰以达到测角的目的，由于其具有宽波束、宽频带、圆极化等特性而被广泛地应用在gps和pcs等领域。在基于四臂螺旋天线的被动测向系统中，可以采用上述方法进行测角，但对于实际的测角系统而言，天线的方向图函数复杂化会导致具体的解算r与之间的函数无解析解，工程应用上通过实验获取各个方向的角度与雷达天线之间波束大小的关系，制作具体的查找表，在实际使用的过程中通过查找表来获取相应的角度。但查表法有两大缺点：1，表数据占用大量的内存单元；2，查表法比较会浪费查找时间，查找算法执行不好，查找时间会相应变慢，这也给实时处理系统带来一定的挑战。

技术实现要素：

本发明人针对上述问题及技术需求，提出了一种四臂螺旋天线数据拟合测角方法，本发明的技术方案如下：

一种四臂螺旋天线数据拟合测角方法，该方法包括：

利用基于四臂螺旋天线的被动测向系统对不同角度处的样本目标进行测向，在每一次测向中确定样本目标在天线坐标系中的目标来向以及对应的通过四臂螺旋天线获取到的四个原始天线波束得到一组样本数据；

基于样本数据拟合得到第一函数关系，第一函数关系是第一角度与四个原始天线波束之间的函数关系，第一角度是目标来向与天线坐标系的水平面之间的夹角；

基于样本数据拟合得到第二函数关系，第二函数关系是基于目标来向确定的俯仰角和方位角与四个原始天线波束之间的函数关系；

利用基于四臂螺旋天线的被动测向系统获取待测目标的四个原始天线波束；

利用待测目标的四个原始天线波束基于第一函数关系得到第一角度第一预估值；

利用待测目标的四个原始天线波束基于第二函数关系得到俯仰角预估值和方位角预估值，并基于俯仰角预估值和方位角预估值得到第一角度第二预估值和第二角度预估值，第二角度预估值是待测目标的目标来向在水平面上的投影与预定指向之间的夹角；

根据第一角度第一预估值、第一角度第二预估值和第二角度预估值修正俯仰角预估值和方位角预估值得到待测目标的俯仰角和方位角。

其进一步的技术方案为，根据第一角度第一预估值、第一角度第二预估值和第二角度预估值修正俯仰角预估值和方位角预估值得到待测目标的俯仰角和方位角，包括：

当第一角度第一预估值和第一角度第二预估值之间的差值达到预定阈值时，利用第一角度第一预估值和第二角度预估值修正俯仰角预估值和方位角预估值得到待测目标的俯仰角和方位角；

当第一角度第一预估值和第一角度第二预估值之间的差值未达到预定阈值时，将俯仰角预估值作为待测目标的俯仰角，将方位角预估值作为待测目标的方位角。

其进一步的技术方案为，利用第一角度第一预估值和第二角度预估值修正俯仰角预估值和方位角预估值得到待测目标的俯仰角和方位角，包括：

修正俯仰角预估值为β＝tan^-1(cosφ0tanθ1)得到待测目标的俯仰角，修正方位角预估值为α＝sin^-1(sinφ0sinθ1)得到待测目标的方位角，φ0为第二角度预估值，θ1为第一角度第一预估值。

其进一步的技术方案为，基于俯仰角预估值和方位角预估值得到第一角度第二预估值和第二角度预估值，包括：

确定第一角度第二预估值为θ2＝cos^-1(cos(β0)cos(α0))，确定第二角度预估值为φ0＝tan^-1(tan(β0)/sin(α0))，其中α0为方位角预估值，β0为俯仰角预估值。

其进一步的技术方案为，每组样本数据中的样本目标的目标来向指示样本目标的第一角度，则基于样本数据拟合得到第一函数关系，包括：

对于每个样本数据，计算样本数据的四个原始天线波束的和波束和差波束，并计算差波束与和波束的比值得到差模和模比；

基于各组样本数据中第一角度与差模和模比的对应关系拟合得到第一函数关系，第一函数反应第一角度与差模和模比之间的函数关系。

其进一步的技术方案为，每组样本数据中的样本目标的目标来向指示样本目标的俯仰角和方位角，则基于样本数据拟合得到第二函数关系，包括：

对于每个样本数据，计算样本数据的四个原始天线波束的和波束和差波束并分别对和波束和差波束进行不同的波束运算得到四个偏轴正交波束；

根据其中一组对角的两个偏轴正交波束与和波束确定第一参数，根据另外一组对角的两个偏轴正交波束与和波束确定第二参数；

基于样本数据拟合得到方位角与第一参数之间的函数关系以及拟合得到俯仰角与第二参数之间的函数关系，得到第二函数关系。

其进一步的技术方案为，基于样本数据拟合得到方位角与第一参数之间的函数关系以及拟合得到俯仰角与第二参数之间的函数关系，包括：按照α＝b0+b1·k1的形式拟合得到方位角与第一参数之间的函数关系，按照β＝c0+c1·k2的形式拟合得到俯仰角与第二参数之间的函数关系，其中α是方位角，b0、b1是系数，k1是第一参数，β是俯仰角，c0、c1是系数，k2是第二参数。

其进一步的技术方案为，根据其中一组对角的两个偏轴正交波束与和波束确定第一参数，根据另外一组对角的两个偏轴正交波束与和波束确定第二参数，包括：

确定第一参数为确定第二参数为其中，b1和b3是一组对角的两个偏轴正交波束，b2和b4是另一组对角的两个偏轴正交波束，m1是和波束，符号||表示波束的幅度。

其进一步的技术方案为，计算样本数据的四个原始天线波束的和波束和差波束并分别对和波束和差波束进行不同的波束运算得到四个偏轴正交波束，包括：

确定和波束为m1＝p1-j*p2-p3+j*p4、差波束为m2＝p1-p2+p3-p4，p1、p2、p3、p4分别为四个原始天线波束；

确定四个偏轴正交波束b1、b2、b3、b4分别为其中，b1和b3为一组对角的两个偏轴正交波束，b2和b4为另一组对角的两个偏轴正交波束。

本发明的有益技术效果是：

本申请公开了一种四臂螺旋天线数据拟合测角方法，该方法采用数据拟合算法来降低查表法带来的内存占用过大，查表效率低下的问题；拟合算法可以方便的得到测角结果，同时存储的参数很少，节约了内存开销，解决目前查表法结构带来的两大弊端，可广泛应用在被动式导引头天线中，采用四臂螺旋天线测角，频带范围可从580m到2g。

附图说明

图1是四天线全向振幅单脉冲测量原理框图。

图2是相邻天线的振幅方向图。

图3是本申请的四臂螺旋天线数据拟合测角方法的方法流程图。

具体实施方式

下面结合附图对本发明的具体实施方式做进一步说明。

本申请公开了一种四臂螺旋天线数据拟合测角方法，请参考图3，该方法包括如下步骤：

步骤s1，利用基于四臂螺旋天线的被动测向系统对不同角度处的样本目标进行测向，在每一次测向中确定样本目标在天线坐标系中的目标来向以及对应的通过四臂螺旋天线获取到的四个原始天线波束p1、p2、p3、p4得到一组样本数据。在本申请中，样本目标的目标来向指示该样本目标的俯仰角β和方位角α，还指示样本目标的第一角度θ和第二角度φ，第一角度是目标来向与天线坐标系的水平面也即xy平面之间的夹角，第二角度是目标来向在水平面也即xy平面上的投影与预定指向之间的夹角，该预定指向预先自定义，通常取天线坐标系的x轴或y轴的方向作为该预定指向。

(α，β)与(θ，φ)可以通过坐标转换进行互相转换得到，因此样本目标的目标来向实际可以仅包括(α，β)与(θ，φ)中的一组角度，另一组角度可以相应转换得到。或者目标来向实际可以同时包括(α，β)与(θ，φ)，则以此情况为例，每一次测向得到的一组样本数据可以表示为{(α,β),(θ，φ)，(p1,p2,p3,p4)}。

步骤s2，基于样本数据拟合得到第一函数关系，第一函数关系是第一角度θ与四个原始天线波束之间的函数关系。可选的在本申请中，第一函数关系并不直接反应第一角度θ与四个原始天线波束之间的函数关系，而是反应第一角度θ与差模和模比之间的函数关系，也即f1()为第一函数关系，其中，m1为和波束，m2为差波束，符号||表示波束的幅度。因此在拟合得到第一函数关系时，首先对于每个样本数据，计算样本数据的四个原始天线波束p1、p2、p3、p4的和波束m1和差波束m2，计算方法为m1＝p1-j*p2-p3+j*p4，m2＝p1-p2+p3-p4，然后计算差波束m2与和波束m1的比值得到差模和模比然后基于各组样本数据中第一角度θ与差模和模比的对应关系拟合得到第一函数关系f1()。

步骤s3，基于样本数据拟合得到第二函数关系，第二函数关系是基于目标来向确定的俯仰角β和方位角α与四个原始天线波束之间的函数关系。同样的，本申请并不直接确定β、α与四个原始天线波束之间的函数关系，而是首先对于每个样本数据，计算样本数据的四个原始天线波束p1、p2、p3、p4的和波束m1和差波束m2，计算方法如上述步骤s2。然后分别对和波束m1和差波束m2进行不同的波束运算得到四个偏轴正交波束b1、b2、b3、b4，计算方法为：

其中，b1和b3为一组对角的两个偏轴正交波束，b2和b4为另一组对角的两个偏轴正交波束。根据其中一组对角的两个偏轴正交波束b1和b3与和波束m1确定第一参数k1，根据另外一组对角的两个偏轴正交波束b2和b4与和波束m1确定第二参数k2，具体的：第一参数为确定第二参数为由此可以处理每组样本数据得到目标来向确定的俯仰角β和方位角α及其对应的第一参数k1和第二参数k2。

然后基于样本数据拟合得到方位角α与第一参数k1之间的函数关系以及拟合得到俯仰角β与第二参数k2之间的函数关系，得到第二函数关系。本申请采用多项式拟合，也即按照α＝b0+b1·k1的形式拟合得到方位角α与第一参数k1之间的函数关系，按照β＝c0+c1·k2的形式拟合得到俯仰角β与第二参数k2之间的函数关系，b0、b1是系数，c0、c1是系数。

步骤s4，利用基于四臂螺旋天线的被动测向系统获取待测目标的四个原始天线波束。利用待测目标的四个原始天线波束基于第一函数关系得到第一角度第一预估值，与上述拟合过程类似，先由四个原始天线波束处理得到差模和模比然后代入第一函数关系得到对应的第一角度第一预估值θ1。

步骤s5，利用待测目标的四个原始天线波束基于第二函数关系得到俯仰角预估值β0和方位角预估值α0，与上述拟合过程类似，先由四个原始天线波束处理得到第一参数k1和第二参数k2，然后代入上述第二函数关系得到俯仰角预估值β0和方位角预估值α0。

基于俯仰角预估值β0和方位角预估值α0得到第一角度第二预估值θ2和第二角度预估值φ0，按照如下公式得到：确定第一角度第二预估值为θ2＝cos^-1(cos(β0)cos(α0))，确定第二角度预估值为φ0＝tan^-1(tan(β0)/sin(α0))

步骤s6，根据第一角度第一预估值θ1、第一角度第二预估值θ2和第二角度预估值φ0修正俯仰角预估值β0和方位角预估值α0得到待测目标的俯仰角和方位角。具体的：

(1)当第一角度第一预估值θ1和第一角度第二预估值θ2之间的差值达到预定阈值t时，利用第一角度第一预估值θ1和第二角度预估值φ0修正俯仰角预估值β0和方位角预估值α0得到待测目标的俯仰角和方位角。该预定阈值为自定义值，本申请较为典型的将其取值为0.02。

利用θ1和φ0修正得到俯仰角和方位角的做法为：修正俯仰角预估值为β＝tan^-1(cosφ0tanθ1)得到待测目标的俯仰角，修正方位角预估值为α＝sin^-1(sinφ0sinθ1)得到待测目标的方位角。

(2)当第一角度第一预估值θ1和第一角度第二预估值θ2之间的差值未达到预定阈值t时，直接将步骤s5得到的俯仰角预估值β0作为待测目标的俯仰角，将方位角预估值α0作为待测目标的方位角。

以上所述的仅是本申请的优选实施方式，本发明不限于以上实施例。可以理解，本领域技术人员在不脱离本发明的精神和构思的前提下直接导出或联想到的其他改进和变化，均应认为包含在本发明的保护范围之内。