磁性线性位置感应器的制作方法

1.本发明涉及一种位置感应器，特别涉及一种磁性线性位置感应器。


背景技术：

2.参见图1所示，现有获得一磁性角度型感应元件s(例如amr、hall、tmr
…
)的侦测距离的一种方式是令磁性角度型感应元件s感应沿一直线行程p1运动的磁铁m的磁场，使产生与磁铁m的一移动距离相关的一正弦波信号和一余弦波信号并输出至一信号处理器10，该信号处理器10将该正弦波信号和余弦波信号数字化为如图1所示的由多个正弦信号值usin形成的数字化正弦波信号sin以及如图1示的由多个余弦信号值ucos形成的数字化余弦波信号cos，并对该等正弦信号值usin和该等余弦信号值ucos进行反正切函数(arctan)的二阶导数(atan2)运算，即atan2(usin/ucos)，可求得多个曲率值，且该等曲率值形成如图1所示的一曲率曲线c1，该曲率曲线c1中的一有效线段l1上的每一点的曲率值对应一侦测距离，且因为该有效线段l1的曲率值范围只有从0.2～1.2，代表磁性角度型感应元件s的一有效侦测距离并不长，例如图1所示的侦测距离只有6mm，因此，假设需要侦测的长度是6mm的6倍，则至少需要并列6颗磁性角度型感应元件s同时进行侦测。


技术实现要素：

3.本发明的目的是提供一种磁性线性位置感应器，其能增长其中的磁性角度型感应元件的侦测距离，进而减少磁性角度型感应元件的使用数量。
4.本发明提供一种磁性线性位置感应器，用以侦测沿一直线行程往复移动的一磁铁的位置，并包括一磁性角度型感应元件及一处理单元；该磁性角度型感应元件设于该直线行程的一侧以感应该磁铁的磁场并输出一正弦信号和一余弦信号；该处理单元与该磁性角度型感应元件电连接，以接收该正弦信号和该余弦信号，并将该正弦信号和该余弦信号数字化为一正弦信号值和一余弦信号值，且对减去一第一预设值的该正弦信号值和减去一第二预设值的该余弦信号值进行反正切函数的二阶导数运算，即atan2(减去该第一预设值的该正弦信号值/减去该第二预设值的该余弦信号值)，以获得一曲率值；该处理单元将该曲率值输入一与该磁性角度型感应元件特性相关的数学模型，以求得该磁性角度型感应元件与该磁铁的一相对距离；该数学模型是由一多项式方程式及一曲率值范围建构以拟合该磁性角度型感应元件的一特性曲线，其中i等于1,2,3
…
n，y
i
是该相对距离，x
i
是该曲率值，β0～β
m
是该磁性角度型感应元件的系数，该曲率值范围的最小值和最大值是该特性曲线两端的曲率值。
5.在本发明的一些实施态样中，该数学模型是于该磁性线性位置感应器的一校正程序中建立，在该校正程序中，该磁铁沿该直线行程移动，一信号处理装置令该处理单元以一取样频率要求该磁性角度型感应元件回传当下产生的该正弦信号和该余弦信号直到该磁铁走完该直线行程；该处理单元将该等正弦信号和该等余弦信号数字化后输出至该信号处
理装置，该信号处理装置根据该直线行程的长度和该取样频率，获得该磁铁在该直线行程中每一个取样点的位置与数字化的该等正弦信号值和该等余弦信号值的对应关系，该信号处理装置将该等正弦信号值减去一第一预设值，并将该等余弦信号值减去一第二预设值，该信号处理装置对减去该第一预设值的该等正弦信号值和减去该第二预设值的该等余弦信号值进行反正切函数的二阶导数(atan2)运算，即atan2(减去该第一预设值的该正弦信号值/减去该第二预设值的该余弦信号值)，而获得相对应的多个曲率值，该等曲率值构成一曲率曲线，且该信号处理装置以该曲率曲线中的一有效线段作为该磁性角度型感应元件的该特性曲线，并根据该特性曲线决定该磁性角度型感应元件的一有效侦测距离以及相对应的一曲率值范围，且借由曲线拟合和线性回归分析决定该多项式方程式的m值以及β0～β
m
的值，且该信号处理装置将该多项式方程式及该曲率值范围写入该处理单元中作为该特性曲线的该数学模型。
6.在本发明的一些实施态样中，该第一预设值是该等正弦信号值中的最大值与最小值之合的二之一；该第二预设值是该等余弦信号值中的最大值与最小值之合的二之一。
7.在本发明的一些实施态样中，m为6。
8.在本发明的一些实施态样中，该磁性角度型感应元件具有两个相差45
°
的磁阻电桥，其中一磁阻电桥感应该磁铁的磁场并产生一正弦波信号，其中另一磁阻电桥感应该磁铁的磁场并产生一与该正弦波信号的相位差45
°
的余弦波信号。
9.在本发明的一些实施态样中，该处理单元在判断为该曲率值在该曲率值范围内的情况下才将该曲率值输入该数学模型。
10.本发明的有益效果在于：借由该处理单元的该数学模型拟合该磁性角度型感应元件的特性曲线，该处理单元只需将该磁性角度型感应元件传来的该正弦信号和该余弦信号数字化后，对减去第一预设值的该正弦信号值和减去第二预设值的该余弦信号值进行atan2(减去该第一预设值的该正弦信号值/减去该第二预设值的该余弦信号值)运算获得一曲率值后，将该曲率值输入该数学模型，即可通过简单的一元m次多项式方程式快速求得该磁性角度型感应元件与该磁铁的一相对距离；而且该数学模型所拟合的该特性曲线决定该磁性角度型感应元件的一有效侦测距离以及相对应的一曲率值范围，而在校正程序中，借由将该磁性角度型感应元件感应获得的该等正弦信号值和该等余弦信号适当平移后再对其进行反正切函数(arctan)的二阶导数(atan2)运算，能使该有效侦测距离增长，而减少磁性角度型感应元件的使用数量并使该磁性线性位置感应器的侦测距离变长。
附图说明
11.图1说明现有获得磁性角度型感应元件的侦测距离的一种方法。
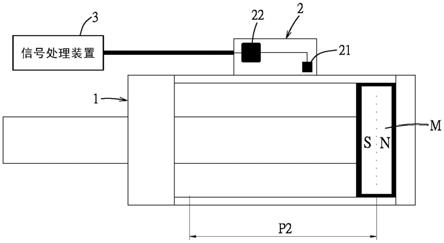
12.图2说明本发明磁性线性位置感应器的一实施例包含的元件及其应用例。
13.图3是本实施例的磁性角度型感应元件包含的细部电路示意图。
14.图4是经由本实施例的处理单元数字化后的数字化正弦波信号sin和数字化余弦波信号cos的波形示意图。
15.图5说明将图4的数字化正弦波信号sin和数字化余弦波信号cos分别向下平移一第一预设值和一第二预设值。
16.图6说明对图5所示的正弦波信号sin’和余弦波信号cos’进行反正切函数(arctan)的二阶导数(atan2)运算以获得相对应的多个曲率值，该等曲率值构成一曲率曲线c2。
17.图7说明将图6所示的曲率曲线c2的有效线段l2的x轴数据与y轴数据置换，而变成置换后有效线段l2’。
具体实施方式
18.下面结合附图及实施例对本发明进行详细说明：
19.在本发明被详细描述之前，应当注意在以下的说明内容中，类似的元件是以相同的编号来表示。
20.参阅图2所示，是本发明磁性线性位置感应器的一实施例，其用以侦测沿一直线行程p2往复移动的一磁铁m的位置，例如该磁铁m是设于一气缸1内的一活塞，且该直线行程p2是该活塞在该气缸1内往复运动的活塞行程；本实施例的磁性线性位置感应器2主要包括一磁性角度型感应元件21及一处理单元22，例如一微处理器或一微控制器(mcu)。该磁性角度型感应元件21设于该直线行程p2的一侧，例如该气缸1的外壁面，以感应该磁铁m的磁场并输出模拟的一正弦信号和一余弦信号；该处理单元22与该磁性角度型感应元件21电连接，以接收该正弦信号和该余弦信号，且该处理单元22中存有一与该磁性角度型感应元件21特性相关的一数学模型，该数学模型是由一多项式方程式及一曲率值范围建构以拟合该磁性角度型感应元件21的一特性曲线，其中i＝1,2,3
…
n，y
i
代表该磁性角度型感应元件21与该磁铁m的一相对距离，x
i
代表一曲率值，β0～β
m
代表该磁性角度型感应元件21的系数，该曲率值范围的最小值和最大值是该特性曲线两端的曲率值。
21.具体而言，该数学模型是在该磁性线性位置感应器2的一校正程序中建立，由于每一磁性线性位置感应器2中的该磁性角度型感应元件21的特性都不相同，因此在该磁性线性位置感应器2出厂之前，该磁性线性位置感应器2需先经过校正以找到符合该磁性角度型感应元件21特性的该数学模型；且如图3所示，该磁性角度型感应元件21(例如amr、hall、tmr
…
)内具有两个相位差45
°
(即夹45
°
角)的磁阻电桥(bridge)211、212；在校正程序中，如图2所示，会使磁铁m从该直线行程p2的远离该磁性角度型感应元件21的一端朝该磁性角度型感应元件21移动，并通过该磁性角度型感应元件21后朝远离该磁性角度型感应元件21方向移动至该直线行程p2的另一端，在此过程中，这两个磁阻电桥211、212会持续感应磁铁m的磁场而产生相位差45
°
的一正弦波信号sin和一余弦波信号cos。
22.同时，一信号处理装置3，例如但不限于一个人计算机，令该处理单元22以一取样频率(例如10次/秒)要求该磁性角度型感应元件21回传当下产生的该正弦信号(即该正弦波信号sin的某一点的值，模拟电压值)和该余弦信号(即该余弦波信号cos的某一点的值，模拟电压值)，直到该磁铁m走完该直线行程p2，借此，该磁性角度型感应元件21每秒将回传10笔正弦信号和10笔余弦信号给该处理单元22，且该处理单元22将收到的该等正弦信号和该等余弦信号数字化后输出至该信号处理装置3。该等正弦信号值usin和该等余弦信号值ucos的数字化数值可对照图4左边纵轴所标示的数值。
的多项式方程式例如采用多项式拟合(polynomial fitting)，以一元m次多项式回归方程式来拟合该置换后有效线段l2’，并以如下所示的矩阵解多项式回归方程式：
[0028][0029]
其中i＝1,2,3
…
n，y1～y
n
代表该100个距离值，x1～x
n
代表该100个曲率值，β0～β
m
是系数，且由于每个该磁性角度型感应元件21的特性不同，因此其系数β0～β
m
亦不相同，所以借由上述矩阵运算，可以找出该磁性角度型感应元件21的该等系数β0～β
m
的值，以及决定要采用的拟合该置换后有效线段l2’的多项式方程式。例如，本实施例可以应用matlab提供的polyfit指令找出上述一元m次多项式方程式的最佳参数以及最符合该置换后有效线段l2’的方程式。
[0030]
举例来说，借由polyfit指令将上述已知的该100笔曲率值(x1～x
n
)与相对应的该100笔距离值(y1～y
n
)分别代入1元1次～1元8次共8个多项式方程式中，将求得这8个多项式方程式各自的最佳系数及其与该置换后有效线段l2’的拟合结果，且从这8个多项式方程式中发现一元6次多项式方程式拟合该置换后有效线段l2’的结果最佳时，该信号处理装置3则采用具有最佳拟合结果的一元6次多项式方程式，该方程式例如为y＝2.4431x6‑
8.2418x5+15.967x4‑
10.349x3+7.6091x2+1.567x+1.0009，并以该一元6次多项式方程式作为该数学模型；其中y代表磁铁m与该磁性角度型感应元件21的距离值，x代表曲率值。然后，该信号处理装置3将该一元6次多项式方程式及该曲率值范围写入该处理单元22中作为该数学模型，即完成该校正程序。
[0031]
借此，当该磁性线性位置感应器2实际应用于例如图2所示的气缸1时，该处理单元22接收到该磁性角度型感应元件21传来的模拟的该正弦信号和该余弦信号时，该处理单元22将该正弦信号和该余弦信号数字化为一正弦信号值和一余弦信号值，且将该正弦信号值减去该第一预设值以及将该余弦信号值减去该第二预设值后，对减去该第一预设值的该正弦信号值和减去该第二预设值的该余弦信号值进行反正切函数(arctan)的二阶导数(atan2)运算，即atan2(减去该第一预设值的该正弦信号值/减去该第二预设值的该余弦信号值)，以获得一曲率值；然后，该处理单元22在判断为该曲率值是在该曲率值范围内时，将该曲率值代入该数学模型中，即可借由该一元6次多项式方程式求得一距离值，该距离值即代表该磁性角度型感应元件21与该磁铁m的一相对距离；然后，该处理单元22可以直接输出该距离值供后端应用，或者将该距离值转成相对应的一模拟信号，例如模拟电压(比如1～5v其中的一电压值)或模拟电流(比如4～20ma其中的一电流值)再输出给后端应用。
[0032]
综上所述，上述实施例借由该处理单元中的该数学模型拟合该磁性角度型感应元
件21的特性曲线，该处理单元只需将该磁性角度型感应元件21传来的该正弦信号和该余弦信号数字化后，对减去第一预设值的该正弦信号值和减去第二预设值的该余弦信号值进行atan2(减去该第一预设值的该正弦信号值/减去该第二预设值的该余弦信号值)运算，获得对应的一曲率值后，将该曲率值输入计算距离的该数学模型，即可通过简单的一元m次多项式方程式快速求得该磁性角度型感应元件21与该磁铁m的一相对距离；并且，该数学模型所拟合的该特性曲线决定该磁性角度型感应元件21的一有效侦测距离以及相对应的一曲率值范围，而本实施例在校正程序中，借由将该磁性角度型感应元件21感应获得的该等正弦信号值和该等余弦信号适当平移后再对其进行反正切函数(arctan)的二阶导数(atan2)运算，能使该有效侦测距离增长，而达到减少磁性角度型感应元件21的使用数量并使该磁性线性位置感应器2的侦测距离变长的功效与目的。
[0033]
以上所述仅为本发明较佳实施例，然其并非用以限定本发明的范围，任何熟悉本项技术的人员，在不脱离本发明的精神和范围内，可在此基础上做进一步的改进和变化，因此本发明的保护范围当以本申请的权利要求书所界定的范围为准。