一种快速收敛的超短脉冲波形与相位重建方法

1.本发明涉及超短脉冲测量方法，特别是一种能够快速收敛的超短脉冲波形和相位重建方法。


背景技术：

2.脉冲激光的发展对激光测量技术提出了更高要求，在许多应用场景中，需要获得脉冲的频谱分布及相位信息以进一步研究其传输特性及与物质相互作用的机理，因此超短脉冲的测量十分重要且具有挑战性。
3.目前最实用、最可靠、最成熟的方法是频率分辨光学开关法(frog)，可以利用各种非线性过程产生不同类型的行迹(trace)图进行测量，但是frog在传统脉冲波形与相位的重建算法上并不理想，现有算法仍存在许多限制因素，如收敛停滞、重建速度等。2016年pavel sidorenko和oren lahav等人提出利用相干衍射成像中ptychography恢复算法对超短脉冲波形与相位进行重建，该方法具有超高分辨率、很好的抗噪性和鲁棒性，但在实际超短脉冲强度和相位重建时，由于其速度比较慢，对超短脉冲波形与相位的测量具有滞后性，无法做到实时测量，还可能陷入收敛停滞，无法得到最终正确的结果，给超短脉冲的测量及进一步研究其其传输特性及与物质相互作用的过程带来了很大的麻烦，因此对基于ptychography的恢复算法快速准确的测量超短脉冲的研究具有十分重要的意义。


技术实现要素：

4.针对上述超短脉冲波形与相位重建方法上的缺陷，提出一种能够快速收敛的超短脉冲波形和相位重建方法，对于frog装置采集的关于频率和延时的二维trace图，利用频率边缘函数和脉冲功率谱的关系及脉冲时域连续性可以计算出脉冲准确的强度，脉冲在重建过程中更新强度和相位，比原来的假设固定强度和随机相位的初始猜测值，有准确的强度信息能够更快收敛至好的最终结果。对采集的二维trace图进行多重网格预处理，将m
×
n的trace图邻近插值成m/a
×
n/a和m/b
×
n/b大小，对不同矩阵大小进行处理时，迭代次数可以较少，缩短迭代过程中猜测脉冲趋近待测脉冲的时间。所以，利用准确强度加随机相位的初始猜测和对采集到的二维trace图进行多重网格预处理，可以提高超短脉冲波形与相位重建的收敛速度，尤其是对时间带宽积比较大的复杂脉冲，达到对超短脉冲实时准确的测量。
5.为实现上述发明目的，本发明的技术解决方案如下：
6.一种快速收敛的超短脉冲波形与相位重建方法，其特征在于包括以下步骤：
7.步骤1)，超短脉冲的初始猜测优化：
8.采集关于频率和延时的矩阵大小为m
×
n的二维trace图，计算该二维trace图的频率边缘函数，利用频率边缘函数和脉冲的时域连续性计算待测脉冲功率谱，即可得到待测脉冲强度；
9.步骤2)，对二维trace图进行多重网格预处理：
10.对m
×
n的二维trace图邻近插值成m/a
×
n/a和m/b
×
n/b的二维trace图，其中a和b
32.式中，f表示傅里叶变换，e
j,k
(t
‑
τ)表示延时脉冲时域表达式，j为当前迭代次数；；
[0033]3‑
3)利用初始采集的二维trace图i
sig
(ω,τ)进行更新，更新公式为：
[0034][0035]
式中，ψ
j,k
(t,τ)＝e
j,k
(t)e
j,k
(t
‑
τ)，ψ
j,k
(ω,τ)＝f(ψ
j,k
(t,τ))；
[0036]3‑
4)基于ptychography的恢复算法脉冲强度与相位的迭代过程公式为：
[0037][0038]
其中，ξ为更新系数，为e
j,k
(t
‑
τ)的共轭形式，在每次迭代中e
j+1,k
(t)将对e
j,k
(t)进行更新，返回步骤3
‑
2)，当j＝β3时迭代完成；
[0039]3‑
5)计算并行迭代完成后得到的所有重建脉冲的二维trace图与采集的m
×
n的二维trace图的误差g
k
，公式如下：
[0040][0041]
式中，k＝1,2,
…
,α3，比较g
k
大小，从α3个输出重建脉冲中选出误差最小的α2个重建脉冲；
[0042]
其次，将这α2个重建脉冲设为对m/a
×
n/a二维trace图迭代处理的初始猜测脉冲，重复步骤3
‑
2)
‑3‑
4)，直至j＝β2时迭代完成，得到α2个重建脉冲，重复步骤3
‑
5)，此时k＝1,2,
…
,α2，比较g
k
大小，从α2个重建脉冲中选出误差最小的α1个重建脉冲；
[0043]
最后，将这α1个重建脉冲设为对采集的m
×
n二维trace图迭代处理的初始猜测脉冲，重复步骤3
‑
2)
‑3‑
4)，直至j＝β1时迭代完成，得到α1个重建脉冲，重复步骤3
‑
5)，此时k＝1,2,
…
,α1，比较g
k
大小，选出误差最小的重建脉冲即最终重建的脉冲，包含脉冲波形与相位信息。
[0044]
本发明的技术效果如下：
[0045]
与传统超短脉冲波形与相位重建算法对比，此算法不需要对脉冲单独测功率谱，可以直接从采集到的二维trace图中直接计算的到准确的强度信息，将m
×
n图谱邻近插值为更小的m/a
×
n/a图谱和m/b
×
n/b图谱，总迭代次数大大减小，确保了较快的恢复速度。更新迭代时使用基于ptychography的脉冲重建算法，对不完整的二维n
×
n图谱也能很好的重建出原始脉冲，结合对二维trace图的多重网格预处理和准确度较高的初始猜测，即保证了重建速度又保证了准确性，能够实现对超短脉冲的实时测量，还具有很好的抗噪性，对采集的含有噪声的二维trace图也能很好的重建效果。
附图说明
[0046]
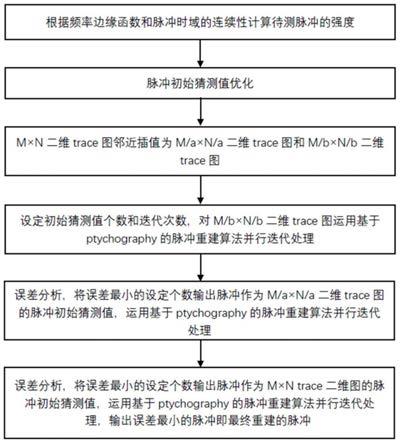
图1为本发明方法具体流程图；
[0047]
图2为采集到的shg
‑
frog二维trace图；
[0048]
图3为根据采集的二维trace图计算的待测脉冲时域波形；
[0049]
图4为利用优化后脉冲初始猜测和对二维trace图多重网格预处理后运用
ptychography恢复算法重建的脉冲时域的强度和相位；
[0050]
图5为利用优化后的脉冲初始猜测和对二维trace图多重网格预处理后运用ptychography恢复算法重建的脉冲频域的强度和相位。
具体实施方式
[0051]
下面结合实施案例和附图对本发明进一步说明，但不应以此限制本发明的保护范围。
[0052]
如图1所示，本发明公开了一种快速收敛的超短脉冲波形与相位重建方法，包括以下步骤：
[0053]
步骤1)，超短脉冲的初始猜测优化：
[0054]
采集关于频率和延时的矩阵大小为m
×
n的二维trace图，计算该二维trace图的频率边缘函数，利用频率边缘函数和脉冲的时域连续性计算待测脉冲功率谱，即可得到待测脉冲强度；
[0055]
步骤2)，对二维trace图进行多重网格预处理：
[0056]
对m
×
n的二维trace图邻近插值成m/a
×
n/a和m/b
×
n/b的二维trace图，其中a和b为大于等于2的正整数，且b>a；
[0057]
步骤3)，按矩阵大小依次从小到大对每个二维trace图采用ptychography迭代法对脉冲波形与相位进行重建。
[0058]
所述的步骤1)超短脉冲的初始猜测优化，具体步骤如下：
[0059]
首先，计算频率边缘函数m(ω)，公式如下：
[0060]
m(ω)＝∫i
sig
(ω,τ)dτ
[0061]
式中，ω为频率，τ为时间延时，i
sig
(ω,τ)为采集的二维trace图表达式；
[0062]
频率边缘函数和脉冲功率谱的关系为：
[0063]
f
‑1{m(ω)}＝(f
‑1{s(ω)})2＝s(t)2[0064]
式中，s(ω)为功率谱，f
‑1表示傅里叶逆变换，s(t)为s(ω)逆变换，
[0065]
然后，根据脉冲时域连续性，对于t和t+1时间点，s(t)和s(t+1)符号应相同，依次对比s(t)和s(t+1)的符号，计算出s(t)，从而得到脉冲功率谱s(ω)，则待测脉冲频谱强度
[0066]
所述的步骤2)，对二维trace图进行多重网格预处理，具体步骤如下：
[0067]
首先，对m
×
n大小的trace图中频率轴m个坐标点和延时轴n个坐标点分别等间隔取m/a和n/a个点，利用已知m
×
n大小的二维trace图对m/a
×
n/a坐标进行邻近插值，得到m/a
×
n/a二维trace图；
[0068]
其次，对m
×
n大小的trace图中频率轴m个坐标点和延时轴n个坐标点分别等间隔取m/b和n/b个点，利用已知m
×
n大小的二维trace图对m/b
×
n/b坐标进行邻近插值，得到m/b
×
n/b二维trace图；
[0069]
得到的m/a
×
n/a二维trace图和m/b
×
n/b二维trace图都包含了初始m
×
n二维trace图中部分关于频率和延时的强度自相关谱信息。
[0070]
所述的步骤3)，按矩阵大小依次从小到大对每个二维trace图采用ptychography迭代法对脉冲波形与相位进行重建。具体步骤如下：
[0071]
先对m
×
n二维trace图设定α1个初始猜测值和β1迭代次数，对m/a
×
n/a二维trace图设定α2个初始猜测值和β2迭代次数，对m/b
×
n/b二维trace图设定α3个初始猜测脉冲和β3迭代次数，其中α3>α2>α1。先对m/b
×
n/b二维trace图运用脉冲波形与相位重建算法并行迭代处理，脉冲重建过程为：
[0072]3‑
1)确定α3个初始猜测脉冲时域表达式e
k
(t)，公式如下：
[0073][0074]
式中，为随机相位，k＝1,2,
…
,α3，对α3个初始猜测脉冲并行运行以下步骤；
[0075]3‑
2)计算重建脉冲的二维trace图i
′
sig,k
(ω,τ)，公式如下：
[0076]
i
′
sig,k
(ω,τ)＝|f(e
j,k
(t)e
j,k
(t
‑
τ))|2[0077]
式中，f表示傅里叶变换，e
j,k
(t
‑
τ)表示延时脉冲时域表达式，j为当前迭代次数；；
[0078]3‑
3)利用初始采集的二维trace图i
sig
(ω,τ)进行更新，更新公式为：
[0079][0080]
式中，ψ
j,k
(t,τ)＝e
j,k
(t)e
j,k
(t
‑
τ)，ψ
j,k
(ω,τ)＝f(ψ
j,k
(t,τ))；
[0081]3‑
4)基于ptychography的恢复算法脉冲强度与相位的迭代过程公式为：
[0082][0083]
其中，ξ为更新系数，为e
j,k
(t
‑
τ)的共轭形式，在每次迭代中e
j+1,k
(t)将对e
j,k
(t)进行更新，返回步骤3
‑
2)，当j＝β3时迭代完成；
[0084]3‑
5)计算并行迭代完成后得到的所有重建脉冲的二维trace图与采集的m
×
n的二维trace图的误差g
k
，公式如下：
[0085][0086]
式中，k＝1,2,
…
,α3，比较g
k
大小，从α3个输出重建脉冲中选出误差最小的α2个重建脉冲；
[0087]
其次，将这α2个重建脉冲设为对m/a
×
n/a二维trace图迭代处理的初始猜测脉冲，重复步骤3
‑
2)
‑3‑
4)，直至j＝β2时迭代完成，得到α2个重建脉冲，重复步骤3
‑
5)，此时k＝1,2,
…
,α2，比较g
k
大小，从α2个重建脉冲中选出误差最小的α1个重建脉冲；
[0088]
最后，将这α1个重建脉冲设为对采集的m
×
n二维trace图迭代处理的初始猜测脉冲，重复步骤3
‑
2)
‑3‑
4)，直至j＝β1时迭代完成，得到α1个重建脉冲，重复步骤3
‑
5)，此时k＝1,2,
…
,α1，比较g
k
大小，选出误差最小的重建脉冲即最终重建的脉冲，包含脉冲波形与相位信息。
[0089]
下面是本发明一个实施例的参数：
[0090]
图2为利用shg
‑
frog装置采集的皮秒量级待测脉冲的二维trace图，其中心波长为
1026nm，时间分辨率为80fs，波长分辨率为0.08nm，二维trace图矩阵大小为256
×
256，即m＝n＝256，且a＝2，b＝4。对二维trace图进行多重网格预处理后设定的脉冲初始猜测个数和迭代次数，α3＝24，α2＝＝12，α1＝4，β3＝15，β2＝15，β1＝200。图3为通过256
×
256二维trace图计算得到的待测脉冲时域强度，对于64
×
64二维trace图运行重建算法时，α3个脉冲初始猜测为该时域强度加上随机相位。如图4和图5分别为利用优化后的脉冲初始猜测和对二维trace图多重网格预处理后运用ptychography恢复算法重建的脉冲时域和频域的强度和相位。同时，能够得出相应脉冲时域宽度和频谱宽度分别为0.436ps和10.212nm。
[0091]
实验表明，利用frog超短脉冲单次测量装置采集的关于频率和延时的二维trace图计算的准确强度加随机相位的初始猜测，和对该二维trace图进行多重网格预处理，可以缩小脉冲重建时间和提高脉冲重建准确度，本发明方便、快捷，能够实现快速收敛的超短脉冲测量。