一种基于图优化的UWB/IMU的室内移动机器人协同定位方法

本发明涉及一种室内移动机器人定位方法属于机器人领域，属于无线传感器网络的定位技术领域。

背景技术：

超宽带(uwb)定位技术其本质上属于无线传感器网络的定位技术，在室内定位中，uwb定位技术因其定位精度较高，设备价格低廉，抗干扰能力强等特点而得到广泛应用，目前uwb定位技术主要采用tdoa测距算法，rssi测距算法等各种算法进行定位距离估算，但tdoa，rssi测距算法误差较大，且在机器人运动过程中，uwb无法评估机器人自身姿态，本发明利用uwb系统，imu惯性测量单元，通过imu数据初步校验uwb数据，判断数据是否受到nlos影响，使用柯西鲁棒核函数，列文伯格-马夸尔特算法优化机器人当前时刻的位姿。大大提高了使用uwb在非视距情况下，进行机器人定位时机器人定位位姿不准的问题。得到在视距情况下比单一uwb定位更加精确的定位效果

技术实现要素：

为了解决上述问题，本发明提出了一种基于图优化的uwb/imu的室内移动机器人定位方法。

为了实现上述技术目的，本发明的技术方案为：

一种基于图优化的uwb/imu的室内移动机器人协同定位方法，实现该方法的系统包括机器人运动控制系统、机器人通讯系统、uwb系统和imu惯性测量单元；所述uwb系统包括2个及以上标签与imu，4个及以上基站，所述标签将接收基站所发送的信号，通过tof的方法测得标签与基站之间的距离。所述标签与imu皆搭设于机器人。本发明利用uwb系统，imu惯性测量单元，通过imu数据初步校验uwb数据，判断数据是否受到nlos影响，使用柯西鲁棒核函数，列文伯格-马夸尔特算法优化机器人当前时刻的位姿。大大提高了使用uwb在非视距情况下，进行机器人定位时机器人定位位姿不准的问题。得到在视距情况下比单一uwb定位更加精确的定位效果。

包括以下步骤：

(1)建立机器人uwb/imu的测量模型；

(2)初步校验uwb数据，判断数据是否受到nlos影响。

(3)构建机器人位姿优化图，推导误差函数，将机器人位置优化问题转化为位姿图优化问题。

(4)使用柯西鲁棒核函数，列文伯格-马夸尔特算法，优化机器人当前时刻的位姿；

在步骤(1)中，所述uwb测量模型如下：

其中l1，l2，l3....ln为各基站到机器人的距离，(x1,y1,z`1),(x2,y2,z2),(x3,y3,z3).....(xn,yn,zn)表示为基站坐标，(xu,yu,zu)为机器人位置；

在步骤(1)中，所述imu测量模型如下：

为机器人在j,i时刻的位置，为机器人j.i时刻在世界坐标系下的速度，g^w为世界坐标系下，机器人的重力加速度。δt为两次采样时间间隔。为imu预积分量。为imu加速度计，陀螺仪的整体偏移量，为整体偏移使用随机游走模型的参数变量。a,w为使用中值滤波法计算得到的机器人当前时刻线加速度与角速度。

步骤(2)中，初步校验uwb数据，判断数据是否受到nlos影响。在k到k+1时刻有：

其中xk,xk-1为机器人在k，k-1时刻的位姿，因此可令

对rk进行检验，若则可认为uwb出现了异常测量值。

丢弃该测量值，记录uwb中有效测量的数量。

若此时有效数量m＜2，则该时刻的uwb帧无法作为定位使用，利用imu对该时刻进行保持。

若m＝2，由于室内环境中，地面相对平坦，可将z轴坐标看做一个常数，可令zk＝zk-1。

步骤(3)中，依照步骤2中的测量模型，构建误差函数

其中ei,eu,eui分别为imu测量残差，uwb测量残差，以及imu到uwb坐标转换残差

步骤(4)中使用了柯西鲁棒核函数，列文伯格-马夸尔特算法，进行非线性优化。

柯西鲁棒核函数为：

其中，s为误差函数，c为控制参数，设置为1.5，使用该函数更新线性化可得：

其中，j为为的雅可比矩阵，为待优化的机器人状态量，使用步骤(2)中得到的机器人位姿预估值为初值，

使用列文伯格-马夸尔特算法修正方程式为：

其中h＝j^tj，b＝j^tf，通过启发式地调整λ来改善算法在局部极值附近的特性。

对解该方程，即可得到优化后的机器人位姿。

采用上述技术方案带来的有益效果：

本发明采用了使用了imu对uwb数据进行检验，采用柯西鲁棒核函数进行优化，显著的改善了uwb受到nlos影响导致定位数据不准确的情况

本发明使用了列文伯格-马夸尔特算法优化机器人位姿，进一步提升了系统定位精度。

本发明不仅能够显著的提高uwb/imu融合定位的定位精度，而且适用于其他的多机系统，具有广泛的应用前景。

附图说明

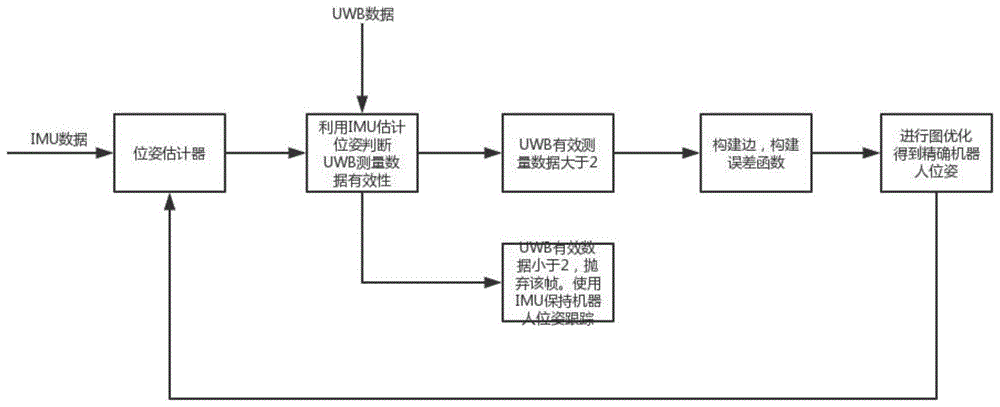
图1是本发明算法流程框图；

图2是本发明的uwb/imu，机器人布局图；

图3是机器人在场景中运动的位姿图；

具体实施方式

以下将结合附图，对本发明的技术方案进行详细说明。

本发明设计了一种基于图优化的uwb/imu的室内移动机器人协同定位方法，如图1所示，基本步骤如下：

(1)建立传感器观测模型

(2)初步校验uwb数据，判断数据是否受到nlos影响。

(3)构建机器人位姿优化图，构建误差函数，将机器人位置优化问题转化为位姿图优化问题。

(4)使用柯西鲁棒核函数，列文伯格-马夸尔特算法，优化机器人当前时刻的位姿。

在本实施例中，采用如下优选方案实现步骤1：

在(1)步骤中，所述uwb测量模型如下：

其中l1，l2，l3....ln为各基站到机器人的距离，(x1,y1,z`1),(x2,y2,z2),(x3,y3,z3).....(xn,yn,zn)表示为基站坐标，(xu,yu,zu)为机器人位置

按照权利要求1所述的一种基于图优化的uwb/imu的室内移动机器人定位方法其特征在于，在(1)步骤中，所述imu测量模型如下：

为机器人在j,i时刻的位置，为机器人j.i时刻在世界坐标系下的速度，g^w为世界坐标系下，机器人的重力加速度。δt为两次采样时间间隔。为imu预积分量。为imu加速度计，陀螺仪的整体偏移量，为整体偏移使用随机游走模型的参数变量。a,w为使用中值滤波法计算得到的机器人当前时刻线加速度与角速度。

在本实施例中，采用如下优选方案实现步骤2：

初步校验uwb数据，判断数据是否受到nlos影响。在k到k+1时刻有：

其中xk,xk-1为机器人在k，k-1时刻的位姿，因此可令

对rk进行检验，若则可认为uwb出现了异常测量值。

丢弃该测量值，记录uwb中有效测量的数量。

若此时有效数量m＜2，则该时刻的uwb帧无法作为定位使用，利用imu对该时刻进行保持。

若m＝2，由于室内环境中，地面相对平坦，可将z轴坐标看做一个常数，可令zk＝zk-1。

在本实施例中，采用如下优选方案实现步骤(3)，依照步骤2中的测量模型，构建误差函数

其中ei,eu,eui分别为imu测量残差，uwb测量残差，以及imu到uwb坐标转换残差在本实施例中，采用如下优选方案实现步骤(4)：使用了柯西鲁棒核函数，列文伯格-马夸尔特算法，进行非线性优化。

柯西鲁棒核函数为：

其中，s为误差函数，c为控制参数，设置为1.5，使用该函数更新线性化可得：

其中，j为为的雅可比矩阵，为待优化的机器人状态量，使用步骤(2)中得到的机器人位姿预估值为初值，

使用列文伯格-马夸尔特算法修正方程式为：

其中h＝j^tj，b＝j^tf，通过启发式地调整λ来改善算法在局部极值附近的特性。

对解该方程，即可得到优化后的机器人位姿。