基于IMF-PSD谱线的振动信号特征提取与刀具磨损值预测方法

本发明属于机械设备可靠性评估与健康管理，特别涉及一种基于eemd(集合经验模态分解)和功率谱密度的振动信号特征提取及刀具磨损量预测方法。

背景技术：

随着科技的发展与进步，机械设备在现代化工业应用中占据着重要地位，随着设备结构的愈加复杂，对机械设备运行过程信息进行特征提取及进一步诊断与评估也愈加重要。为了保证设备长期高效的正常运转，根据机电设备的健康状态，合理组织维修，可以避免过剩维修和维修不足。实施“预知维修”可以有效减少设备的维修费用，提高设备使用寿命，缩短不必要的停机时间。因此，对机械设备当前状态进行监测、诊断具有至关重要意义。

然而，当故障将要发生时，机械系统固有振荡的复杂性将发生变化，这给故障信号的分析处理带来了极大的困扰。为了检测机械设备故障，己经开发了许多种方法。目前，绝大多数的特征提取技术仅依靠传统的均方根、峰值进行特征提取，这种传统特征提取通常通过固定的算法提取出一系列数值，不考虑设备实际的运行环境和运行状态。此外仅仅得出数值变化不足以了解设备产生何种变化。

状态评估是机械设备可靠性评价及健康管理的不可或缺的关键环节之一，基于传统的寿命试验或加速寿命试验需要观测到设备的失效，试验样本量大、周期长、能耗高，此外，当前的监测技术还缺少对设备载荷跟设备状态联系，缺少对设备自身状态信息的监测收集与监测。

技术实现要素：

为了解决上述问题，本发明的实施方式立足于设备运行过程状态数据，根据集合经验模态分解(eemd)与功率谱密度分析的定义，提供了一种基于imf-psd谱的振动信号特征提取及刀具磨损量预测方法。本发明通过集合经验模态分解(eemd)对采集到的设备运行过程信号进行分解，利用功率谱密度(psd)对分解出来的固有模态函数(imf)进行功率谱密度的计算，随后根据相关性分析的方法，自适应地提取出相关性较高的imf-psd分量谱线，随后采用线性回归的方法拟合性能退化量预测刀具磨损值，为后续的状态评估等提供相应的技术依据。

根据本发明的实施方式提供了一种基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法，包括以下步骤：步骤一：采集原始信号，并利用集合经验模态分解对所述原始信号进行固有模态分解，在加入白噪声降噪的同时将原始信号依据幅值频率高到低依次展开，分解得到多个imf分量；步骤二：通过功率谱密度分析，得到步骤一中分解所得的每一个imf分量的psd谱线，并取平均值，获得imf-psd谱线；步骤三：对步骤二中获得的imf-psd谱线进行皮尔逊相关性分析，提取与退化量最相关的imf-psd分量谱线；步骤四：对步骤三中提取出的imf-psd分量谱线利用回归分析的方法建立预测模型；以及步骤五：通过步骤四中建立的回归模型预测刀具磨损值。

根据另一个可选的实施方式，所述步骤一还包括：

a)设定分解的迭代总次数为ne，初始化所加白噪声幅值；

b)在第m次分解添加白噪声的原始信号，m＝1,2…,ne，初始时令m＝1，为原始信号x(t)加上白噪声

xm(t)＝x(t)+nm(t)

其中，xm(t)代表第m次加噪后的信号，nm(t)代表第m次分解所添加的白噪声；

c)使用集合经验模态方法分解第m次加噪后的信号xm(t)，得到第m个imf分量imfm，m＝1,2,…,ne，如果m＜ne，则返回到步骤b)，并且m＝m+1，重复步骤b)和c)；

计算ne次分解后得到的ne个imf分量和信号残余量r(t)

根据另一个可选的实施方式，所述步骤二还包括：

令u(t)是一空间域内的函数，当u(t)是满足如下三个狄里克莱条件则可以作傅里叶变换，分别是具有有限个间断点、具有有限个极值点、绝对可积；若u(t)不满足狄利克雷条件，则不可以作傅里叶变换，但是若具有有限的平均功率，即满足公式则能够对函数进行截断：

其中，u(t)是空间域内的函数，为经过步骤一分解之后的imfm函数；

对函数进行傅里叶变换，为ut(v)

其中，t为时间，e为自然常数为数学中一个常数，是一个无限不循环小数，且为超越数，其值约为2.718281828459045，i为虚数单位，v为u(t)在频域内的角速度；

根据帕塞瓦尔定理，|ut(v)|²是截断信号ut(t)在频域内的能量分布，则ut(t)的归一化能谱密度为：

其中，t为信号u(t)的总频段；

上述表达式具有单位频段上功率的量纲，定义u(t)的功率谱密度为

通过功率谱密度分析即得到多状态信号在不同频率下能量的分布情况，即任务载荷在不同频率下的分布情况；

对其取平均值得到功率谱密度平均值：

其中k为psd谱线的频率点数；

对imf-psd谱的定义如下：设备运行过程中共采集了n组振动信号，对第p组振动信号xp(t)进行集合经验模态分解，得到ne个imf分量,对第p组振动信号中的imfm求功率谱密度平均值得到imfm-psdp,m＝1,2,...,ne；p＝1,2,3,...,n；共有ne条imf-psd曲线，则第p组振动信号的第m个imfm-psdp表示为：

在第m个imf分量下，由振动信号x1(t),x2(t),…,xne(t)所构成的imf-psd谱线表示如下：

imf-psdm＝[imf-psd1m,imf-psd2m,imf-psd3m,...,imf-psdnm]。

根据另一个可选的实施方式，所述步骤三还包括：

通过步骤二中采集的n组振动信号，计算得到ne条imf-psd谱线，将分解得到的ne条imf-psd谱线与实际性能退化曲线进行皮尔逊相关性分析，提取出h条相关系数大于0.8的imf-psd分量谱线；

给定二元总体(x，y)

其中，e(xy)、e(x)、e(y)代表期望，cov表示协方差，σx、σy代表方差。

根据另一个可选的实施方式，所述步骤四还包括：

对提取到的h条imf-psd谱线与性能退化曲线进行线性回归分析；

给定的x＝(x1；x2；x3；….xh)其中xh是第h条imf功率谱密度曲线，线性回归模型是一个多种函数通过线性组合来预测的函数，其中w为变量前的系数，b为函数截距

f(x)＝w1x1+w2x2+w3x3+…+whxh+b；

上述函数用向量的形式表示为

f(x)＝w^tx+b

其中，w＝(w1；w2；w3；…；wh)，w与b确定之后，就建立该复合模型的回归模型。

根据另一个可选的实施方式，步骤五还包括：根据建立的f(x)回归模型输入对应的x值，预测刀具磨损值。

根据另一个可选的实施方式，步骤一中采集原始信号包括从所述加工设备，或者与所述加工设备同类型、同工作环境的设备，采集从使用开始到完全故障的任意一段历史信号。

根据本发明的另一个实施方式提供了基于imf-psd谱的设备信号特征提取及刀具磨损值预测方法，包括如下步骤：

步骤1：利用eemd对采集的原始信号进行固有模态分解，在加入白噪声降噪的同时将原始信号从高频到低频依次展开，分解得到多个imf分量；

步骤2：计算步骤1中分解得到的每一个imf分量的功率谱密度值，并计算其imf-psd谱线；

步骤3：根据步骤2中计算的imf-psd谱线与性能退化量曲线做相关性分析，提取相关性大于0.8的功率谱密度曲线；

步骤4：对步骤3中提取的h个imf-psd谱线建立线性回归模型；

步骤5：将步骤4建立的线性回归模型用于预测性能退化量。

根据另一个可选的实施方式，步骤1中，所述原始信号包括当前设备，或者与当前设备同类型、同工作环境的设备，从使用开始到完全故障的任意一段历史信号。

根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法至少包括以下优点：1)充分利用集合经验模态分解整体性的特点将信号分解到不同的频带上，对不同频段的信号计算其功率谱密度，并且结合了集合经验模态将信号从高到低分解的特点和功率谱密度能不同任务信息的特点，从而在不同的工作条件下的所有信号，都能够自适应性的选择出固有模态函数(imf)的最佳数量；2)提出了imf-psd谱线的特征量，判断具体频带段的变化，本发明还可以对信号进行特征提取及寿命预测，这对于机械设备可靠性评价与健康监控的信号处理、特征提取等技术领域内高效、有效的进行自适应特征提取具有十分重要的意义。

附图说明

通过阅读下文优选实施方式的详细描述，各种其他的优点和益处对于本领域普通技术人员将变得清楚明了。附图仅用于示出优选实施方式的目的，而并不认为是对本发明的限制。而且在整个附图中，用相同的参考符号表示相同的部件。通过参考附图可更好地理解本发明。

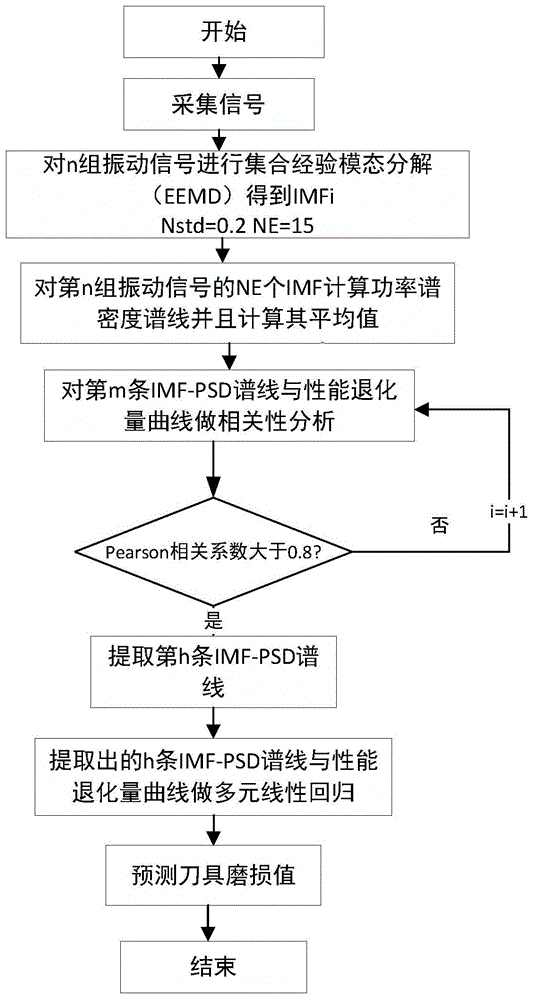
图1示出了根据本发明的实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图；

图2示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的传感器采集信号与性能退化量示意图；

图3示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中第一组振动信号经过功率谱密度计算的imf5-10；

图4示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中经过特征提取的imf-psd1-5特征与刀具磨损值对比；

图5示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中提取出的imf-psd1-5谱线三维图；

图6示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中拟合的回归曲线的散点图与回归线；

图7示出了应用本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中对刀具磨损值寿命预测结果。

图8示出了根据本发明的另一个实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图。

具体实施方式

下面将参照附图更详细地描述本公开的示例性实施方式。虽然附图中显示了本公开的示例性实施方式，然而应当理解，可以以各种形式实现本公开而不应被这里阐述的实施方式所限制。相反，提供这些实施方式是为了能够更透彻地理解本公开，并且能够将本公开的范围完整的传达给本领域的技术人员。

需要注意的是，除非另有说明，本发明使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。

下面将参照附图更详细地描述本发明的示例性实施方式。虽然附图中显示了本公开的示例性实施方式，然而应当理解，可以以各种形式实现本发明，而不应被这里阐述的实施方式所限制。相反，提供本实施方式是为了能够更透彻地理解本发明，并且能够将本公开的范围完整的传达给本领域技术人员。

需要注意的是，除非另有说明，本发明使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。

图1示出了根据本发明的实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图。参考图1，根据本发明的实施方式提供了一种基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法，包括以下步骤：步骤一：采集原始信号，并利用集合经验模态分解对所述原始信号进行固有模态分解，在加入白噪声降噪的同时将原始信号依据幅值频率高到低依次展开，分解得到多个imf分量；步骤二：通过功率谱密度分析，得到步骤一中分解所得的每一个imf分量的psd谱线，并取平均值，获得imf-psd谱线；步骤三：对步骤二中获得的imf-psd谱线进行皮尔逊相关性分析，提取与退化量最相关的imf-psd分量谱线；步骤四：对步骤三中提取出的imf-psd分量谱线利用回归分析的方法建立预测模型；以及步骤五：通过步骤四中建立的回归模型预测刀具磨损值。

根据另一个可选的实施方式，所述步骤一还包括：

a)设定分解的迭代总次数为ne，初始化所加白噪声幅值；

b)在第m次分解添加白噪声的原始信号，m＝1,2…,ne，初始时令m＝1，为原始信号x(t)加上白噪声

xm(t)＝x(t)+nm(t)

其中，xm(t)代表第m次加噪后的信号，nm(t)代表第m次分解所添加的白噪声；

c)使用集合经验模态方法分解第m次加噪后的信号xm(t)，得到第m个imf分量imfm，m＝1,2,…,ne，如果m＜ne，则返回到步骤b)，并且m＝m+1，重复步骤b)和c)；

计算ne次分解后得到的ne个imf分量和信号残余量r(t)

根据另一个可选的实施方式，所述步骤二还包括：

令u(t)是一空间域内的函数，当u(t)是满足如下三个狄里克莱条件则可以作傅里叶变换，分别是具有有限个间断点、具有有限个极值点、绝对可积；若u(t)不满足狄利克雷条件，则不可以作傅里叶变换，但是若具有有限的平均功率，即满足公式则能够对函数进行截断：

其中，u(t)是空间域内的函数，为经过步骤一分解之后的imfm函数；

对函数进行傅里叶变换，为ut(v)

其中，t为时间，e为自然常数为数学中一个常数，是一个无限不循环小数，且为超越数，其值约为2.718281828459045，i为虚数单位，v为u(t)在频域内的角速度；

根据帕塞瓦尔定理，|ut(v)|²是截断信号ut(t)在频域内的能量分布，则ut(t)的归一化能谱密度为：

其中，t为信号u(t)的总频段；

上述表达式具有单位频段上功率的量纲，定义u(t)的功率谱密度为

通过功率谱密度分析即得到多状态信号在不同频率下能量的分布情况，即任务载荷在不同频率下的分布情况；

对其取平均值得到功率谱密度平均值：

其中k为psd谱线的频率点数；

对imf-psd谱的定义如下：设备运行过程中共采集了n组振动信号，对第p组振动信号xp(t)进行集合经验模态分解，得到ne个imf分量,对第p组振动信号中的imfm求功率谱密度平均值得到imfm-psdp,m＝1,2,...,ne；p＝1,2,3,...,n；共有ne条imf-psd曲线，则第p组振动信号的第m个imfm-psdp表示为：

在第m个imf分量下，由振动信号x1(t),x2(t),…,xne(t)所构成的imf-psd谱线表示如下：

imf-psdm＝[imf-psd1m,imf-psd2m,imf-psd3m,...,imf-psdnm]。

根据另一个可选的实施方式，所述步骤三还包括：

通过步骤二中采集的n组振动信号，计算得到ne条imf-psd谱线，将分解得到的ne条imf-psd谱线与实际性能退化曲线进行皮尔逊相关性分析，提取出h条相关系数大于0.8的imf-psd分量谱线；

给定二元总体(x，y)

其中，e(xy)、e(x)、e(y)代表期望，cov表示协方差，σx、σy代表方差。

根据另一个可选的实施方式，所述步骤四还包括：

对提取到的h条imf-psd谱线与性能退化曲线进行线性回归分析；

给定的x＝(x1；x2；x3；....xh)其中xh是第h条imf功率谱密度曲线，线性回归模型是一个多种函数通过线性组合来预测的函数，其中w为变量前的系数，b为函数截距

f(x)＝w1x1+w2x2+w3x3+…+whxh+b；

上述函数用向量的形式表示为

f(x)＝w^tx+b

其中，w＝(w1；w2；w3；…；wh)，w与b确定之后，就建立该复合模型的回归模型。

根据另一个可选的实施方式，步骤五还包括：根据建立的f(x)回归模型输入对应的x值，预测刀具磨损值。

根据另一个可选的实施方式，步骤一中采集原始信号包括从所述加工设备，或者与所述加工设备同类型、同工作环境的设备，采集从使用开始到完全故障的任意一段历史信号。

图1示出了根据本发明的实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图。图2示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的传感器采集信号与性能退化量示意图。图3示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中第一组振动信号经过功率谱密度计算的imf5-10。图4示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中经过特征提取的imf-psd1-5特征与刀具磨损值对比。图5示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中提取出的imf-psd1-5谱线三维图。图6示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中拟合的回归曲线的散点图与回归线。图7示出了应用本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中对刀具磨损值寿命预测结果。图8示出了根据本发明的另一个实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图。

以下，参考附图对应用根据本发明的实施方式的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例进行详细说明。在该示例性实施例中，为更好地保证试验结果的准确度，本实施方式采用设备运行历史信号(下文简称原始信号)的信号作为试验依据进行分析，其中设备运行过程信号主要是指当前设备、或者与当前设备同类型、同工作环境的设备中，采集的从使用开始到完全故障的任意一段历史信号。本示例性实施例中所采用的待分解数据在2010年的phm协会的大数据比赛中对外公开。在铣削期间定期检测每把刀具的磨损量、力信号、声发射(ae)信号和振动信号。本示例性实施例中使用techrfm760高速铣床，刀具为硬质合金三刃球头铣刀，主轴旋转速度、进给速度等加工参数不变，刀具具体型号和加工条件如下所示：

在本切削条件下一共进行了六次全寿命周期试验，测得六组刀具磨损的振动信号，每组均切削315次，测得315个磨损值，其中磨损值及为本发明所述的性能退化量。图2示出了示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的第一组振动信号与刀具全寿命周期磨损值。

图1示出了根据本发明的实施方式提供的基于imf-psd的振动信号特征提取及刀具磨损值预测方法的流程图，具体包括如下步骤：

步骤1：利用eemd对原始信号进行固有模态分解

选取仿真叠加信号进行研究，其中加入白噪声信噪比nstd取0.2，迭代总次数ne选取15次，对输入的原始信号x(t)进行eemd，将原始信号由高频到低频展开。具体过程如下：

1)首先初始化所加白噪声幅值，第m次分解添加了白噪声的待分解信号，初始时令m＝1，

为原始信号x(t)加上白噪声

xm(t)＝x(t)+nm(t)

其中，nm(t)代表第m次分解所添加的白噪声，xm(t)代表第m次加噪后的信号。

2)使用经验模态方法分解加噪后的信号，得到15个imf分量；

如果m＜15，那么返回到步骤1)，并且m＝m+1；重复步骤1)和2)，

计算m次分解后每一个imf分量，以将原始信号分解成15个imf分量与信号残余分量：

其中，imfm为第m次分解得到的第m个imf分量；r(t)为信号残余分量。利用eemd对刀具切削振动信号进行分解，共获得315组分解信号其中包含imf1-15。图4展示了前五组振动信号imf1-5的时域图，

步骤2：利用功率密度分析的方法计算每一个imfm分量的功率谱能量，并计算其平均值，获得imf-psd谱线具体过程如下：

本实施选择计算功率谱密度中，采样频率fs设置为50000。

计算315组振动信号imf1-10的功率谱密度，其中每组的imfm表示为u(t)。

其中，i为虚数单位，v为u(t)在频域内的角速度,u(t)为每组的imf。

|ut(v)|²是原始信号ut(t)在频域内的能量分布，则ut(t)的归一化能谱密度为：

其中，t为信号u(t)的总频段。

此表达式具有单位频段上功率的量纲，因此，从逻辑上可以定义u(t)的功率谱密度为

通过功率谱密度分析即可得到多状态信号在不同频率下能量的分布情况。

并取平均值：

其中k是psd(v)的功率谱点数。

表1示出了对应用根据本发明的实施方式的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法的示例性实施例中，计算第一组的每个imf1-10的功率谱密度平均值。

表1第一组振动信号imf1-10的功率谱密度平均值

(a)

(b)

上表中，表示分解第一组振动信号的第m个imf分量的平均功率谱密度；依次类推，表示分解第一组的振动信号的第9个imf分量的功率谱密度平均值。共有315组数据，累积共有315*10组功率谱密度值。

在本发明中对n组振动信号un(t)进行eemd分解，则得到ne个imf，第i个imf的功率谱密度psd表示为：

式中：表示振动信号x(t)分解后的第i个imf的功率谱密度。则本发明对imf-psd谱的定义如下：假设设备运行过程中共采集了n组振动信号，对第p组振动信号xp(t)进行eemd分解，得到ne个imf分量，对第p组振动信号中的imfm求功率谱密度平均值得到imfm-psdp,m＝1,2,...,ne；p＝1,2,3,...,n；共有ne条imf-psd曲线，则第p组振动信号的第m个imfm-psdp表示为：

在第m个imf分量下，由振动信号x1(t),x2(t),…,xne(t)所构成的imf-psd谱线表示如下：

imf-psdm＝[imf-psd1m,imf-psd2m,imf-psd3m,...,imf-psdnm]。

步骤3：根据步骤2中获得的imf-psd谱线，利用相关性分析的方法提取含有复杂信息最多的imf分量。

计算得到ne条imf-psd谱线，将分解得到的ne条imf-psd谱线与实际性能退化曲线做皮尔逊相关分析，提取出h条关系数大于0.8的imf-psd分量谱线。

给定二元总体(x，y):

其中，e(xy)、e(x)、e(y)代表期望，cov表示协方差,σx、σy代表方差。

表2示出了计算所有振动信号的每个imf1-10的功率谱密度平均值。

(a)

(b)

由上表2可得知，imf-psd1-5谱线与性能退化曲线的pearson(皮尔逊)相关系数大于0.8，与性能退化量有着高度相关性。因此提取功率谱密度平均值imf-psd1-5作为关键拟合参数。图3示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的第一组振动信号的imf1-5的功率谱密度谱线。

步骤4：提取出的5条imf-psd谱线，与性能退化值做线性回归模型。

给定的x＝(x1；x2；x3；x4；x5),线性回归模型是一个多种函数通过线性组合来预测的函数

f(x)＝w1x1+w2x2+w3x3+…+whxh+b

一般用向量的形式写成：

f(x)＝w^tx+b

其中，w＝(w1；w2；w3；…；wh),xh是第h条imf功率谱密度曲线，w为变量前的系数，b为函数截距。w与b确定之后，就可以确定该复合模型的回归模型。

图4示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的被提取的imf-psd1-5与刀具磨损值的对比图。

图5示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的imf-psd1-5的imf组数、振动组数、功率谱密度值的三维图。

根据线性回归模型得出：

y＝129.1246+2.8179x1+1.2333x2-0.4697x3-0.0314x4-0.0505x5。

图6示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的预测回归曲线的散点图与回归线。从图中可以看出散点图均匀的分布在回归线附近，表明该线性回归拟合精度较高。

步骤5：将步骤4建立的线性回归模型用于预测性能退化量。

表3预测刀具磨损值与实际刀具磨损值之间的相对误差。

图7示出了应用根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法示例性实施例中的刀具磨损量预测值与实际值对比图。

根据表3所示结果，可以知道本发明的实施方式所提供的方法可以有效的解决已知刀具切削时振动信号下刀具磨损值预测问题，从表3中可以看出，使用本发明的实施方式所提出的刀具磨损值预测方法，其理论值与计算值实际误差小，具有较高的精度，验证了所述方法的有效性。

综上，通过以上步骤，根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法能够自适应的得到不同情况下的振动信号的特征频带段，不仅可以自适应的从过程信号中提取最佳的固有模态函数个数，同时也可以对运行过程的性能退化量进行预测，对于高效、有效的进行自适应特征提取与寿命预测具有十分重要的意义。

特别地，根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法可以根据不同状况下的信号自适应的提取最佳固有模态函数数量，对不同情况下的固有模态函数的选择提供一定的参考指导。根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法不仅适用于案例中所设置的phm2010公开数据，还可以适用于其他机械设备及其关键零部件中，为特征提取提供合理的参考。此外，根据本发明的实施方式所提供的基于imf-psd谱线的振动信号特征提取与刀具磨损值预测方法具有良好的拓展能力，为本技术领域的其他技术人员提供一定的借鉴作用。

需要说明的是，本发明的说明书附图中的流程图和框图显示了根据本发明的多个实施例的系统、方法的可能实现的体系架构、功能和操作。在这点上，流程图或框图中的每个方框可以代表一个模块、程序段或代码的一部分，所述模块、程序段或代码的一部分包含一个或多个用于实现规定的逻辑功能的可执行指令。也应当注意，在有些作为替换的实现中，方框中所标注的功能也可以以不同于附图中所标注的顺序发生。例如，两个连续的方框实际上可以基本并行地执行，它们有时也可以按相反的顺序执行，这依所涉及的功能而定。也要注意的是，框图和/或流程图中的每个方框、以及框图和/或流程图中的方框的组合，可以用执行规定的功能或动作的专用的基于硬件的系统来实现，或者可以用专用硬件与计算机指令的组合来实现。

以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的保护范围当中。

在本发明所提供的几个实施例中，应该理解到，所披露的装置和方法，可以通过其它的方式实现。以上所描述的装置实施例仅仅是示意性的，例如，所述单元的划分，仅仅为一种逻辑功能划分，实际实现时可以有另外的划分方式，又例如，多个单元或组件可以结合或者可以集成到另一个系统，或一些特征可以忽略，或不执行。

所述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物理单元，即可以位于一个地方，或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部单元来实现本实施例方案的目的。

另外，在本发明各个实施例中的各功能单元可以集成在一个处理单元中，也可以是各个单元单独物理存在，也可以两个或两个以上单元集成在一个单元中。

此外，前述仅说明了一些实施方式，可进行改变、修改、增加和/或变化而不偏离所公开的实施方式的范围和实质，该实施方式是示意性的而不是限制性的。此外，所说明的实施方式涉及当前考虑为最实用和最优选的实施方式，其应理解为实施方式不应限于所公开的实施方式，相反地，旨在覆盖包括在该实施方式的实质和范围内的不同的修改和等同设置。此外，上述说明的多种实施方式可与其它实施方式共同应用，如，一个实施方式的方面可与另一个实施方式的方面结合而实现再另一个实施方式。另外，任何给定组件的各独立特征或构件可构成另外的实施方式。

以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。