一种前向放大系数不一致时的半球谐振陀螺振型角获取方法

本发明涉及前向放大系数不一致时的半球谐振陀螺振型角获取方法，属于惯性技术领域。

背景技术：

上世纪60年代，出现了一种新型振动陀螺，半球谐振陀螺。此新型陀螺具备许多优点，例如误差小、工作寿命长、应用领域广等优点。不仅如此，相比于传统机械陀螺，半球谐振陀螺组成部件少，结构简单，其表头仅由二到三件零部件组成，且不易磨损，故障率非常低。半球谐振陀螺的核心部件谐振子是由熔融石英制成的，由于石英玻璃稳定的物理特性，因此谐振子不仅可靠性高、工作寿命长，而且具有极强的抗辐射能力，不易受宇宙射线及高能粒子的干扰，常用于空间飞行器的定姿与导航。综上所述，半球谐振陀螺具有极好的发展前景，对半球谐振陀螺进行研究，有益于惯性技术的发展与创新，可以为我国的深空探测以及其它相关的高科技领域进一步打下良好的基础。

现阶段，半球谐振陀螺主要有力平衡和全角两种工作模式，全角模式是一种新型半球谐振陀螺工作模式，该模式是利用谐振子进动角度与陀螺载体转动角度呈正比这一物理特性，通过对谐振子振型的进动角度的实时解算来读出载体的转动角度，适合于转速较高的场合。全角模式下，通常会对0°和45°电极采集到的信号x、y进行等比例的前向放大，再计算振型的进动角度，但这存在一个值得考虑问题：如果两个信号的放大系数不相等时，那么常用的测角方程就不够精确，计算出来的振型角会与实际的振型角存在不小的误差，解算后读出的载体转动角度与载体实际转角也会存在一定误差，这在高精度应用场合中是不允许存在的情况。

综上所述，想要计算出精确的振型角，就必须知道前向放大系数比值k的精确大小。因此，提出一种高精度的辨识方法来辨识出k，是十分必要的。

技术实现要素：

本发明的目的是为了解决前向放大系数不一致时半球谐振陀螺无法精确测出载体的角度等信息，降低导航准确率的问题，而提出一种前向放大系数不一致时的半球谐振陀螺振型角获取方法。

载体可以是飞行器、转台等等。

一种前向放大系数不一致时的半球谐振陀螺振型角获取方法具体过程为：

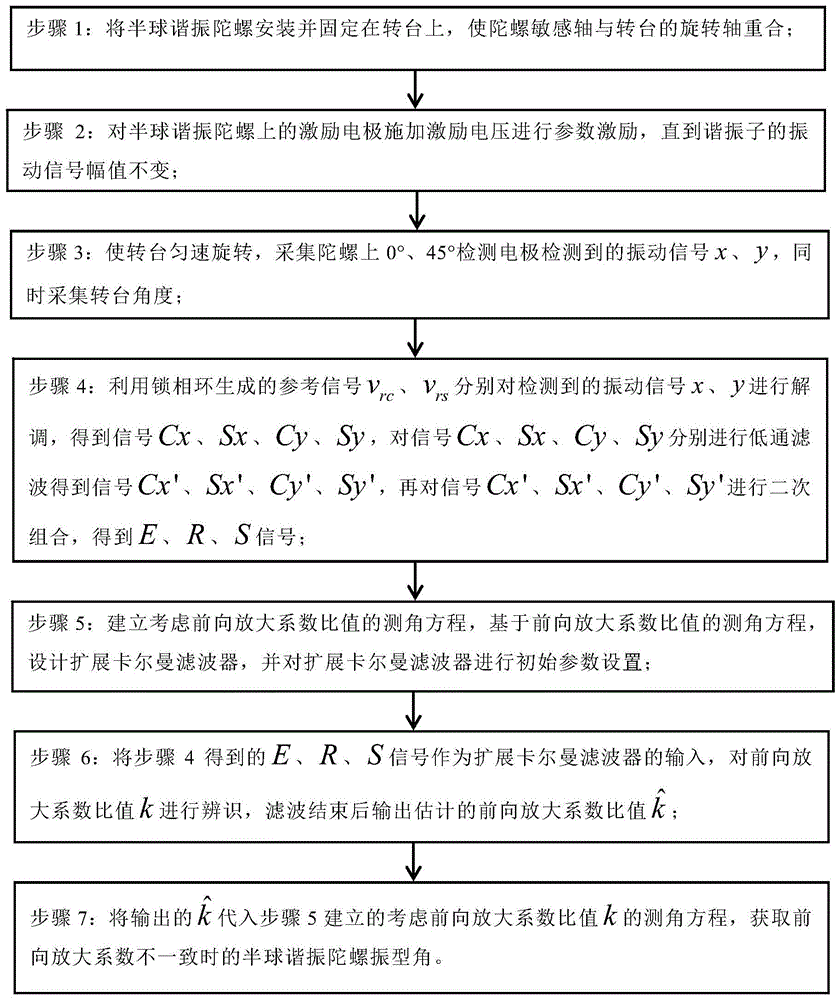
步骤1：将半球谐振陀螺安装并固定在转台上，使陀螺敏感轴与转台的旋转轴重合；

步骤2：对半球谐振陀螺上的激励电极施加激励电压进行参数激励，直到谐振子的振动信号幅值不变；

步骤3：使转台匀速旋转，采集陀螺上0°、45°检测电极检测到的振动信号x、y，同时采集转台角度θr；

步骤4：利用锁相环生成的参考信号vrc、vrs分别对检测到的振动信号x、y进行解调，得到信号cx、sx、cy、sy，对信号cx、sx、cy、sy分别进行低通滤波得到信号cx'、sx'、cy'、sy'，再对信号cx'、sx'、cy'、sy'进行二次组合，得到e、r、s信号；

步骤5：建立考虑前向放大系数比值k的测角方程，基于前向放大系数比值k的测角方程，设计扩展卡尔曼滤波器，并对扩展卡尔曼滤波器进行初始参数设置；

步骤6：将步骤4得到的e、r、s信号作为扩展卡尔曼滤波器的输入，对前向放大系数比值k进行辨识，滤波结束后输出估计的前向放大系数比值

步骤7：将输出的代入步骤5建立的考虑前向放大系数比值k的测角方程，获取前向放大系数不一致时的半球谐振陀螺振型角。

本发明的有益效果为：

传统的测角方程默认前向放大系数是等比例的情况，没有考虑前向放大系数不一致的问题，计算出来的载体的角度等信息就会存在一定误差，降低了陀螺的精度，降低了导航准确率，无法满足高精度的工作场合的需求。

本发明提出了一种前向放大系数不一致时的半球谐振陀螺振型角获取方法，首先将半球谐振陀螺固定安装在转台上，使陀螺敏感轴与转台的旋转轴重合，然后对间隔布置在半球谐振陀螺上的激励电极施加激励电压进行参数激励，直到谐振子的振动信号幅值稳定。使转台匀速旋转，采集陀螺上0°、45°检测电极检测到的振动信号x、y，并利用锁相环生成的参考信号vrc、vrs分别对x、y进行解调、低通滤波、二次组合后得到e、r、s信号。基于改进的测角方程，完成扩展卡尔曼滤波器的设计后将步骤4得到的信号e、r、s作为扩展卡尔曼滤波器的输入，对k进行辨识，滤波结束后输出最后将辨识的代入改进的测角方程中，得到精确的测角方程。该方法可以实现前向放大系数比值k的精确辨识，具有很高的精度，辨识的误差小，通过计算得到的陀螺振型角精度高，实现了陀螺的高精度角度测量，精确测出载体的角度信息，提高导航准确率；解决前向放大系数不一致时半球谐振陀螺无法精确测出载体的角度等信息，降低导航准确率的问题。

本发明通过理论分析和仿真实验可以看出，本发明提出的一种前向放大系数不一致时的半球谐振陀螺振型角获取方法能够实现全角模式半球谐振陀螺在前向放大系数不一致时的高精度工作，从而广泛应用到需要高精度半球谐振陀螺的高端科技领域中。

附图说明

图1为本发明流程图；

图2为本发明实施例参数k辨识误差曲线图；

图3为本发明实施例振型角误差曲线图；

图4为半球谐振陀螺上的激励电极布置图。

具体实施方式

具体实施方式一：结合图1说明本实施方式，本实施方式一种前向放大系数不一致时的半球谐振陀螺振型角获取方法具体过程为：

本发明的目的是针对于半球谐振陀螺检测回路前向放大系数不相等时测角存在误差的问题，提供一种前向放大系数不一致时的半球谐振陀螺振型角获取方法，提出改进的测角公式，基于此公式建立扩展卡尔曼滤波器，在转动陀螺的同时，对0°和45°电极采集到的振动信号进行解调、低通滤波等处理，得到的信号e、r、s作为扩展卡尔曼滤波器的输入，实现了前向放大系数比值k的辨识，得到精确的测角公式，提高陀螺的测量精度。

为了达到上述目的，本发明提供了一种前向放大系数不一致时的半球谐振陀螺振型角获取方法，包含：

步骤1：将半球谐振陀螺安装并固定在转台上，使陀螺敏感轴与转台的旋转轴重合；

步骤2：对半球谐振陀螺上的激励电极施加激励电压进行参数(激励电极施加的信号，如信号的幅值、频率、相位)激励，直到谐振子的振动信号幅值不变；

步骤3：使转台匀速旋转，采集陀螺上0°、45°检测电极检测到的振动信号x、y，同时采集转台角度θr；

步骤4：利用锁相环生成的参考信号vrc、vrs分别对检测到的振动信号x、y进行解调，得到信号cx、sx、cy、sy，对信号cx、sx、cy、sy分别进行低通滤波得到信号cx'、sx'、cy'、sy'，再对信号cx'、sx'、cy'、sy'进行二次组合，得到e、r、s信号；

步骤5：建立考虑前向放大系数比值k的测角方程，基于前向放大系数比值k的测角方程，设计扩展卡尔曼滤波器，并对扩展卡尔曼滤波器进行初始参数设置；

步骤6：将步骤4得到的e、r、s信号作为扩展卡尔曼滤波器的输入，对前向放大系数比值k进行辨识，滤波结束后输出估计的前向放大系数比值

步骤7：将输出的代入步骤5建立的考虑前向放大系数比值k的测角方程，获取前向放大系数不一致时的半球谐振陀螺振型角。

具体实施方式二：本实施方式与具体实施方式一不同的是，所述步骤2中激励电极间隔布置在半球谐振陀螺上。如图4所示。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是，所述步骤4中利用锁相环生成的参考信号vrc、vrs分别对检测到的振动信号x、y进行解调，得到信号cx、sx、cy、sy，对信号cx、sx、cy、sy分别进行低通滤波得到信号cx'、sx'、cy'、sy'，再对信号cx'、sx'、cy'、sy'进行二次组合，得到e、r、s信号；具体过程为：

所述利用锁相环生成的参考信号vrc、vrs分别对检测到的振动信号x、y进行解调，得到信号cx、sx、cy、sy，表达式为：

将信号cx、sx、cy、sy经过低通滤波，分别滤除信号cx、sx、cy、sy中的二倍频，得到信号cx'、sx'、cy'、sy'；

对信号cx'、sx'、cy'、sy'进行二次组合，得到e、r、s信号。

其它步骤及参数与具体实施方式一或二相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是，所述对信号cx'、sx'、cy'、sy'进行二次组合，得到e、r、s信号，表达式为：

其它步骤及参数与具体实施方式一至三之一相同。

具体实施方式五：本实施方式与具体实施方式一至四之一不同的是，所述参考信号vrc、vrs由正弦信号和余弦信号组成。

其它步骤及参数与具体实施方式一至四之一相同。

具体实施方式六：本实施方式与具体实施方式一至五之一不同的是，所述步骤5中建立考虑前向放大系数比值k的测角方程；具体过程为：

建立考虑前向放大系数比值k的测角方程，该公式能精确描述振型的真实进动角，形式如下：

其中，k＝ky/kx，kx为0°电极的前向放大系数，ky为45°电极(确定了0°电极后，逆时针方向45°就是45°电极)的前向放大系数；θreal为半球谐振陀螺振型角真实值。

因此，只要知道参数k，就能直接求得半球谐振陀螺振型角真实值θreal。

其它步骤及参数与具体实施方式一至五之一相同。

具体实施方式七：本实施方式与具体实施方式一至六之一不同的是，所述步骤5中基于前向放大系数比值k的测角方程，设计扩展卡尔曼滤波器，滤波器选取的模型如下所示：

k(i+1)＝k(i)、c(i+1)＝c(i)是状态方程，为陀螺前向放大系数比值k＝ky/kx以及陀螺进动系数c，这两个参数为不随时间改变的固定值k(i)为前向放大系数比值，c(i)为陀螺进动系数，i为第i个时刻；

是观测方程，θr为转台转角，v为测量噪声；

所述步骤5中对扩展卡尔曼滤波器进行初始参数设置；具体过程为：

扩展卡尔曼滤波是一种递推算法，扩展卡尔曼滤波器启动时进行初始参数设置，给定初始值，令p0|0＝i；

式中，为前向放大系数比值k的初始估计值，为进动系数c的初始估计值，p0|0为估计误差协方差矩阵的初始值。

其它步骤及参数与具体实施方式一至六之一相同。

具体实施方式八：本实施方式与具体实施方式一至七之一不同的是，所述步骤6中将步骤4得到的e、r、s信号作为扩展卡尔曼滤波器的输入，对前向放大系数比值k进行辨识，滤波结束后输出估计的前向放大系数比值辨识具体步骤如下：

s1：对下一时刻的状态估计值进行预测

式中，为前向放大系数比值k第i个时刻的先验估计值，为前向放大系数比值k第i-1时刻的估计值，为进动系数c第i个时刻的先验估计值，为进动系数c第i-1时刻的估计值；

s2：对下一时刻的估计误差协方差进行预测：

pi|i-1＝pi-1|i-1

式中，pi|i-1为估计误差协方差矩阵第i时刻的预测值，pi-1|i-1为估计误差协方差矩阵第i-1时刻的值；

s3：判断是否还有信号e、r和s输入扩展卡尔曼滤波器，若有则跳到s4，若无则跳到步骤s9；

s4：对下一时刻的测量矩阵进行预测：

令

式中，b为中间变量，ci为第i个时刻的测量矩阵；

s5：对下一时刻的测量估计值进行预测：

其中，为转台转角的估计值；

s6：对下一时刻的状态增益矩阵进行预测：

ki＝pi|i-1*ci^t*(ci*pi|i-1*ci^t+q)^-1

式中，q为噪声v的协方差，可取q＝0.01²；*为乘号，ki为第i个时刻的状态增益矩阵，t为转置；

s7：对下一时刻的状态估计值进行更新：

式中，为前向放大系数比值k第i个时刻的后验估计值；

s8：对下一时刻的估计误差协方差进行更新，然后跳转到s1；

pi|i＝(i-kici)*pi|i-1

式中，pi|i为估计误差协方差矩阵第i个时刻的值，i为单位矩阵；

s9：滤波结束，输出估计的前向放大系数比值

综上，完成了基于考虑前向放大系数比值k的测角方程的扩展卡尔曼滤波器的设计。

其它步骤及参数与具体实施方式一至七之一相同。

具体实施方式九：本实施方式与具体实施方式一至八之一不同的是，所述步骤7中将输出的代入步骤5建立的考虑前向放大系数比值k的测角方程，获取前向放大系数不一致时的半球谐振陀螺振型角；表达式为：

式中，θguji为半球谐振陀螺振型角的估计值。

所述其它步骤及参数与具体实施方式一至八之一相同。

具体实施方式十：本实施方式与具体实施方式一至九之一不同的是，所述前向放大系数不一致由前向放大电路误差、谐振子电极极板面积误差、谐振子电极极板间距误差、谐振子安装偏差中的一种或多种导致；

所述多种为2种、3种或4种。

其它步骤及参数与具体实施方式一至九之一相同。

采用以下实施例验证本发明的有益效果：

实施例一：

步骤1，将半球谐振陀螺安装并固定在转台上，使陀螺敏感轴与转台的旋转轴重合；

步骤2，对间隔布置在半球谐振陀螺上的激励电极施加激励电压进行参数激励，直到谐振子的振动信号幅值稳定；

步骤3，使转台以ωr＝30°/s的速度匀速旋转，设定采样频率为fs＝1000hz，采样时间为ti＝10s，采集陀螺上0°、45°检测电极检测到的振动信号x、y，同时采集转台角度θr，其中0°检测电极前向放大系数为kx＝2，45°检测电极前向放大系数为ky＝2.2，则k＝ky/kx＝1.1；

步骤4，利用锁相环生成的参考信号vrc、vrs分别对所述的振动信号x、y进行解调，得到信号cx、sx、cy、sy，低通滤波后得到cx'、sx'、cy'、sy'，再进行二次组合，得到e、r、s信号，所述的参考信号vrc、vrs由正弦信号和余弦信号组成；

步骤5，基于考虑前向放大系数比值k的测角方程，完成扩展卡尔曼滤波器的设计，滤波器模型如下：

并将滤波器初始参数设置为p0|0＝i，测量噪声协方差q＝0.01²。

步骤6，将步骤4得到的信号e、r、s作为扩展卡尔曼滤波器的输入，对k进行辨识，滤波结束后输出

s1：对下一时刻的状态估计值进行预测

s2：对下一时刻的估计误差协方差进行预测：

pi|i-1＝pi-1|i-1

s3：判断是否还有实验数据输入，若有则跳到s4，若无则跳到步骤s9；

s4：对下一时刻的测量矩阵进行预测：

令

s5：对下一时刻的测量估计值进行预测：

其中，为转台转角的估计值

s6：对下一时刻的状态增益矩阵进行预测：

ki＝pi|i-1*ci^t*(ci*pi|i-1*ci^t+q)^-1

s7：对下一时刻的状态估计值进行更新：

s8：对下一时刻的估计误差协方差进行更新，然后跳转到s1：

pi|i＝(i-kici)*pi|i-1*(i-kici)^t

s9：滤波结束，输出估计的前向放大系数比值

仿真结果如图2所示，从图2可以看出扩展卡尔曼滤波器在5秒时辨识误差已趋于平稳，在采样时间里滤波器一共输出了10000个值，取最后辨识的可以得到最终辨识的与实际k的差值约等于2×10^-5，可以看出滤波器对k辨识精度很高。

步骤7，将输出的代入步骤5建立的考虑前向放大系数比值k的测角方程，获取前向放大系数不一致时的半球谐振陀螺振型角；表达式为：

计算得到估计振型角θguji与真实振型角θreal之间的位置误差，绘制的位置误差曲线如图3；

由图3曲线可知，位置误差范围始终处在[-0.0012°,0.0012°]，该方法估计的振型角θguji具有很高的精度。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。