一种用于行波管高能量小半径电子注的检测方法

1.本发明属于行波管技术领域，涉及一种用于行波管高能量小半径电子注的检测方法。


背景技术：

2.行波管具有工作频带宽、输出功率大、效率高、动态范围大、环境适应性强等一系列优点，是目前使用最多的微波电真空器件，广泛用于各种通信系统。
3.但高效率是目前电真空器件设计的难点和重点，而高性能行波管的实现不光在设计上要不断提升，保证加工制造与设计的吻合也极其重要。特别是目前测试手段有限、中间过程难以把握。行波管中电子注从电子枪中发射出来之后，与高频电路产生互作用之后，由收集极进行电子注回收。电子枪作为行波管中发射电子的部件，其发射出来的电子注状态将会直接影响到后续的互作用，从而对整管的各种性能指标产生极大的影响。
4.传统方法对于电子枪的电子注发射能力采用法拉第杯进行检测，但随着行波管的频率越来越高，用于行波管的高能电子注正在往能量越来越高、半径越来越细的方向发展。在此情况下，法拉第杯的探头在高能电子注轰击之下寿命也越来越短，且轰击出来的二次电子对检测结果会产生影响。同时法拉第杯的尺寸已不再适用于检测半径较小的电子注。因此亟需新的检测方法及装置对高能量且小半径的电子注进行精准检测，以获取其注腰半径和注腰位置，为后续行波管的整体设计制造做准备。


技术实现要素：

5.针对上述存在的问题或不足，为了解决现有行波管高能量小半径电子注无法被准确检测的问题，本发明提供了一种用于行波管高能量小半径电子注的检测方法。通过对电子注进行预处理后，可以在保证能够推断出电子注注腰半径和注腰位置的前提下，以目前常规检测手段进行电子注的检测，从而实现高能量小半径电子注的检测。
6.一种用于行波管高能量小半径电子注的检测方法，包括以下步骤：
7.s1.对待测行波管电子枪进行仿真得到其注腰位置z
w
和注腰半径r
w
，再将电子透镜组和荧光屏依次加载至待测行波管电子枪的模型末端，进行整体建模；
8.所述电子透镜组由第一电极片m1和第二电极片m2组成，电极片的面积大于电子注在对应电极片位置时的横截面，两电极片均设有十字狭缝，且十字狭缝的交汇处为一个圆通孔；电极片上圆通孔的圆心和电子枪同轴，且电极片、荧光屏均与待测行波管电子枪的末端平行。
9.所述第一电极片m1靠近电子枪的末端，第二电极片m2靠近荧光屏；荧光屏用于获取电子注在其位置处的所有电子，且不影响其位置之前的电子注的状态即可。
10.第一电极片m1的电压为u1，厚度为h1，圆通孔的半径为r1，十字狭缝的缝宽为a1，圆通孔的圆心到十字狭缝顶端的长度为b1；第二电极片m2的电压为u2，厚度为h2，圆通孔的半径为r2，十字狭缝的缝宽为a2，圆通孔的圆心到十字狭缝顶端的长度为b2。m1前端至电子枪
末端距离为l1，m1末端至m2前端距离为l2，m2末端至荧光屏前端距离为l3，l4为m1末端与荧光屏前端之间的距离；m1末端的轴向坐标设为z4。
11.u1和电子枪末端的电压相等,u2为200
‑
500v，荧光屏和u2的电压相等。
12.z4＝z
w
，l2由m1和m2之间的压差决定，以每1000v压差距离为1mm计数，l2需满足如下要求：l2>|u1‑
u2|/1000；l3初始保持在2mm
‑
8mm；0.1mm＜h1＜0.5mm，h1/2≤h2≤2h1(优选h1＝h2)，r
w
/2>r1>r
w
/3,a1≤r1,b1≥3*r1，2*r
w
＜r2＜3*r
w
,a2≤r2,b2≥3*r2。
13.s2.通过对s1所建模型仿真分别获取荧光屏与m1处的电子注轴向截面电子分布图，并得到图中所有电子的坐标数据，计算出这两幅图的h，m1处为h1，荧光屏处为h2，h的具体计算方法如下：
14.电子枪发射的电子注经过两电极片后，其轴向截面电子分布图形状为小孔带十字狭缝(如图1所示)。根据轴向截面电子分布图中所有电子的坐标数据，采用散点轮廓算法(alpha shape)获取截面电子分布图的外部轮廓，如图2所示。统计轮廓上的点，求出各点到图中心的距离，取其平均值定为h。其中散点轮廓算法原理为业内公知，在此不再赘述。
15.s3.保持l1,l2,l3,l4不变，测出h1,h2，取n1＝h2/h1，n1为电子注轴向截面的放大倍数；改变l3，上述数据测出n组(n≥3即满足要求，组数越多精度越高)，则l3,l4,h1,h2,n1均为一行n列的向量。对n1,l4进行高斯拟合，得到对应的函数称为电子注截面有效增益函数，定义域终点大于m2轴向坐标即可。
16.在本步骤中，l3每次改变，电子注的z
w
和r
w
均会有微小变化，但模拟后发现变化量均小于0.001mm，故可认为该过程z
w
和r
w
此二者保持不变。则电子注截面有效增益函数可求出任意轴向位置处电子注半径和荧光屏处电子注半径之间的放大倍数。注腰位置z
w
为轴向电子注半径最小位置，因此电子注截面有效增益函数在电子注轴向上的第一个极大值点必在电子注的注腰位置附近。
17.s4.将l3、z4恢复至步骤s3之前，测量荧光屏处h的数据，设为h'2，将l4代入电子注截面有效增益函数，求出此时m1与荧光屏处电子注半径的放大倍数n2,根据h'2与n2计算出此时m1处的h数据，设为h1'。
18.z4前后移动6
‑
14mm范围内再取f个横截面，求出f个横截面相应的h数据，加上h1'构成一行f+1列的向量(f≥4即可，f越大精度越高)，并将f+1列的向量设为h3，将h3对应的轴坐标的向量设为z3，对其进行≥3阶的傅里叶拟合得到电子注包络函数。
19.此过程仅仅选择了z4附近的横截面参与计算，并未移动m1，消除了移动电极片时注腰位置和注腰半径的变化，可降低计算误差。求出该函数在电子注轴向上的极小值和极小值点，即电子注的注腰半径和注腰位置。
20.s5.对s4所得电子注的注腰半径和注腰位置增加修正常量，修正常量为注腰半径数值加上0.05～0.15mm，注腰位置减去2.95mm～3.05mm后，则修正后的数据即为最终的电子注的注腰半径和注腰位置。
21.因高斯拟合与傅里叶拟合过程本身包含较小的误差，同时在得到电子注截面有效增益公式时，实测注腰半径和注腰位置每次会有较小改变，因此存在系统误差。同时在后续傅里叶拟合求得电子注包络函数时误差被累积、放大，因此需增加修正常量。
22.进一步的，所述荧光屏和电极片均为无氧铜材料(无氧铜材料具有优良的散热性，可以提高电极片在电子轰击下的散热情况，钼材料也可，除此之外的其余材料也可，但效果
不佳)。
23.综上所述，本发明提供的检测方法，对现有电子注的检测提供了一种方法，通过将电子注进行降压扩散(即降低能量，降低电流密度)处理，在保证电子注能量分布曲线的情况下，使之能够对高能量小半径电子注开展检测工作，分析电子注状态，指导空间行波管电子枪的设计工作，保障整管性能。
附图说明
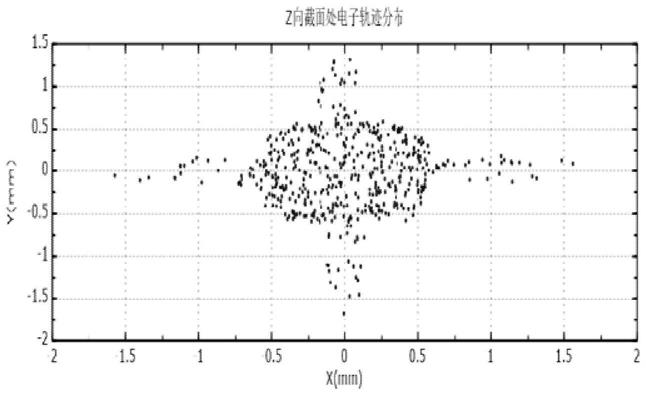
24.图1为实施例电子注在荧光屏处的电子轨迹分布图；
25.图2为实施例散点轮廓算法所绘制的电子注m1处电子轨迹分布图轮廓；
26.图3为实施例电子注截面有效增益曲线；
27.图4为实施例s1建立的模型图；
28.图5为实施例s4电子注包络拟合结果图；
29.图6为实施例电子注注腰半径收敛曲线；
30.图7为实施例电子注注腰位置收敛曲线；
31.图8为实施例电子轨迹在yz平面的投影。
具体实施方式
32.以某空间行波管的电子枪为例，对本发明的技术方案的具体实施方式做进一步的说明，其操作步骤如下：
33.s1.对待测行波管电子枪进行仿真得到其注腰位置z
w
和注腰半径r
w
，再将电子透镜组和荧光屏依次加载至待测行波管电子枪的模型末端，进行整体建模，如图4所示。
34.所述第一电极片m1靠近电子枪的末端，第二电极片m2靠近荧光屏；荧光屏用于获取电子注在其位置处的所有电子，并不影响其位置之前的电子注的状态即可。初始参数数据如下：
35.u1＝6000v,h1＝0.2mm,r1＝0.1mm,a1＝0.1mm,b1＝0.95mm；
36.u2＝200v,h2＝0.2mm,r2＝0.6mm,a2＝0.36mm,b2＝1.7mm；
37.l1＝2mm,l2＝6mm,l3＝3mm,l4＝9.2mm,z4＝11.12mm
38.m1和电子枪末端的电压相等，荧光屏和m2的电压相等。
39.电子枪发射的电子注经过两电极片后，其轴向截面电子分布图形状为小孔带十字狭缝(如图1所示)，主要尺寸为圆通孔半径r，图中狭缝高度到小孔中心的距离h，本发明主要采用数据h进行计算。
40.s2.通过对s1所建模型仿真分别获取荧光屏与m1处的电子注轴向截面电子分布图，并得到图中所有电子的坐标数据，计算出这两幅图的h，m1处为h1，荧光屏处为h2，h的具体计算方法如下：
41.根据截面电子分布图中所有电子的坐标数据，采用散点轮廓算法(alpha shape)获取截面电子分布图的外部轮廓，如图2所示。统计轮廓上的点，求出各点到图中心的距离，取其平均值。
42.s3.保持l1,l2,l3,l4不变，测出h1,h2，取n1＝h2/h1，n1为电子注轴向截面的放大倍数；改变l3，上述数据测出6组，则l3,l4,h1,h2,n1均为一行6列的向量。对n1,l4进行高斯拟合，
得到对应的函数称为电子注截面有效增益函数，函数如式(1)，对应曲线如图3所示，定义域为[0,20]。
[0043]
general model gaussl:
[0044]
f(x)＝a1*exp(
‑
((x
‑
b1)/c1)^2)
[0045]
coefficients(with 95％confidence bounds):
[0046]
a1＝47.71 (
‑
22.97,118.4)
[0047]
b1＝8.11 (5.958,28.8)
[0048]
c1＝5.124 (0.6404,13.19)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0049]
goodness of fit:
[0050]
sse:0.3808
[0051]
r
‑
square:0.997
[0052]
adjusted r
‑
square:0.995
[0053]
rmse:0.3563
[0054]
式(1)中，a1,b1,c1为实常数，sse为和方差，越接近于0说明模型选择与拟合更好；r
‑
square为单变量确定系数，取值范围为[0，1]，越接近1则方程的变量对f(x)的解释能力越强，adjusted r
‑
square为多变量确定系数，rmse为均方根。
[0055]
在本步骤中，l3每次改变，电子注的z
w
和r
w
均会有微小变化，但模拟后发现变化量均小于0.001mm，故可认为该过程z
w
和r
w
此二者保持不变。则电子注截面有效增益函数可求出任意轴向位置处电子注半径和荧光屏处电子注半径之间的放大倍数。注腰位置z
w
为轴向电子注半径最小位置，因此电子注截面有效增益函数在电子注轴向上的第一个极大值点必在电子注的注腰位置附近。
[0056]
s4.将l3、z4恢复至步骤s3之前，测量荧光屏处的h'2，将l4代入电子注截面有效增益函数，求出此时m1与荧光屏处电子注半径的放大倍数n2,根据h'2与n2计算出此时m1处的h数据，设为h1'。
[0057]
z4前后移动6
‑
14范围内再取15个横截面，求出15个横截面相应的h数据，加上h1'构成一行16列的向量，并将16列的向量设为h3，将h3对应的轴坐标的向量设为z3，对其进行4阶的傅里叶拟合得到电子注包络函数，如公式(2),拟合曲线如图5。
[0058]
将实际的电子枪、电极片和荧光屏组装并抽真空。在真空度为1.0*10
‑6pa下固定各位置，进行电子注发射实验，在荧光屏处得到经过透镜组调制之后的电子注光斑。
[0059]
general model fourier4:
[0060]
f(x)＝a0+a1*cos(x*w)+b1*sin(x*w)+a2*cos(2*x*w)+b2*sin(2*x*w)
[0061]
+a3*cos(3*x*w)+b3*sin(3*x*w)+a4*cos(4*x*w)+b4*sin(4*x*w)
[0062]
coefficients(with 95％confidence bounds):
[0063]
a0＝0.3609(0.2184,0.5034)
[0064]
a1＝0.3468(0.1624,0.5312)
[0065]
b1＝
‑
0.03551(
‑
0.2392,0.1682)
[0066]
a2＝0.1132(0.07579,0.1506)
[0067]
b2＝
‑
0.03594(
‑
0.1739,0.1021)
[0068]
a3＝0.02207(0.0142,0.02993)
ꢀꢀꢀꢀꢀ
(2)
[0069]
b3＝
‑
0.0151(
‑
0.05749,0.02729)
[0070]
a4＝0.001715(
‑
0.00185,0.00528)
[0071]
b4＝
‑
0.002405(
‑
0.007208,0.002398)
[0072]
w＝0.2618(0.216,0.3076)
[0073]
goodness of fit:
[0074]
sse:2.624e
‑
13
[0075]
r
‑
square:1
[0076]
adjusted r
‑
square:1
[0077]
rmse:2.091e
‑
07
[0078]
变量介绍：w为误差余项，a0～b4为常系数，其余参量与式(1)意义相同。
[0079]
此过程仅仅选择了z4附近的横截面参与计算，并未移动m1，消除了移动电极片时注腰位置和注腰半径的变化，可降低计算误差。求出该函数在电子注轴向上的极小值和极小值点，即电子注的注腰半径和注腰位置。
[0080]
s5.求得函数式(2)在电子注轴向范围上的极小值和极小值点为0.1061mm，极小值点为11.9638mm，加上修正常量，即可求得注腰半径和注腰位置。
[0081]
经过s2
‑
s4的15次循环数据仿真、测量，得出以下结论：由4阶傅里叶拟合所得数据，注腰半径数值加上0.1mm，注腰位置减去3mm后，精度符合实际情况，与mtss软件模拟结果相比，注腰半径误差限在0.05mm，注腰位置误差限在0.05mm。则修正后的数据即为最终的电子注的注腰半径和注腰位置。本实施例中mtss所设计的电子枪，其模拟所得电子注注腰半径为0.2302mm,注腰位置为8.9624mm，模拟结果如图6
‑
图8所示，分别为电子注注腰半径收敛曲线、注腰位置收敛曲线，电子轨迹在yz平面的投影。而本实施例计算所得注腰半径为0.2069mm，注腰位置为8.9638mm，误差限极小。可见，本发明通过将电子注进行降压扩散处理，在保证电子注能量分布曲线的情况下，使之能够对高能量小半径电子注开展检测工作，分析电子注状态，指导空间行波管电子枪的设计工作，保障整管性能。