一种GNSS定位精度增强方法与流程

一种gnss定位精度增强方法
技术领域
1.本发明涉及卫星定位技术领域，具体涉及一种gnss定位精度增强方法。


背景技术：

2.全球导航卫星系统(gnss)通常指允许基于从多个gnss卫星接收的gnss信号来确定位置定位(positionfix)的系统。每一个gnss卫星传输gnss信号，该gnss信号标识信号传输的卫星和时间。gnss天线/接收器被配置为接收由可视gnss卫星传输的gnss信号中的每一个，并使用每一个gnss信号的飞行时间以及每一个gnss卫星的已知位置来确定从gnss天线/接收器到相应gnss卫星的伪距或距离。该多个所计算的伪距用于三边测量gnss天线/接收器在三维空间中的位置。gnss系统的类型包括全球定位系统(gps)、格洛纳斯(glonass)、伽利略(galileo)、北斗(bds)等。
3.现有技术cn202011024660.5公开了用于使用两个或更多个天线的位置定位估计的系统和方法，包括第一gnss天线/接收器、第二gnss天线/接收器和gnss处理器系统。该第一gnss天线/接收器位于第一位置处，并且基于所接收的gnss信号计算第一伪距。该第二gnss天线/接收器位于距该第一gnss天线/接收器已知距离的第二位置处，其中该第二gnss天线/接收器基于所接收的gnss信号计算第二伪距。该gnss处理器系统被配置为接收该第一伪距和该第二伪距，其中响应于该gnss处理器系统将该第一和第二伪距中的一个标识为错误的，并且将该第一和第二伪距中的一个标识为有效的，该gnss处理系统计算经校正的伪距并且使用该经校正的伪距和有效的该伪距来确定该第一gnss天线/接收器和该第二gnss天线/接收器的gnss位置定位估计，但是仅依赖于伪距数据依次筛选修正进行定位估计，数据粘合性高，一旦一个数据出错会造成定位估计失效，而且利用固定的数学函数进行定位解算难以完全匹配卫星定位数据间的映射关系，整体精度低且效率低。


技术实现要素：

4.本发明的目的在于提供一种gnss定位精度增强方法，以解决现有技术中仅依赖于伪距数据依次筛选修正进行定位估计，数据粘合性高，一旦一个数据出错会造成定位估计失效，而且利用固定的数学函数进行定位解算难以完全匹配卫星定位数据间的映射关系，整体精度低且效率低的技术问题。
5.为解决上述技术问题，本发明具体提供下述技术方案：
6.一种gnss定位精度增强方法，包括以下步骤：
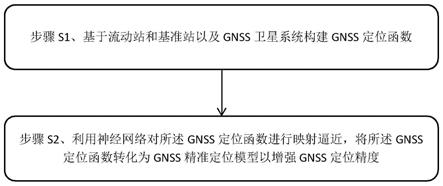
7.步骤s1、基于流动站和基准站以及gnss卫星系统构建gnss定位函数；
8.步骤s2、利用神经网络对所述gnss定位函数进行映射逼近，将所述gnss定位函数转化为gnss精准定位模型以增强gnss定位精度。
9.作为本发明的一种优选方案，所述步骤s1中，所述gnss定位函数的构建方法包括：
10.步骤s101、基于基准站和gnss卫星系统构建基准伪距观测方程，所述基准伪距观测方程表征为基准站到所述gnss卫星系统中所有卫星的伪距观测值，其中，所述基准伪距
观测方程为：
[0011][0012]
其中，b表征为基准站，j表征为卫星，为基准站至卫星j的伪距观测值，为基准站至卫星j的几何距离，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为基准站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差，(x
b
,y
b
,z
b
)为基准站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标；
[0013]
步骤s102、基于流动站和gnss卫星系统构建流动伪距观测方程，所述基准伪距观测方程表征为流动站到所述gnss卫星系统中所有卫星的伪距观测值，其中，所述流动伪距观测方程为：
[0014]
f2＝p
mj
＝ρ
mj
+δt
mj
+i
mj
+t
mj
+ε
mj
；
[0015]
其中，m表征为流动站，j表征为卫星，为流动站至卫星j的伪距观测值，为流动站至卫星j的几何距离，δt
mj
为流动站接收机与卫星的钟差矩阵参数，分别为流动站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差；
[0016]
步骤s103、基于所述基准伪距观测方程和流动伪距观测方程构建gnss定位函数，所述gnss定位函数表征为流动站的三维坐标与所述伪距观测值和gnss卫星系统中所有卫星的三维坐标的非线性映射关系。
[0017]
作为本发明的一种优选方案，所述步骤s101还包括对所述基准伪距观测方程进行修正得到伪距修正方程，所述伪距修正方程表征为基准站到所述gnss卫星系统中所有卫星的伪距修正值，其中，所述伪距修正方程为：
[0018]
δρ
bj
＝p
bj
‑
ρ
bj
＝δt
bj
+i
bj
+t
bj
+ε
bj
；
[0019]
其中，b表征为基准站，j表征为卫星，为基准站至卫星j的伪距观测值，为基准站至卫星j的几何距离，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为基准站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差，(x
b
,y
b
,z
b
)为基准站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标。
[0020]
作为本发明的一种优选方案，所述步骤s102还包括：
[0021]
基于所述伪距修正方程和流动伪距观测方程构建用于粗略确定流动站三维坐标的伪距定位方程，所述伪距定位方程为：
[0022][0023]
其中，m表征为流动站，j表征为卫星，为流动站至卫星j的伪距观测值，为流动站至卫星j的几何距离，δt
mj
为流动站接收机与卫星的钟差矩阵参数，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为流动站的电离层误差和对流层误差，为
伪距观测噪声及其他非模型化误差，(x
m
,y
m
,z
m
)为流动站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标。
[0024]
作为本发明的一种优选方案，所述步骤s103中，所述gnss定位函数的构建方法包括：
[0025]
设定b＝δt
mj
‑
δt
bj
，sv＝(x
m
,y
m
,z
m
)，u＝(x
j
,y
j
,z
j
)，pr＝p
mj
‑
δρ
bj
，er＝ε
mj
，将所述伪距定位方程g1进行等式代换，得到：
[0026]
pr＝|sv
‑
u|+b+er；
[0027]
将pr＝|sv
‑
u|+b+er转换为非线性映射函数形式，得到gnss定位函数为：
[0028]
sv＝f(u,pr)；
[0029]
式中，f表征为gnss定位函数的非线性映射函数体，sv表征为流动站的三维坐标，u表征为卫星j发射信号数据时刻卫星的三维坐标，pr表征为流动站和基准站的伪距关联值，b表征为流动站和基准站的钟差关联值，er表征为伪距观测噪声及其他非模型化误差。
[0030]
作为本发明的一种优选方案，所述步骤s2中，所述gnss精准定位模型的转化方法包括：
[0031]
步骤s201、搭建神经网络，并基于所述神经网络将所述gnss定位函数转化为神经网络模型形式；
[0032]
步骤s202、采集训练样本，并基于所述训练样本对所述神经网络进行模型训练得到所述gnss精准定位模型，实现利用所述伪距观测值和gnss卫星系统中所有卫星的三维坐标精准输出流动站的三维坐标。
[0033]
作为本发明的一种优选方案，所述步骤s201中，所述神经网络的搭建方法包括：
[0034]
基于gnss定位函数sv＝f(u,pr)将所述神经网络的输入设定为u和pr，输出设定为sv，其中，所述神经网络的输入形式为：
[0035]
{i
jt
|j∈[1,n],t∈[1,t]}，
[0036]
其中，u
t
表征为卫星j发射信号数据时刻t的三维坐标(x
jt
，y
jt
，z
jt
)，pr
t
表征为t时刻的流动站和基准站的伪距关联值p
mjt
‑
δρ
bjt
，t表征为时刻t的终值，n为gnss卫星系统中卫星总数；
[0037]
所述神经网络的输出形式为：{o
t
|t∈[1,t]}，
[0038]
其中，sv
t
表征为时刻t流动站的三维坐标(x
mt
，y
mt
，z
mt
)，t表征为时刻t的终值；
[0039]
所述神经网络的网络体设定为elm神经网络，隐藏层神经元设定为8500，神经元激活函数设定为sin函数，损失函数设定为均方根误差函数。
[0040]
作为本发明的一种优选方案，所述步骤s202中，所述训练样本的采集方法包括：
[0041]
在目标区域内均匀设置流动网格，并将基准站和流动站分布在所述流动网格内获
得在一段时间间隔内的流动站的三维坐标sv
t
，卫星j发射信号数据时刻卫星的三维坐标u
t
，以及流动站和基准站的伪距关联值pr
t
作为具有时序属性的训练样本[i
jt
,o
t
]。
[0042]
作为本发明的一种优选方案，将所述训练样本[i
jt
，o
t
]代入所述神经网络进行模型训练得到所述gnss精准定位模型。
[0043]
本发明与现有技术相比较具有如下有益效果：
[0044]
本发明利用融合gps卫星系统、bds卫星系统、glonass卫星系统和galileo卫星系统的gnss组合定位系统，可获得更多的可用卫星，改善了卫星的空间几何结构，从而提高了gnss卫星系统的可用性、可靠性和精确性，并对gnss卫星系统进行伪距差分定位获得对gnss接收器位置的定位函数，将定位函数利用神经网络进行非线性映射得到与卫星定位数据间的映射关系完全匹配的gnss精准定位模型，定位运算效率高、精度高。
附图说明
[0045]
为了更清楚地说明本发明的实施方式或现有技术中的技术方案，下面将对实施方式或现有技术描述中所需要使用的附图作简单地介绍。显而易见地，下面描述中的附图仅仅是示例性的，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图引伸获得其它的实施附图。
[0046]
图1为本发明实施例提供的gnss定位精度增强方法流程图；
[0047]
图2为本发明实施例提供的基准站和流动站在流动网格中的分布结构示意图。
具体实施方式
[0048]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0049]
如图1所示，基准站和流动站中均设置有gnss接收机，基准站和流动站中的gnss接收机同时接收由gps卫星系统、bds卫星系统、glonass卫星系统和galileo卫星系统的卫星信号数据构成的gnss卫星系统的所有卫星的卫星信号，同时融合gps卫星系统、bds卫星系统、glonass卫星系统和galileo卫星系统，可以获得更多可用的卫星进行定位，构建更为庞大的卫星空间结构，从而建立在庞大的卫星空间结构求得的gnss接收器位置的坐标更为精确，而且在gnss卫星系统的定位解算中所利用的线性解算函数，不能够完全匹配定位数据间的映射关系，因此本发明提供了一种gnss定位精度增强方法，利用神经网络进行大量数据训练得到与定位数据间的映射关系完全匹配的gnss精准定位模型，提高定位解算精度。
[0050]
本发明提供了一种gnss定位精度增强方法，包括以下步骤：
[0051]
步骤s1、基于流动站和基准站以及gnss卫星系统构建gnss定位函数；
[0052]
步骤s1中，gnss定位函数的构建方法包括：
[0053]
步骤s101、基于基准站和gnss卫星系统构建基准伪距观测方程，基准伪距观测方程表征为基准站到gnss卫星系统中所有卫星的伪距观测值，其中，基准伪距观测方程为：
[0054][0055]
其中，b表征为基准站，j表征为卫星，为基准站至卫星j的伪距观测值，为基准站至卫星j的几何距离，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为基准站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差，(x
b
,y
b
,z
b
)为基准站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标；
[0056]
步骤s101还包括对基准伪距观测方程进行修正得到伪距修正方程，伪距修正方程表征为基准站到gnss卫星系统中所有卫星的伪距修正值，其中，伪距修正方程为：
[0057]
δρ
bj
＝p
bj
‑
ρ
bj
＝δt
bj
+i
bj
+t
bj
+ε
bj
；
[0058]
其中，b表征为基准站，j表征为卫星，为基准站至卫星j的伪距观测值，为基准站至卫星j的几何距离，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为基准站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差，(x
b
,y
b
,z
b
)为基准站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标。
[0059]
步骤s102、基于流动站和gnss卫星系统构建流动伪距观测方程，基准伪距观测方程表征为流动站到gnss卫星系统中所有卫星的伪距观测值，其中，流动伪距观测方程为：
[0060]
f2＝p
mj
＝ρ
mj
+δt
mj
+i
mj
+t
mj
+ε
mj
；
[0061]
其中，m表征为流动站，j表征为卫星，为流动站至卫星j的伪距观测值，为流动站至卫星j的几何距离，δt
mj
为流动站接收机与卫星的钟差矩阵参数，分别为流动站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差；
[0062]
步骤s102还包括：
[0063]
基准站与流动站的电离层误差、对流层误差具有空间相关性，构建第一定位方程过程中保持基准站与流动站的对流层延迟和电离层延迟相等，即
[0064]
基于伪距修正方程和流动伪距观测方程构建用于粗略确定流动站三维坐标的伪距定位方程，伪距定位方程为：
[0065][0066]
其中，m表征为流动站，j表征为卫星，为流动站至卫星j的伪距观测值，为流动站至卫星j的几何距离，δt
mj
为流动站接收机与卫星的钟差矩阵参数，δt
bj
为基准站接收机与卫星的钟差矩阵参数，分别为流动站的电离层误差和对流层误差，为伪距观测噪声及其他非模型化误差，(x
m
,ym,z
m
)为流动站的三维坐标，(x
j
,y
j
,z
j
)为卫星j发射信号数据时刻卫星的三维坐标。
[0067]
上述步骤有效的量化了系统间偏差，可以有效减弱共性误差，增加观测量，提高参数求解的强度和性能；在通过系统差分原理构建gnss定位函数可以消除一些诸如卫星钟
差、基准站和流动站的接收机钟差、模型偏差等共性误差，最终提高了参数求解的模型强度和参数估计性能实现精准定位。
[0068]
步骤s103、基于基准伪距观测方程和流动伪距观测方程构建gnss定位函数，gnss定位函数表征为流动站的三维坐标与伪距观测值和gnss卫星系统中所有卫星的三维坐标的非线性映射关系。
[0069]
步骤s103中，gnss定位函数的构建方法包括：
[0070]
设定b＝δt
mj
‑
δt
bj
，sv＝(x
m
,y
m
,z
m
)，u＝(x
j
,y
j
,z
j
)，pr＝p
mj
‑
δρ
bj
，er＝ε
mj
，将伪距定位方程g1进行等式代换，得到：
[0071]
pr＝|sv
‑
u|+b+er；
[0072]
将pr＝|sv
‑
u|+b+er转换为非线性映射函数形式，得到gnss定位函数为：
[0073]
sv＝f(u,pr)；
[0074]
式中，f表征为gnss定位函数的非线性映射函数体，sv表征为流动站的三维坐标，u表征为卫星j发射信号数据时刻卫星的三维坐标，pr表征为流动站和基准站的伪距关联值，b表征为流动站和基准站的钟差关联值，er表征为伪距观测噪声及其他非模型化误差。
[0075]
pr＝|sv
‑
u|+b+er是连续且可微的函数，不存在闭合形式的解，而神经网络可以在训练样本充足的条件下无限逼近连续可微的函数，因此可利用将pr＝|sv
‑
u|+b+er函数转化为无限逼近定位数据间的映射关系的非线性映射函数形式sv＝f(u,pr)，即表征为sv，u，pr之间的数据关系可量化为具有某一固定形式的多为输入和输出的非线性映射，而f表征为gnss定位函数的非线性映射函数体，并没有具体的数学表达式，但却是连续可微的，利用神经网络基于sv＝f(u,pr)进行定位解算，能够比求解pr＝|sv
‑
u|+b+er获得更高的定位解算精度。
[0076]
步骤s2、利用神经网络对gnss定位函数进行映射逼近，将gnss定位函数转化为gnss精准定位模型以增强gnss定位精度。
[0077]
步骤s2中，gnss精准定位模型的转化方法包括：
[0078]
步骤s201、搭建神经网络，并基于神经网络将gnss定位函数转化为神经网络模型形式；
[0079]
步骤s202、采集训练样本，并基于训练样本对神经网络进行模型训练得到gnss精准定位模型，实现利用伪距观测值和gnss卫星系统中所有卫星的三维坐标精准输出流动站的三维坐标。
[0080]
步骤s201中，神经网络的搭建方法包括：
[0081]
基于gnss定位函数sv＝f(u,pr)将神经网络的输入设定为u和pr，输出设定为sv，其中，神经网络的输入形式为：
[0082]
{i
jt
|j∈[1,n],t∈[1,t]}，
[0083]
其中，u
t
表征为卫星j发射信号数据时刻t的三维坐标(x
jt
，y
jt
，z
jt
)，pr
t
表征为t时刻的流动站和基准站的伪距关联值p
mjt
‑
δρ
bjt
，t表征为时
刻t的终值，n为gnss卫星系统中卫星总数；
[0084]
神经网络的输出形式为：{o
t
|t∈[1，t]}，
[0085]
其中，sv
t
表征为时刻t流动站的三维坐标(x
mt
,y
mt
,z
mt
)，t表征为时刻t的终值；
[0086]
神经网络的网络体设定为elm神经网络，隐藏层神经元设定为8500，神经元激活函数设定为sin函数，损失函数设定为均方根误差函数。
[0087]
本实施例使用的elm神经网络，也可使用bp神经网络、ls网络等，均在本实施例的保护范围内。
[0088]
基于神经网络的原理，只要有足够多隐含层节点的神经网络可以以无限逼近非线性映射f，因此利用神经网络的方法，通过训练神经网络逼近非线性映射f，替代求解方程pr＝|sv
‑
u|+b+er的方法得到流动站的三维坐标，只需要在定位解算时，将观测值输入到由神经网络训练完成的gnss精准定位模型，即可得到流动站的三维坐标。
[0089]
如图2所示，步骤s202中，训练样本的采集方法包括：
[0090]
在目标区域内均匀设置流动网格，并将基准站和流动站分布在流动网格内获得在一段时间间隔内的流动站的三维坐标sv
t
，卫星j发射信号数据时刻卫星的三维坐标u
t
，以及流动站和基准站的伪距关联值pr
t
作为具有时序属性的训练样本[i
jt
,o
t
]。
[0091]
将训练样本[i
jt
,o
t
]代入神经网络进行模型训练得到gnss精准定位模型。
[0092]
本实施例在流动网络中设置基准站和流动站的数量不作限定，可由使用者进行自定义，在基准站和流动站的数量增加的同时，会使得gnss精准定位模型的精度得以提高，但同时也会神经网络的结构规模要求越高，因此在选择时需要进行精度和效率的权衡。
[0093]
本发明利用融合gps卫星系统、bds卫星系统、glonass卫星系统和galileo卫星系统的gnss组合定位系统，可获得更多的可用卫星，改善了卫星的空间几何结构，从而提高了gnss卫星系统的可用性、可靠性和精确性，并对gnss卫星系统进行伪距差分定位获得对gnss接收器位置的定位函数，将定位函数利用神经网络进行非线性映射得到与卫星定位数据间的映射关系完全匹配的gnss精准定位模型，定位运算效率高、精度高。
[0094]
以上实施例仅为本技术的示例性实施例，不用于限制本技术，本技术的保护范围由权利要求书限定。本领域技术人员可以在本技术的实质和保护范围内，对本技术做出各种修改或等同替换，这种修改或等同替换也应视为落在本技术的保护范围内。