一种BDS模糊度解算方法、装置、设备和存储介质与流程

一种bds模糊度解算方法、装置、设备和存储介质
技术领域
1.本发明涉及计算机技术领域，具体的说，涉及的是一种bds模糊度解算方法、装置、设备和存储介质。


背景技术：

2.中国北斗卫星导航系统(beidou navigation satellite system，bds)是中国自行研制的全球卫星导航系统，是为全球用户提供全天候、全天时、高精度的定位、导航和授时服务的基础设施，bds已经被广泛应用与交通运输、海洋渔业、气象预报和测绘地理信息等各个领域。
3.因受电离层、观测噪声等影响，bds在进行模糊度计算时会出现较大误差，因此需要降低电离层、观测噪声对模糊度计算的影响，bds高精度定位的核心问题在于如何准确地固定原始整周模糊度。


技术实现要素：

4.本发明实施例的目的是提供一种bds模糊度解算方法、装置、设备和存储介质，其能够根据预设的超宽巷组合、宽巷组合和窄巷组合，来依次计算双差超宽巷组合模糊度、双差宽巷组合模糊度及双差窄巷组合模糊度，进而计算得到原始载波整周模糊度，提高了模糊度计算的准确性和可靠性。
5.为实现上述目的，本发明实施例提供了一种bds模糊度解算方法，包括：
6.获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值；
7.根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；
8.根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，计算得到第一双差伪距观测值；
9.根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度；
10.根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，计算得到第二双差伪距观测值；
11.根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；
12.根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，解算得到原始载波整周模糊度。
13.作为上述方案的改进，所述超宽巷组合、所述宽巷组合，通过以下方式获得：
14.设置第一巷数的取值范围为第一巷数预设取值范围，设置第一电离层延迟放大系数的取值范围为第一电离层延时放大系数预设取值范围，设置第一噪声放大系数的取值范
围为第一噪声放大系数预设取值范围，设置第一组合系数之和为0；
15.根据所述第一巷数、所述第一电离层延迟放大系数、所述第一噪声放大系数，以及所述第一组合系数之和，计算获得若干第一候选组合、与所述第一候选组合对应的巷数、与所述第一候选组合对应的电离层延迟放大系数、与所述第一候选组合对应的噪声放大系数和与所述第一候选组合对应的三频组合波长；
16.根据与所述第一候选组合对应的巷数、与所述第一候选组合对应的电离层延迟放大系数、与所述第一候选组合对应的噪声放大系数和与所述第一候选组合对应的三频组合波长，将所有第一候选组合进行对比分析，从中选出两个第一候选组合分别作为超宽巷组合和宽巷组合。
17.作为上述方案的改进，所述窄巷组合，通过以下方式获得：
18.设置第二巷数的取值范围为第二巷数预设取值范围，设置第二电离层延迟放大系数的取值范围为第二离层延时放大系数预设取值范围，设置第二噪声放大系数的取值范围为第二噪声放大系数预设取值范围，设置第二组合系数之和为1；
19.根据所述第二巷数、所述第二电离层延迟放大系数、所述第二噪声放大系数，以及所述第二组合系数之和，计算获得若干第二候选组合、与所述第二候选组合对应的巷数、与所述第二候选组合对应的电离层延迟放大系数、与所述第二候选组合对应的噪声放大系数和与所述第二候选组合对应的三频组合波长；
20.根据与所述第二候选组合对应的巷数、与所述第二候选组合对应的电离层延迟放大系数、与所述第二候选组合对应的噪声放大系数和与所述第二候选组合对应的三频组合波长，将所有第二候选组合进行对比分析，从中选出窄巷组合。
21.作为上述方案的改进，所述第一巷数预设取值范围为[1，173]，所述第一电离层延时放大系数预设取值范围为(
‑
0.5，0.5)，所述第一噪声放大系数预设取值范围为[0，15]。
[0022]
作为上述方案的改进，所述第二巷数预设取值范围为[500，1500]，所述第二电离层延时放大系数预设取值范围为(
‑
0.3，0.3)，所述第二噪声放大系数预设取值范围为[0，10]。
[0023]
作为上述方案的改进，所述根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度，具体包括：
[0024]
根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差超宽巷组合模糊度。
[0025]
作为上述方案的改进，所述根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度，具体包括：
[0026]
根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差宽巷组合模糊度。
[0027]
作为上述方案的改进，所述根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度，具体包括：
[0028]
根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差窄巷组合模糊度。
[0029]
为实现上述目的，本发明实施例还提供了一种bds模糊度解算装置，包括：
[0030]
数据获取模块，用于获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组
合载波观测值和双差窄巷组合载波观测值；
[0031]
双差超宽巷组合模糊度解算模块，用于根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；
[0032]
第一双差伪距观测值计算模块，用于根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，计算得到第一双差伪距观测值；
[0033]
双差宽巷组合模糊度解算模块，用于根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度；
[0034]
第二双差伪距观测值计算模块，用于根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，计算得到第二双差伪距观测值；
[0035]
双差窄巷组合模糊度解算模块，用于根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；
[0036]
整周模糊度解算模块，用于根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，解算得到原始载波整周模糊度。
[0037]
为实现上述目的，本发明实施例还提供了一种bds模糊度解算设备，包括处理器、存储器以及存储在所述存储器中且被配置为由所述处理器执行的计算机程序，所述处理器执行所述计算机程序时实现如上述任一实施例所述的bds模糊度解算方法。
[0038]
为实现上述目的，本发明实施例还提供了一种计算机可读存储介质，所述计算机可读存储介质包括存储的计算机程序，其中，在所述计算机程序运行时控制所述计算机可读存储介质所在设备执行如上述任一实施例所述的bds模糊度解算方法。
[0039]
与现有技术相比，本发明实施例公开的一种bds模糊度解算方法、装置、设备和存储介质，通过获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值，以根据所述b3双差伪距值、预设的超宽巷组合和所述双差超宽巷组合载波观测值，来解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；通过根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，来计算得到第一双差伪距观测值；通过根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，来解算得到双差宽巷组合模糊度；通过根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，来计算得到第二双差伪距观测值；通过根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，来解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；进而根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，以解算得到原始载波整周模糊度。由此可见，本发明实施例能够根据预设的超宽巷组合、宽巷组合和窄巷组合，来依次计算双差超宽巷组合模糊度、双差宽巷组合模糊度及双差窄巷组合模糊度，进而计算得到原始载波整周模糊度，提高了模糊度计算的准确性和可靠性。
附图说明
[0040]
图1是本发明一实施例提供的一种bds模糊度解算方法的流程图；
[0041]
图2是本发明一实施例提供的一种bds模糊度解算装置的结构框图；
[0042]
图3是本发明一实施例提供的一种bds模糊度解算设备的结构框图。
具体实施方式
[0043]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0044]
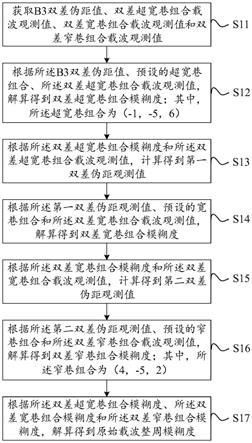
参见图1，是本发明一实施例提供的一种bds模糊度解算方法的流程图。
[0045]
所述bds模糊度解算方法可以由服务器执行，所述服务器可以ia架构服务器、risc架构服务器等不同类型的服务器；其中，所述服务器端具有高速的cpu运算能力、长时间的可靠运行、强大的i/o外部数据吞吐能力以及更好的扩展性，可以为各个领域提供定位类应用的响应服务请求、承担服务、保障服务。
[0046]
具体地，所述方法包括步骤s11～s17：
[0047]
s11、获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值；
[0048]
s12、根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；
[0049]
s13、根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，计算得到第一双差伪距观测值；
[0050]
s14、根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度；
[0051]
s15、根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，计算得到第二双差伪距观测值；
[0052]
s16、根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；
[0053]
s17、根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，解算得到原始载波整周模糊度。
[0054]
具体地，bds播发三个频率(b1、b2和b3)的载波信号，通过对原始的三个频率的载波观测值进行线性组合，形成新的组合观测量，以使形成的载波观测值具有长波长、弱电离层延迟、弱对流层延迟和低噪声的特点。bds载波观测值双差观测方程表示为：
[0055][0056]
其中，表示双差算子，例如表示双差载波观测值，表示双差站星距离，表示双差模糊度，表示双差电离层影响，表示双差对流层影响，表示双差噪声影响，和的单位都为m。
[0057]
1、确定双差超宽巷组合模糊度，并将其固定为整数：
[0058]
根据bds载波观测值双差观测方程，对公式(1)进行变形以应用于双差超宽巷组合模糊度的解算，超宽巷组合双差载波相位观测方程为：
[0059][0060]
其中，表示双差超宽巷组合载波观测值，表示双差超宽巷组合模糊度，λ
ewl
表示超宽巷组合波长，表示双差超宽巷组合电离层影响，表示双差对流层影响，表示双差超宽巷组合噪声影响。
[0061]
bds的b3载波上播放的是p码，以b3双差伪距值结合超宽巷组合(
‑
1，
‑
5，6)，解算双差超宽巷组合模糊度的浮点解：
[0062][0063]
其中，表示b3双差伪距值，表示超宽巷组合电离层放大系数，表示b3载波电离层放大系数，表示双差b1电离层影响，表示双差b3噪声影响，和皆为预先获取或预先设置的参数。
[0064]
对求解得到的双差超宽巷组合模糊度的浮点解进行取整对求解得到的双差超宽巷组合模糊度的浮点解进行取整得到为整数解的双差超宽巷组合模糊度，公式(3)中忽略了电离层残差以及其他误差的影响，在短基线条件下，由于超宽巷组合的波长较长，取整后仍可以获得准确的双差超宽巷组合模糊度的整数解。
[0065]
2、确定双差宽巷组合模糊度，并将其固定为整数：
[0066]
预设宽巷组合为(1，
‑
1，0)，根据计算得到的双差超宽巷组合模糊度和预先获取的双差超宽巷组合载波观测值，精准计算得到第二双差伪距值：
[0067][0068]
其中，表示第二双差伪距值。
[0069]
根据bds载波观测值双差观测方程，对公式(1)进行变形以应用于双差宽巷组合模糊度的解算，宽巷组合双差载波相位观测方程为：
[0070][0071]
其中，表示双差宽巷组合载波观测值，表示双差宽巷组合模糊度，λ
wl
表示宽巷组合波长，表示双差宽巷组合电离层影响，表示双差宽巷组合噪声影响。
[0072]
根据第一双差伪距观测值和宽巷组合(1，
‑
1，0)，解算双差宽巷组合模糊度的浮点解：
[0073][0074]
其中，表示宽巷组合电离层放大系数。
[0075]
对求解得到的双差宽巷组合模糊度的浮点解进行取整得到为整数解的双差宽巷组合模糊度。
[0076]
3、确定双差窄巷组合模糊度，并将其固定为整数：
[0077]
预设窄巷组合为(4，
‑
5，2)，根据计算得到的双差宽巷组合模糊度和预先
获取的双差宽巷组合载波观测值，精准计算得到第三双差伪距值：
[0078][0079]
其中，表示第三双差伪距值。
[0080]
根据bds载波观测值双差观测方程，对公式(1)进行变形以应用于双差窄巷组合模糊度的解算，窄巷组合双差载波相位观测方程为：
[0081][0082]
其中，表示双差窄巷组合载波观测值，表示双差窄巷组合模糊度，λ
nl
表示窄巷组合波长，表示双差窄巷组合电离层影响，表示双差窄巷组合噪声影响。
[0083]
根据第二双差伪距观测值和窄巷组合(4，
‑
5，2)，解算双差窄巷组合模糊度的浮点解：
[0084][0085]
其中，表示窄巷组合电离层延迟放大系数。
[0086]
对求解得到的双差窄巷组合模糊度的浮点解进行取整得到为整数解的双差窄巷组合模糊度
[0087]
4、原始载波整周模糊度的解算：
[0088]
根据以下公式计算原始载波整周模糊度：
[0089][0090]
其中，(a
e
，b
e
，c
e
)为超宽巷组合(
‑
1，
‑
5，6)，(a
w
，b
w
，c
w
)为宽巷组合(1，
‑
1，0)，(a
n
，b
n
，c
n
)为窄巷组合(4，
‑
5，2)。
[0091]
在本实施例中，通过获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值，以根据所述b3双差伪距值、预设的超宽巷组合和所述双差超宽巷组合载波观测值，来解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；通过根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，来计算得到第一双差伪距观测值；通过根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，来解算得到双差宽巷组合模糊度；通过根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，来计算得到第二双差伪距观测值；通过根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，来解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；进而根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，以解算得到原始载波整周模糊度。由此可见，本发明实施例能够根据预设的超宽巷组合、宽巷组合和窄巷组合，来依次计算双差超宽巷组合模糊度、双差宽巷组合模糊度及双差窄巷组合模糊度，进而计算得到原始载波整周模糊度，提高了模糊度计算的准确性和可靠性。
[0092]
在一种实施方式中，所述超宽巷组合和所述宽巷组合，通过以下方式获得，包括步
骤s111～s113：
[0093]
s111、设置第一巷数的取值范围为第一巷数预设取值范围，设置第一电离层延迟放大系数的取值范围为第一电离层延时放大系数预设取值范围，设置第一噪声放大系数的取值范围为第一噪声放大系数预设取值范围，设置第一组合系数之和为0；
[0094]
s112、根据所述第一巷数、所述第一电离层延迟放大系数、所述第一噪声放大系数，以及所述第一组合系数之和，计算获得若干第一候选组合、与所述第一候选组合对应的巷数、与所述第一候选组合对应的电离层延迟放大系数、与所述第一候选组合对应的噪声放大系数和与所述第一候选组合对应的三频组合波长；
[0095]
s113、根据与所述第一候选组合对应的巷数、与所述第一候选组合对应的电离层延迟放大系数、与所述第一候选组合对应的噪声放大系数和与所述第一候选组合对应的三频组合波长，将所有第一候选组合进行对比分析，从中选出两个第一候选组合分别作为超宽巷组合和宽巷组合。
[0096]
进一步地，在一种实施方式中，所述第一巷数预设取值范围为[1，173]，所述第一电离层延时放大系数预设取值范围为(
‑
0.5，0.5)，所述第一噪声放大系数预设取值范围为[0，15]。
[0097]
具体地，长波长、弱电离层、低噪声的bds三频载波观测值组合利于整周模糊度的解算，也便于周跳探测与修复。设置第一巷数的取值范围为[1，173]，设置第一电离层延迟放大系数的取值范围为(
‑
0.5，0.5)，设置第一噪声放大系数的取值范围为[0，15]，设置第一组合系数之和为0；根据第一巷数、第一电离层延迟放大系数、第一噪声放大系数，以及第一组合系数之和，计算获得若干第一候选组合(a，b，c)、与所述第一候选组合对应的巷数f
abc
、与所述第一候选组合对应的电离层延迟放大系数i
p
、与所述第一候选组合对应的噪声放大系数e
abc
^0.5和与所述第一候选组合对应的三频组合波长λ
abc
，具体数值参见表1：
[0098]
f
abc
abci
p
λ
abc
/me
abc
^0.57
‑1‑
56
‑
0.08220.9327.8741629
‑
110.1029.15814.3532314
‑
50.0206.3716.481300
‑
11
‑
0.0634.8841.41437
‑1‑
67
‑
0.1453.9609.2745313
‑4‑
0.0432.7655.09967
‑1‑
78
‑
0.2072.18710.6777627
‑9‑
0.0231.92811.5768312
‑3‑
0.1061.7653.74297
‑1‑
89
‑
0.2701.51112.08311311
‑2‑
0.1681.2972.450127
‑1‑
910
‑
0.3331.15413.49113625
‑7‑
0.1481.0778.83214310
‑1‑
0.2311.0251.414157
‑1‑
1011
‑
0.3950.93314.9001731
‑
10
‑
0.2930.8471.414
[0099]
从表1可看出，随着第一巷数的逐渐增大，三频组合波长逐渐减小，但是由于预先设置的第一巷数小于173，所以组合后的波长仍大于bds单频最大波长。上述第一候选组合对应的电离层延迟放大系数的绝对值均小于0.5，具有较好的抗电离层影响效果，有利于弱化基线距离的影响；组合后的载波观测值以周为单位的噪声放大系数均小于15。由于电离层延迟误差在长基线载波测量中不可忽视，因此从表1中选取电离层延迟放大系数的绝对值小于0.1的组合，在选出的第一候选组合中对比分析其组合特性(噪声放大系数、三频组合波长以及巷数)，最终选出(
‑
1，
‑
5，6)作为超宽巷组合，替换掉传统的超宽巷组合(0，
‑
1，1)，(1，
‑
1，0)作为宽巷组合。
[0100]
在一种实施例中，所述窄巷组合，通过以下方式获得，包括步骤s121～s123：
[0101]
s121、设置第二巷数的取值范围为第二巷数预设取值范围，设置第二电离层延迟放大系数的取值范围为第二离层延时放大系数预设取值范围，设置第二噪声放大系数的取值范围为第二噪声放大系数预设取值范围，设置第二组合系数之和为1；
[0102]
s122、根据所述第二巷数、所述第二电离层延迟放大系数、所述第二噪声放大系数，以及所述第二组合系数之和，计算获得若干第二候选组合、与所述第二候选组合对应的巷数、与所述第二候选组合对应的电离层延迟放大系数、与所述第二候选组合对应的噪声放大系数和与所述第二候选组合对应的三频组合波长；
[0103]
s123、根据与所述第二候选组合对应的巷数、与所述第二候选组合对应的电离层延迟放大系数、与所述第二候选组合对应的噪声放大系数和与所述第二候选组合对应的三频组合波长，将所有第二候选组合进行对比分析，从中选出窄巷组合。
[0104]
进一步地，在一种实施方式中，所述第二巷数预设取值范围为[500，1500]，所述第二电离层延时放大系数预设取值范围为(
‑
0.3，0.3)，所述第二噪声放大系数预设取值范围为[0，10]。
[0105]
具体地，设置第二巷数的取值范围为[500，1500]，设置第二电离层延迟放大系数的取值范围为(
‑
0.3，0.3)，设置第二噪声放大系数的取值范围为[0，10]，设置第二组合系数之和为1；根据第二巷数、第二电离层延迟放大系数、第二噪声放大系数，以及第二组合系数之和，计算获得若干第二候选组合(a，b，c)、与所述第二候选组合对应的巷数f
abc
、与所述第二候选组合对应的电离层延迟放大系数i
p
、与所述第二候选组合对应的噪声放大系数e
abc
^0.5和与所述第二候选组合对应的三频组合波长λ
abc
，具体数值参见表2：
[0106]
f
abc
abci
p
λ
abc
/me
abc
^0.55900101.2930.2481.0006200011.2310.2361.0007631001.0000.1921.00012224
‑1‑
20.2460.1204.58312293
‑
640.1630.1197.810124553
‑
70.2650.1189.11012524
‑2‑
10.1830.1174.58312593
‑
750.1010.1169.110127552
‑
60.2030.1158.06212824
‑
300.1200.1145.000
130551
‑
50.1400.1127.14113124
‑
410.0580.1125.745133550
‑
40.7740.1106.40313424
‑
52
‑
0.0050.1096.70813655
‑1‑
30.0150.1075.91613724
‑
63
‑
0.0670.1077.81013955
‑2‑2‑
0.0480.1055.74514024
‑
74
‑
0.1300.1059.000141862
‑7‑
0.0280.1039.434
[0107]
从表2可看出，第二候选组合(4，
‑
5，2)的电离层延迟放大系数最小，且噪声放大系数也很小，适用于长基线模糊度解算，因此，从表2中选出(4，
‑
5，2)作为窄巷组合。在长基线条件下，由于测站间空间相关性弱，电离层延迟和对流层延迟经过双差并不能很好的消除，对窄巷组合的影响尤为明显，在通过bds三频组合优化选取后，选取(
‑
1，
‑
5，6)代替传统的(0，
‑
1，1)宽巷组合，选择弱电离层几何相位组合(4，
‑
5，2)代替传统的窄巷组合(0，0，1)，使得模糊度的解算更加精准。
[0108]
在一种实施方式中，步骤s12中的所述根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度，具体包括：
[0109]
根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差超宽巷组合模糊度。
[0110]
在一种实施方式中，步骤s14中的所述根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度，具体包括：
[0111]
根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差宽巷组合模糊度。
[0112]
在一种实施方式中，步骤s16中的所述根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度，具体包括：
[0113]
根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，利用载波相位平滑伪距算法，解算得到双差窄巷组合模糊度。
[0114]
可选的，载波相位平滑伪距算法为hatch滤波，其原理为：
[0115]
通过相位平滑伪距，消除电离层一阶巷的影响：
[0116]
其中，表示p卫星在j历元时刻的伪距平滑值，表示p卫星在j历元时刻的伪距观测值，表示j历元与j
‑
1历元时刻的载波相位差。
[0117]
综上所述，与现有技术相比，本发明实施例公开的bds模糊度解算方法，能够根据预设的超宽巷组合、宽巷组合和窄巷组合，来依次计算双差超宽巷组合模糊度、双差宽巷组合模糊度及双差窄巷组合模糊度，进而计算得到原始载波整周模糊度，提高了模糊度计算的准确性和可靠性。
[0118]
为便于理解bds三频组合观测量相关特性的理解，以下进行原理介绍：
[0119]
将原始的不同频率载波观测值线性组合形成新的组合观测量，组合后的载波观测
值具备以下特点：长波长、弱电离层延迟、弱对流层延迟和低噪声，为周跳检验量的选取提供了更多选择，提高了周跳探测的精度和灵敏度，提高了模糊度解算效率和精度。
[0120]
北斗卫星以m为单位的载波相位观测方程为(只考虑电离层延迟一阶项影响)：
[0121][0122]
令ξ＝t+c(δt
u
‑
δt
s
)+m，表示非色散性误差，则式(11)可简化为：
[0123][0124]
其中，l
i
表示载波i的载波相位观测值，单位为m；ρ表示接收机天线相位中心到卫星天线相位中心的几何距离；λ
i
为载波i的载波波长；n
i
为载波i的载波整周模糊度；i
b1
表示b1载波的电离层延迟，单位为m；q
i
为载波i的电离层比例因子；ξ表示对流层延迟、接收机钟差、卫星钟差、多路径效应等非色散性误差，单位为m；ε
m
表示载波观测噪声，单位为m；根据电离层延迟的色散效应，q
i
＝(f
b1
/f
bi
)2，i＝1，2，3，即q1＝1，q2＝1.672，q3＝1.514。
[0125]
假设原始组合系数为u，v，w，则组合后以m为单位的载波观测方程为：
[0126]
l
b
[m]＝ul1+vl2+wl3＝(u+v+w)(ρ+ξ)
‑
n
b
λ
b
‑
(uq1+vq2+wq3)i
b1
+ε
b
；
ꢀꢀ
(13)
[0127]
n
b
λ
b
＝uλ1n1+vλ2n2+wλ3n3，ε
b
＝uε
m1
+vε
m2
+wε
m3
；
ꢀꢀ
(14)
[0128]
其中，l
b
为组合后的以m为单位的载波相位观测值，λ
b
表示组合后的波长，n
b
表示组合后的整周模糊度，对公式(14)进行变形，得到：
[0129]
n
b
＝(uλ1/λ
b
)n1+(vλ2/λ
b
)n2+(wλ3/λ
b
)n3；
ꢀꢀ
(15)
[0130]
鉴于整周模糊度的整数特性，这里定义新的组合(a，b，c)：
[0131]
a＝uλ1/λ
b
，b＝vλ2/λ
b
，c＝wλ3/λ
b
；
ꢀꢀ
(16)
[0132]
将公式(16)代入公式(13)，得到以周为单位的组合观测方程：
[0133][0134]
其中，为以周为单位的组合后的载波相位观测值，由公式(17)可知，组合后的整周模糊度n
b
＝n(a，b，c)＝an1+bn2+cn3，对应的组合频率为f
b
＝f(a，b，c)＝af
b1
+bf
b2
+cf
b3
。设f0为北斗卫星基准频率，则f0＝2.046mhz，由此得到f
bi
＝k
i
f0，(i＝1，2，3)，k1＝763，k2＝590，k3＝620，将k
i
的具体取值代入组合频率的计算，得到：
[0135]
f
b
＝af
b1
+bf
b2
+cf
b3
＝f0(763a+590b+620c)；
ꢀꢀ
(18)
[0136]
令k＝763a+590b+620c，将其定义为巷数f
abc
，因为a，b，c是整数，存在：
[0137]
ak1+bk2+ck3＝f
abc
gcd(k1，k2，k3)；
ꢀꢀ
(19)
[0138]
其中，gcd(k1，k2，k3)表示括号内k1，k2，k3三个数的最大公约数，f
abc
是由a，b，c决定的整数；由于bds的gcd(k1，k2，k3)＝1，则组合后的波长可表示为：λ
b
＝c’/f
b
＝λ0/k＝λ0/f
abc
，λ0＝c’/f0≈146.526m，c’表示真空中的光速。由此可知，bds三频组合载波观测值的波长和频率与f
abc
值的大小有关系。
[0139]
电离层延迟的分析：
[0140]
组合后的以m为单位的电离层延迟放大系数为：
[0141][0142]
其中，i
p
表示电离层延迟放大系数；根据电离层延迟的色散效应，q
i
可表示为：q
i
＝
(f
b1
/f
bi
)2，i＝1，2，3。代入b1、b2、b3所示频率，得到：q1＝1，q2＝1.672，q3＝1.514。将公式(20)的两边同乘以λ1/λ
b
，即得到组合后的以周为单位的电离层延迟放大系数：
[0143][0144]
令这样就消除了组合后的电离层延迟影响。同时，也在以a，b，c为基向量建立的三维空间坐标系内定义了一个平面，在该平面内的所有组合系数(a，b，c)都对应一个无电离层延迟的组合，三维坐标系中的组合系数(a，b，c)作为一个空间点越靠近这个平面，其电离层延迟越小。
[0145]
将公式(21)进行变形，得：
[0146][0147]
同样，由整数线性方程解存在理论，得：
[0148]
k2k3a+k1k3b+k1k2c＝i
abc
gcd(k2k3，k1k3，k1k2)；
ꢀꢀ
(23)
[0149]
其中，bds的gcd(k2k3，k1k3，k1k2)＝10，根据a，b，c取值的不同，i
abc
取值不同，电离层延迟影响系数应该是的整数倍，的大小由i
abc
的取值直接决定，i
abc
表示为电离层数。如果：
[0150][0151]
则，组合后的电离层延迟误差小于b1载波上的电离层延迟误差，当i
abc
＝0时，电离层影响消除。
[0152]
对流层延时分析：
[0153]
对流层延迟属于非色散性误差，与载波频率无关，其线性组合放大系数为：
[0154][0155]
其中，c’为真空中的光速。令则以a，b，c为基向量建立的三维空间坐标系内定义了一个无对流层延迟平面，组合系数(a，b，c)作为一个空间点越靠近这个平面，对应组合的对流层延迟越小。由于对流层延迟的非色散性，无对流层延迟组合等价于无几何相位(geo
‑
free)组合，不仅消除了对流层延迟影响，而且也消除了如接收机钟差、卫星星历误差、卫星钟差和卫星轨道误差等其他非色散性误差。
[0156]
观测噪声的分析：
[0157]
设σ
b1
、σ
b2
、σ
b3
分别表示三个频率的载波测量值的噪声标准差(单位：周)。
[0158]
假定它们相等且相互独立，即
[0159]
根据误差传播定律，得：
[0160][0161]
其中，表示组合后的噪声标准差，令e
abc
＝a2+b2+c2，则公式(26)化简为：由于e
abc
是整数，所以组合后以周为单位的载波观测值噪声大于单个载波观测值噪声，表示噪声放大系数。
[0162]
以a，b，c为基向量建立的三维空间坐标系内定义了一条直线：
[0163][0164]
组合系数(a，b，c)作为一个空间点越靠近这条直线，减少观测噪声的效率就越高。
[0165]
bds三频组合的选取标准：
[0166]
(1)组合系数a，b，c为整数；
[0167]
(2)组合波长较长，便于周跳探测与整周模糊度解算；
[0168]
(3)弱电离层延迟，消弱基线距离的影响；
[0169]
(4)组合后的噪声较小。
[0170]
影响载波观测值质量的主要误差源随基线长度增加并不同，在长基线测量中，由于基站间空间相关性弱，大气延迟误差如电离层延迟、对流层延迟经过差分并不能很好的消除，此时，组合系数(a，b，c)作为一个空间点应该优先靠近无电离层延迟平面和无对流层延迟平面；当基线较短时(≤20km)，基站间空间相关性强，差分后基本消除大气延迟误差，误差源以观测误差为主，针对这种情况，组合系数(a，b，c)作为一个空间点应该优先靠近原点。根据实际应用情况，以影响观测数据质量的主要误差源来决定组合系数的选取。
[0171]
短基线条件下，为了减弱观测噪声和电离层延迟的影响，组合系数(a，b，c)作为一个空间点应接近：
[0172]
(1)无电离层延迟平面；
[0173]
(2)最大限度减小观测噪声影响的空间直线。
[0174]
下面以整数线性变换理论为基础，从消弱电离层延迟和观测噪声的角度出发，筛选优秀的组合系数。
[0175]
根据上述原则，由公式(9)和公式(13)，可得：
[0176][0177]
其中g1＝gcd(k1，k2，k3)，g2＝gcd(k2k3，k1k3，k1k2)。当a，b，c确定后，f
abc
、i
abc
值随着确定，但是不能从f
abc
、i
abc
推导出a，b，c。为了从给定的f
abc
、i
abc
所有a，b，c
α，b，c
组合中寻找噪声e
abc
最小的组合，需要给组合系数定义新的关系：
[0178]
令s1a+s2b+s3c＝s
abc
(gcd(s1，s2，s3)＝1)，则有：
[0179][0180]
若det z≠0，通过公式(29)，可得：
[0181][0182]
其中中，z
*
表示z的伴随矩阵，det z表示z的行列式，l、i、s分别为z
*
的1、2、3列。若det z＝
±
1，则c和c
z
之间存在一一对应的整数线性关系；若det z≠
±
1，则f
abc
、i
abc
、s
abc
取值应满足gcd[(lf
abc
+ii
abc
+ss
abc
)
t
]＝
±
det z。
[0183]
将bds的k1、k2、k3、g1和g2的具体数值代入z中，得：
[0184][0185]
可以得到z的行列式det z＝
‑
2769690s1‑
11668371s2+14512278s3，由于gcd(2769690，11668371，14512278)＝33≠1，所以不存在s1、s2、s3线性组合使得c和c
z
之间一一对应的整数线性关系成立，因此对s1、s2、s3简单赋值，s1＝1，s2＝1，s3＝1，a+b+c＝s
abc
，得到：
[0186][0187]
通过一定的巷数f
abc
、电离层数i
abc
、合适的s
abc
可以得到确定的a，b，c，而实际需要的是在给定f
abc
、i
abc
取值的条件下，e
abc
最小的系数组合。令h＝lf
abc
+ii
abc
，由公式(30)可知：
[0188][0189]
将公式(31)对s
abc
求导，得到令得到：
[0190][0191]
其中，为巷数f
abc
和电离层数i
abc
给定的情况下使噪声影响系数e
abc
最小的s
abc
值。s
abc
还应满足式gcd[(lf
abc
+ii
abc
+ss
abc
)
t
]＝
±
det z。代入具体数据，得：
[0192][0193]
当波长较长时f
abc
较小，同时为了减弱电离层延迟，可得因此，组合后波长较长、电离层影响较小、噪声影响较弱的组合，其组合系数之和为0。
[0194]
将公式(33)进行变形，得：
[0195][0196]
电离层误差较小、噪声值最优的宽巷和超宽巷组合，其组合系数之和为0；电离层延迟较小、噪声最优的窄巷组合，其组合系数之和为1。
[0197]
参见图2，是本发明一实施例提供的一种bds模糊度解算装置的结构示意图。bds模糊度解算装置10，包括：
[0198]
数据获取模块11，用于获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值；
[0199]
双差超宽巷组合模糊度解算模块12，用于根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；
[0200]
第一双差伪距观测值计算模块13，用于根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，计算得到第一双差伪距观测值；
[0201]
双差宽巷组合模糊度解算模块14，用于根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度；
[0202]
第二双差伪距观测值计算模块15，用于根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，计算得到第二双差伪距观测值；
[0203]
双差窄巷组合模糊度解算模块16，用于根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；
[0204]
整周模糊度解算模块17，用于根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，解算得到原始载波整周模糊度。
[0205]
值得说明的是，具体的所述bds模糊度解算装置10的工作过程可参考上述实施例中所述bds模糊度解算方法的工作过程，在此不再赘述。
[0206]
在本实施例中，bds模糊度解算装置10通过获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值，以根据所述b3双差伪距值、预设的超宽巷组合和所述双差超宽巷组合载波观测值，来解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；通过根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，来计算得到第一双差伪距观测值；通过根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，来解算得到双差宽巷组合模糊度；通过根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，来计算得到第二双差伪距观测值；通过根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，来解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；进而根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，以解算得到原始载波整周模糊度。由此可见，本发明实施例能够根据预设的超宽巷组合、宽巷组合和窄巷组合，来依次计算双差超宽巷组合模糊度、双差宽巷组合模糊度及双差窄巷组合模糊度，进而计算得到原始载波整周模糊度，提高了模糊度计算的准确性和可靠性。
[0207]
值得说明的是，具体的所述bds模糊度解算装置10的工作过程可参考上述实施例中所述bds模糊度解算方法的工作过程，在此不再赘述。
[0208]
参见图3，是本发明实施例提供的一种bds模糊度解算设备20，包括处理器21、存储器22以及存储在所述存储器22中且被配置为由所述处理器21执行的计算机程序，所述处理器21执行所述计算机程序时实现如上述bds模糊度解算方法实施例中的步骤，例如图1中所述的步骤s11～s17；或者，所述处理器21执行所述计算机程序时实现上述各装置实施例中各模块的功能，例如数据获取模块11。
[0209]
示例性的，所述计算机程序可以被分割成一个或多个模块，所述一个或者多个模
块被存储在所述存储器22中，并由所述处理器21执行，以完成本发明。所述一个或多个模块可以是能够完成特定功能的一系列计算机程序指令段，该指令段用于描述所述计算机程序在所述bds模糊度解算设备20中的执行过程。例如，所述计算机程序可以被分割成多个模块，各模块具体功能如下：
[0210]
数据获取模块11，用于获取b3双差伪距值、双差超宽巷组合载波观测值、双差宽巷组合载波观测值和双差窄巷组合载波观测值；
[0211]
双差超宽巷组合模糊度解算模块12，用于根据所述b3双差伪距值、预设的超宽巷组合、所述双差超宽巷组合载波观测值，解算得到双差超宽巷组合模糊度；其中，所述超宽巷组合为(
‑
1，
‑
5，6)；
[0212]
第一双差伪距观测值计算模块13，用于根据所述双差超宽巷组合模糊度和所述双差超宽巷组合载波观测值，计算得到第一双差伪距观测值；
[0213]
双差宽巷组合模糊度解算模块14，用于根据所述第一双差伪距观测值、预设的宽巷组合和所述双差宽巷组合载波观测值，解算得到双差宽巷组合模糊度；
[0214]
第二双差伪距观测值计算模块15，用于根据所述双差宽巷组合模糊度和所述双差宽巷组合载波观测值，计算得到第二双差伪距观测值；
[0215]
双差窄巷组合模糊度解算模块16，用于根据所述第二双差伪距观测值、预设的窄巷组合和所述双差窄巷组合载波观测值，解算得到双差窄巷组合模糊度；其中，所述窄巷组合为(4，
‑
5，2)；
[0216]
整周模糊度解算模块17，用于根据所述双差超宽巷组合模糊度、所述双差宽巷组合模糊度和所述双差窄巷组合模糊度，解算得到原始载波整周模糊度。
[0217]
各个模块具体的工作过程可参考上述实施例所述的bds模糊度解算装置10的工作过程，在此不再赘述。
[0218]
所述bds模糊度解算设备20可以是桌上型计算机、笔记本、掌上电脑及云端服务器等计算设备。所述bds模糊度解算设备20可包括，但不仅限于，处理器21、存储器22。本领域技术人员可以理解，所述示意图仅仅是bds模糊度解算设备的示例，并不构成对bds模糊度解算设备20的限定，可以包括比图示更多或更少的部件，或者组合某些部件，或者不同的部件，例如所述bds模糊度解算设备20还可以包括输入输出设备、网络接入设备、总线等。
[0219]
所述处理器21可以是中央处理单元(central processing unit，cpu)，还可以是其他通用处理器、数字信号处理器(digital signal processor，dsp)、专用集成电路(application specific integrated circuit，asic)、现成可编程门阵列(field
‑
programmable gate array，fpga)或者其他可编程逻辑器件、分立门或者晶体管逻辑器件、分立硬件组件等。通用处理器可以是微处理器或者该处理器也可以是任何常规的处理器等，所述处理器21是所述bds模糊度解算设备20的控制中心，利用各种接口和线路连接整个bds模糊度解算设备20的各个部分。
[0220]
所述存储器22可用于存储所述计算机程序和/或模块，所述处理器21通过运行或执行存储在所述存储器22内的计算机程序和/或模块，以及调用存储在存储器22内的数据，实现所述bds模糊度解算设备20的各种功能。所述存储器22可主要包括存储程序区和存储数据区，其中，存储程序区可存储操作系统、至少一个功能所需的应用程序等；存储数据区可存储根据设备的使用所创建的数据等。此外，存储器22可以包括高速随机存取存储器，还
可以包括非易失性存储器，例如硬盘、内存、插接式硬盘，智能存储卡(smart media card,smc)，安全数字(secure digital,sd)卡，闪存卡(flash card)、至少一个磁盘存储器件、闪存器件、或其他易失性固态存储器件。
[0221]
其中，所述bds模糊度解算设备20集成的模块如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明实现上述实施例方法中的全部或部分流程，也可以通过计算机程序来指令相关的硬件来完成，所述的计算机程序可存储于一计算机可读存储介质中，该计算机程序在被处理器执行时，可实现上述各个方法实施例的步骤。其中，所述计算机程序包括计算机程序代码，所述计算机程序代码可以为源代码形式、对象代码形式、可执行文件或某些中间形式等。所述计算机可读介质可以包括：能够携带所述计算机程序代码的任何实体或装置、记录介质、u盘、移动硬盘、磁碟、光盘、计算机存储器、只读存储器(rom，read
‑
only memory)、随机存取存储器(ram，random access memory)、电载波信号、电信信号以及软件分发介质等。
[0222]
本领域普通技术人员可以理解实现上述实施例方法中的全部或部分流程，是可以通过计算机程序来指令相关的硬件来完成，所述的程序可存储于一计算机可读取存储介质中，该程序在执行时，可包括如上述各方法的实施例的流程。其中，所述的存储介质可为磁碟、光盘、只读存储记忆体(read
‑
onlymemory，rom)或随机存储记忆体(randomaccessmemory，ram)等。
[0223]
以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。