一种基于假想源的二次定位计算的微地震定位方法

1.本发明属于微地震震源定位技术领域，具体涉及一种基于假想源的二次定位计算的微地震定位方法。


背景技术：

2.地震震源定位可以划分为两个时期，以1912年geiger的开拓性工作为界线，之前是几何作图法，包括单台资料法和多台资料法，单台资料法包括方位角法和出射角法，多台资料法包括虚波速度法、虚拟法、交切法、引中线法、和达法和高桥法等方法，几何作图法都是通过震中所在轨迹线的相交，确定震中位置，其定位精度低。1912年geiger开拓性工作之后为数字定位法，1975年lee等利用geiger理论，实现了震源定位程序，连续给出了hypo71-86系列程序。考虑到台站位置以及速度结构对定位的影响，发展了联合定位方法，震源位置和台站校正的联全定位方法(jed，jhd)，震源位置与速度结构联合反演方法(ssh)，由jed方法还发展出来了主事件定位方法(atd)。2000年，由waldhauser和ellsworth提出了双差定位法，与主事件相对定位法不同，事件对的距离不受限制，大大提高了方法的适用性。在反演方法上逐渐引入非线性定位方法，如牛顿法、全局搜索方法，powell法、遗传算法、模拟退火算法等。几何作图法具有稳健、效率高的优势，但定位精度低；线性定位法无需速度模型精度，但对初至拾取的精度有较高要求；非线性定位法对初至拾取较为敏感，对速度模型的精度要求较高，但计算量较小。


技术实现要素：

3.本发明提供一种基于假想源的二次定位计算的微地震定位方法，能够精准定位微地震事件源。
4.本发明的技术方案是：一种基于假想源的二次定位计算的微地震定位方法，首先设定一系列的“假想源”，读取检波器数据，模型数据，微地震事件走时数据，根据地震的互易性原理，计算各个检波器作为源到“假想源”的走时，把上述走时数据作为对比数据集，以实际观察走时数据与数据集进行对比匹配，计算每一个地震事件满足条件的射线数和残差和，迅速确定微地源事件发生的微区域和参考“假想源”，然后再在微区域内以参考“假想源”为基点，采用最小二乘法二次精准定位微地震事件位置，其步骤具体包括：
5.步骤1，利用地震的互易性原理，计算时间场值，对观察到的走时数据进行匹配，迅速定位地震发生的小分块和“假想源”，初次匹配确定地震发生域；
6.1.1、建立分块-节点模型
7.首先读取检波器数据、模型数据、地震信息，对地质模型采用分块-节点法进行数字化，利用不同灰度块或不同颜色代表不同速度的介质，然后在不同速度块利用节点对模型进行细分，并且节点间距不固定，是可变的，利用复杂模型的数字化读取模型信息；采用井中、井地结合、井间多种方法布设检波器进行微地震信号采集，读取地震信息，即地震事件实际走时；在建立的模型内读取检波器的水平坐标和深度坐标数据；
8.1.2、自动加密模型获取小分块中点
9.以1.1中建立的模型的原有纵横坐标节点为依据，在纵横坐标相邻节点的中点设置多个加密点进行加密，各加密点形成的矩形小分块，将小分块中点进行标记作为“假想源”；
10.1.3、利用互易性计算时间场
11.利用互易性把检波器作为“震源”，利用射线追踪方法计算从检波器传出来的波到“假想源”的走时场，每个检波器形成1个走时场数据集；
12.1.4、匹配对比确定微震发生域
13.将每个检波器中观察的地震事件的实际走时与1.3中获得的走时场数据集进行对比，数据相同时计射线数为1，统计射线数，统计射线数时应该满足以下条件：
[0014][0015]
其中t
实
为检波实际观察到的走时数据，t
假
为假想源的走时，即1.3所得到假想源时间场值，d
x
为模型中两个圆形的原始网格节点水平方向的间距，dh为模型中两个圆形的原始网格节点深度方向的间距，v
分
为以小分块中点为中心，以圆点为角点的小分块内波传播速度；
[0016]
当实际震源离假想源较远，在小分块边源时，有可能统计的射线数在两个小分块相同，均为统计的射线数的最大值，此时不利用第二步的二次定位，为了避免此时无法初始匹域震源所在小分块，计匹配射线时数，同时统计走时残差和，其计算公式如下：
[0017][0018]
其中t
和
代表残差和，t
实
和t
假
分别代表微地震事件实际观察走时和1.3中理论计算假想源的走时，i代表检波器序号，n代表总检波器数量；
[0019]
射线数最大，残差和最小位置即为初步匹配的假想源位置，该假想源所在的小分块即为微震事件发生的可能区域；
[0020]
步骤2，利用假想源进行二次定位，准确确定震源位置；
[0021]
2.1、二次参考事件精准确定震源位置
[0022]
二次定位是相对定位方法，根据如下计算公式：
[0023][0024]
其中t
实
为实际观察到的走时，t
假
为假想源的走时，δx
l
为坐标扰动量，为时间场对坐标导数，δτ为时间扰动量，l代表不同坐标轴，l为2时为二维情况，l为3时为三维情况。
[0025]
2.2、计算上述公式(3)中的导数值
[0026]
确定实际走时的时间场对坐标的导数值，利用模型中的原始网格节点，加密点，小
分块中点的走时数据，建立时间场与坐标系的二次趋势面方程：
[0027]
ti＝a0+a1x+a2h+a3x2+a4xh+a5h2ꢀꢀꢀ
(4)
[0028]
其中ti为实际走时，即从检波器到节点处的走时，i代表节点的序号，x代表水平坐标，h代表深度坐标，a0、a1、a2、a3、a4、a5分别是系数；
[0029]
将数据代入(4)式采用最小二乘法计算获得系数，同时可得对x，对h的导数值：
[0030][0031][0032]
最终代入公式(3)二次精准定位震源位置。
[0033]
本发明的优点是：
[0034]
1)本发明利用地震互易性，一次计算完所有“假想源”的走时场，避免了反复射线追踪过程的时间损耗，能够精准定位微地震事件源；
[0035]
2)本发明利用射线数和走时残差和，快速匹配锁定震源区，避免了扫描法或非线性方法反复调整源区的过程，节省了大量计算损耗；
[0036]
3)本发明利用参考“假想源”在小分块中进行二次定位，是相对定位方法，避免了模型速度依赖，且计算量很小；
[0037]
4)本发明在小分块中二次定位计算时，采用趋势面拟合方法，很好的解决了小范围内时间场导数的求取问题；
[0038]
5)本发明不仅可适用的二维情况，同时可扩展到三维情况，将由二维的矩形域扩展成三维情况的矩形体。
附图说明
[0039]
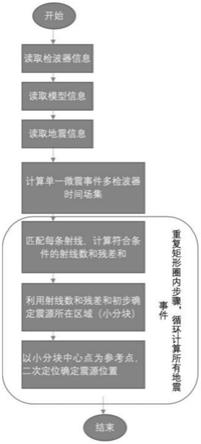
图1是本发明流程示意图；
[0040]
图2是本发明地质模型采用分块-节点法进行数字化后的示意图；
[0041]
图3是本发明读取地震信息时的示意图，a为单井采集模式，b为井地结合采集模式，c为双井采集模式；
[0042]
图4是本发明自动加密后的模型示意图；
[0043]
图5是本发明利用互易性计算各检波器为源的时间场的数据集；
[0044]
图6是本发明二次定位原理示意图；
[0045]
图7是本发明实施例1各向同性均匀介质中定位测试中数据模型化结果和检波器位置分布示意图；
[0046]
图8是本发明实施例1各向同性均匀介质中定位测试中走时场图；
[0047]
图9是本发明实施例1各向同性均匀介质中定位测试中两个地震事件射线数与小分块残差和结果图；
[0048]
图10是本发明实施例1各向同性均匀介质中定位测试中定位结果图；
[0049]
图11是本发明实施例2层状介质中的测试中模型化结果及检波器分布示意图；
[0050]
图12是本发明实施例2层状介质中的测试中走时场图；
[0051]
图13是本发明实施例2层状介质中的测试中两个地震事件射线数与小分块残差和
结果图；
[0052]
图14是本发明实施例2层状介质中的测试中定位结果图；
具体实施方式
[0053]
下面结合附图对本发明做清楚完整的描述，以使本领域的技术人员在不需要作出创造性劳动的条件下，能够充分实施本发明。
[0054]
如图1所示，一种基于假想源的二次定位计算的微地震定位方法，利用“假想源”分两步进行精准定位震源位置，其步骤包括：
[0055]
步骤1，利用地震的互易性原理，计算时间场值，对观察到的走时数据进行匹配，迅速定位地震发生的小分块和“假想源”，初次匹配确定地震发生域；
[0056]
步骤2，利用假想源进行二次定位，准确确定震源位置。
[0057]
上述步骤1具体包括：
[0058]
1.1、建立分块-节点模型
[0059]
首先读取检波器数据、模型数据、地震信息(即微地震事件走时)，如表1-3所示，对地质模型采用分块-节点法进行数字化，如图2所示，不同灰度块代表不同速度的介质，然后在不同速度块利用节点(图2中x符号)，对模型进行细分，并且节点间距不固定，是可变的，利用复杂模型的数字化读取模型信息，如表2所示；
[0060]
在建立的模型内读取检波器的水平坐标和深度坐标数据，如表1所示；
[0061]
读取地震信息，采用井中、井地结合、井间多种方法布设检波器进行微地震信号采集，读取地震信息，如图3所示，信息数据如表3所示；
[0062]
表1检波器数据
[0063]
检波器编号水平坐标深度坐标1x1h12x2h2
………
[0064]
表2模型数据格式
[0065]
节点编号水平坐标深度坐标速度值1x1h
1v1
2x1h
2v2
…………
nx1h
nvn
n+1x2h
1vn+1
n+2x2h
2vn+2
…………
n+nx2h
nvn+n
…………
(m-1)*n+1x
mh1v(m-1)*n+1
(m-1)*n+2x
mh2v(m-1)*n+2
…………
m*nx
mhnvm*n
[0066]
表3地震信息数据格式
[0067][0068]
1.2、自动加密模型获取小分块中点
[0069]
以图2中原有纵横坐标节点为依据，在纵横坐标相邻节点的中点设置多个加密点，自动加密结果如图4，图4中五星代表检波器位置，圆点是图2中原始网格节点位置，三角形是加密之后的小分块中点，即假想源位置，x位置是加密点。
[0070]
1.3、利用互易性计算时间场
[0071]
从震源发出来的波到检波器的走时与从检波器发出的波到震源的走时是相同的，正是利用此地震互易性原理，在不知道真实震源位置的情况下，把检波器作为“震源”，利用射线追踪方法计算从检波器传出来的波到“假想源”，即小分块中点的走时场，如图5所示是图4中六个检波器作为源的走时场，每个检波器形成1个走时场数据集。
[0072]
1.4、匹配对比确定微震发生域
[0073]
假设某一个“假想源”是真实的震源位置，那震源到6个检波器的6条射线走时，必然分别在图5中的6个数据集中，第一个检波器中观察的实际走时，与数据集1进行对比，震源位置的走时数据与实际走时相同，此时计射线数为1，同样对比第二、三、四、五、六检波器的实际走时与走时数据集，统计其射线数，实际震源位置射线数必然为6，把震源限定在图4中以三角形为中心，以圆点为角点的小分块内，此时统计射线数时应该满足以下条件：
[0074][0075]
其中t实为检波实际观察到的走时数据，t假为假想源的走时，即1.3计算所得到假想源时间场值，d
x
为图4中两个原始网格节点水平方向的间距，dh为图4中两个原始网格节点深度方向的间距，v
分
为以三角形为中心，以圆点为角点的小分块内波传播速度。
[0076]
当实际震源离假想源较远，在小分块边源时，有可能统计的射线数在两个小分块相同，均为统计的射线数的最大值，此时不利于第二步的二次定位，为了避免此时无法初始匹配震源所在小分块，统计匹配射线数时，同时统计走时残差和，其计算公式如下：
[0077][0078]
其中t
和
代表残差和，t
实
和t
假
分别代表微地震事件实际观察走时和理论计算假想源
的走时，i代表检波器序号，n代表总检波器数量。
[0079]
通过公式(1)和公式(2)计算的射线数和残差和如表4和表5，易知射线数最大，残差和最小位置即为初步匹配的假想源位置，该假想源所在的小分块即为微震事件发生的可能区域。
[0080]
表4各分块符合条件的射线数
[0081][0082][0083]
表5各小分块射线残差和
[0084][0085]
2.1、二次参考事件精准确定震源位置
[0086]
二次定位是相对定位方法，如图6所示，三角形是小分块中点，为假想地震源，实际震源位置在圆点网格点所围小分块内一点，根据如下计算公式：
[0087]
[0088]
其中t
实
为实际观察到的走时，t
假
为假想源的走时，δx
l
为坐标扰动量，为时间场对坐标导数，δτ为时间扰动量，l代表不同坐标轴，l为2时为二维情况，l为3时为三维情况。
[0089]
2.2、计算上述公式(3)中的导数值
[0090]
确定实际走时的时间场对坐标的导数值，利用图6中原始网格节点，加密点，小分块中点共9个点的走时数据，建立时间场与坐标系的二次趋势面方程：
[0091]
ti＝a0+a1x+a2h+a3x2+a4xh+a5h2ꢀꢀꢀ
(4)
[0092]
其中ti为实际走时，即从检波器到节点处的走时，i代表节点的序号，i最大为9，x代表水平坐标，h代表深度坐标，因此把9个点的走时数据全部代入方程(4)变为9个方程的方程组，此时需要确定(4)式的系数，此方程的求解同样采用最小二乘法，获得系数后，可得对x，对h的导数值：
[0093][0094][0095]
最终代入公式(3)二次精准定位震源位置。
[0096]
实施例1：各向同性均匀介质中定位测试
[0097]
数据模型化结果和检波器位置如图7，设置2个地震事件6个检波器的接收的走时数据，如表6所示。
[0098]
表6均匀介质中走时数据
[0099][0100]
根据预设的到时数据与波场走时正演结果值，可以确定两个震源范围位于图7中的矩形区域框内。
[0101]
读取检波器、模型数据、地震信息后，根据互易性，计算检波器作为震源的走时图，如图8所示，按图4中的方式进行网格加密，匹配表6的走时与图8中小分块中心的走时值，进行满足条件射线数与小分块残差和计算，两个地震结果如图9所示。
[0102]
依据图9中的射线数最大值和残差和最小值，确定的小分块中心如图10所示，然后
进行二次参考事件定位，其定位结果如图10所示。
[0103]
实施例2：层状介质中的测试，选择了井地联合的检波器布设方式，其模型化结果及检波器分布图11，地震事件数据如表7所示，其震源位置应落在图11的矩形框内。
[0104]
表7层状介质微地震走时数据
[0105][0106]
读取检波器、模型数据、地震信息后，根据互易性，计算检波器作为震源的走时图如图12所示。
[0107]
按图4中的方式进行网格加密，匹配表7的走时与图12中小分块中心的走时值，进行满足条件射线数与小分块残差和计算，两个地震结果如图13所示，a为射线数，b为残差和。
[0108]
依据图13中的射线数最大值和残差和最小值，确定的小分块中心如图14所示，然后进行二次参考事件定位，其定位结果如图14所示。
[0109]
以上对本发明的较佳实施例进行了描述，需要指出的是，本发明，并不局限于上述特定实施方式，其中未尽详细描述的设备和结构应该理解为用本领域中的普通方式予以实施；任何熟悉本领域的技术人员，在不脱离本发明技术方案范围情况下，依据本发明的技术实质对以上实施例所做的任何简单修改、等同变化及修饰，均仍属于本发明技术方案保护的范围内。