一种共激发点动校正实现方法

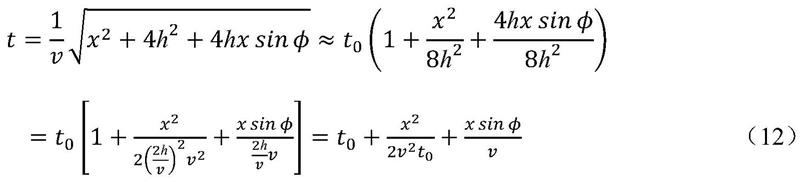
1.本发明属于地震勘探技术领域，具体涉及一种共激发点动校正实现方法。


背景技术：

2.地震反射波勘探理论的教学过程中和实际应用过程中，正常时差(也叫动校正量)和动校正的理论和技术都是其它理论和技术无法替代的。然而，现行权威的地震勘探文献中对正常时差(动校正量)的定义如下(陆基孟,王永刚，2011)：在界面水平情况下，对界面上某点以炮检距x进行观测得到的反射波旅行时与以零炮检距(自激自收)进行观测得到的反射波旅行时之差；现在地震勘探文献对动校正的定义为(陆基孟,王永刚，2011)：在水平界面情况下，从观测到的反射波旅行时中减去正常时差(动校正量)，得到相当于炮检距中点处的自激自收时间。可见，目前文献对正常时差(动校正量)和动校正的定义都局限于水平反射面的情况下，但地震勘探的目的是倾斜的反射面，所以需要明确倾斜反射面情况下的正常时差(动校正量)和动校正的定义。另外还有文献对正常时差(动校正量)和动校正的概念没有给出明确的定义。
3.定义正常时差(动校正量)的概念是为动校正服务的。从上述正常时差(动校正量)定义和动校正定义可以看出，其正常时差(动校正量)定义和动校正定义存在矛盾。具体矛盾解释如下，把正常时差(动校正量)用公式表示为：
4.正常时差(动校正量)＝地震波旅行时
‑
激发点的自激自收时间
5.动校正定义用公式表示为：
6.炮检距中点的自激自收时间＝地震波旅行时
‑
正常时差
7.如果联立上述两个公式，就会得到激发点的自激自收时间＝炮检距中点的自激自收时间，这应该仅仅适用于水平反射面。为了使正常时差(动校正量)和动校正的定义适用于倾斜反射面，我们认为正常时差(动校正量)应该定义为：在倾斜反射面条件下，反射波旅行时与炮检距中点的自激自收时间之差。
8.目前动校正的具体计算过程还存在另外两点不足，一是没有说明共激发点动校正与共中心点动校正区别，也就没有阐述用两种动校正确定反射点法线深度的明确步骤；二是没有对动校正勘探的实现和检验过程。然而，对动校正勘探结果的实现和检验，无论对地震勘探的实践，还是对地震勘探的理论或教学，都具有深刻的理论和实践价值。
9.参考文献：陆基孟,王永刚.地震勘探原理[m].第三版,山东东营:中国石油大学出版社,2011,第35页.


技术实现要素：

[0010]
针对目前地震勘探教材对正常时差(动校正量)和动校正的定义都局限于水平反射面的情况，给出正常时差(动校正量)定义是：在反射界面倾角较小(在地球物理勘探中，一般认为斜面倾角较小为小于15
°
)条件下，正常时差(动校正量)是反射地震波旅行时减去炮检距中点对应的自激自收时间。把动校正定义为：在反射角面倾角较小(小于15
°
)的条件
下，反射波旅行时减去正常时差(动校正量)，得到炮检距中点处的自激自收时间。
[0011]
下面对正常时差(动校正量)和动校正的定义展开说明。
[0012]
为便于理解，按着目前教材的习惯，首先把水平反射面正常时差(动校正量)定义为反射地震波旅行时减去反射点对应的自激自收时间，于是：
[0013]
δt＝t
‑
t
0r
(1)
[0014]
公式(1)中δt为正常时差(动校正量)；t为地震波旅行时；t
0r
为反射点的自激自收时间，注意我们这里定义的不是炮检距中点的自激自收时间。这样定义的目的是，如果能够计算得到正常时差(动校正量)δt，就可以根据公式(1)得到反射点的自激自收时间t
0r
，进一步根据公式(2)计算反射点法线深度。
[0015][0016]
公式(2)中h
r
为反射点法线深度；v为地震波传播速度。
[0017]
如图1，o点为地震波激发点，s为地震波接收点，x为炮检距，m点为炮检距中点，反射面ab的深度为h，也是激发点的深度，反射面以上介质的波速为v，假定ab为水平反射面，所以炮检距中点m的正下方就是反射点。我们现在把水平反射面正常时差(动校正量)定义为反射地震波旅行时减去检波距中点对应的自激自收时间，用公式表示：
[0018]
δt
h
＝t
‑
t
0m
(3)
[0019]
公式(3)中，δt
h
为水平反射面下的正常时差(动校正量)，以便区别于以后的倾斜反射面。t
0m
是炮检距中点对应的自激自收时间，对于水平反射面也是反射点的自激自收时间。所以，在水平反射面正常时差(动校正量)可以定义为反射地震波旅行时减去检波距中点对应的自激自收时间，这样定义不会影响反射点法线深度的计算。
[0020]
下面，计算水平反射面下的动校正量。
[0021][0022]
公式(4)中为反射波旅行时，h
m
为炮检距中点对应的法线深度，h为激发点法线深度，对于水平反射面h
m
＝h，地震反射波旅行时可以如下表示：
[0023][0024]
公式(5)中为激发点自激自收时间，对水平反射面t0＝t
0m
。当x/2h＜＜1时，就是假定勘探深度远远大于炮检距的情况下，用泰勒级数展开得到简单的近似公式：
[0025][0026]
略去高阶无穷小，得到：
[0027][0028]
可以用公式(7)中计算动校正量，其中的t0为激发点的自激自收时间。
有了动校正量，把公式(7)变形，得到公式(8)计算炮检距中点的自激自收时间。
[0029]
t
0m
＝t
‑
δt
h
(8)
[0030]
有了炮检距中点的自激自收时间，就可以根据公式(9)计算炮检距中点的对应的法线深度h
m
。对于水平反射面，也就是反射点的法线深度。
[0031][0032]
要确定法线深度理论上需要掌握反射点位置。对于水平反射面，反射点对应在炮检距的中点处，但对于倾斜反射面，反射点一定不对应在炮检距中点，如图2，并且斜面倾角越大，反射点越偏离炮检距中点。当反射面倾角足够大时，反射点会出现在激发点与接收点连线之外。由于反射面未知，所以反射点的位置也不能确定，反射点位置未知，准确确定反射点法线深度在理论上是不可能的；反过来说，如果已知反射点位置，确定反射点法线深度也就简单了。为了能够确定反射点法线深度，物探中规定作为勘探对象的反射面倾角比较小，此时的反射点近似对应在炮检距的中点上。图2中的反射面倾角比较大，真正的反射点r与炮检距中点对应的反射点r’距离较远，但如果反射面倾角减小，两个点就接近了。也就是反射面的倾角很小时，反射点与炮检距中点就基本重合，也就是在目前地球物理勘探中，假定反射面的倾角很小，就可以把炮检距中点近似定义为反射点了。现在就可以得到本节开始时正常时差(动校正量)和动校正的定义了。
[0033]
所以在反射面倾斜条件下，定义动校正量依然定义为地震波旅行时减去炮检距中点m处的自激自收时间t
0m
(相当于反射点的自激自收时间)，用δt
φ
表示倾斜反射面的动校正量，区别于水平反射面上的动校正量δt
h
。
[0034][0035][0036]
公式(10)中的t为图2中下行波的旅行时，进一步简化旅行时：
[0037][0038]
公式(12)中为激发点的自激自收时间。
[0039]
从图2可以看出：
[0040][0041][0042]
比较公式(7)中的水平反射面的动校正量δt
h
和公式(14)中的倾斜反射面动校正量δt
φ
，发现两者近似相等，所以，虽然我们不知道反射面情况，但我们可以用计算水平反射面动校正量的方法计算倾斜反射面的动校正量。也正因为如此，我们可以用δt
φ
表示任
意反射面倾角下的动校正量。并且在反射面倾角较小的假定下，反射点对应在炮检距中点，从而用公式(15)计算出该共中心点自激自收时间(t
0m
)，并用公式(9)确定该点法线深度。
[0043]
t
0m
＝t
‑
δt
φ
(15)
[0044][0045]
动校正量的公式(14)中h为激发点法线深度。在地震勘探中，往往需要通过钻孔等方法确定勘探的目标层在该点的深度，进一步用地震勘探方法确定该目标层法线深度。
[0046]
一种共激发点动校正实现方法，并确定反射面，其实施方式流程图如图3所示。具体流程如下：
[0047]
步骤1：建立纵测线，确定激发点和接收点的位置坐标x，掌握反射层以上介质的地震波速度v，目标层在激发点处的法线深度h，并用公式(16)计算激发点的自激自收时间t0；
[0048][0049]
步骤2：激发地震波，在接收点记录地震波旅行时t；
[0050]
步骤3：用公式(14)计算动校正量(δt
φ
)；
[0051][0052]
步骤4：用公式(15)计算炮检距中点对应的自激自收时间(t
0m
)；
[0053]
t
0m
＝t
‑
δt
φ
又(15)
[0054]
步骤5：用公式(9)计算法线深度(h
m
)；
[0055][0056]
步骤6：用偏移归位法确定反射面(陆基孟，王永刚，2011，210页)。
[0057]
有益技术效果：
[0058]
本发明属于地震勘探技术领域，具体涉及一种共激发点动校正实现方法。目前文献对正常时差(动校正量)和动校正的定义都局限于水平反射面的情况下，但地震勘探的目的是倾斜反射面，所以需要明确倾斜反射面情况下的正常时差(动校正量)和动校正的定义。本发明在倾斜反射面条件下，准确定义了正常时差(动校正量)和动校正的概念，并提出共激发点动校正的概念，首次明确了用共激发点勘探的前提是在地震波速度和目标层在激发点的法线深度已知条件下；首次明确了共激发点动校正确定反射面的步骤，方便操作；首次具体实现了用共激发点动校正勘探反射面；首次把理论时距曲线数据作为地震记录，以检验地震勘探理论。这无论对地震勘探的实践，还是对地震勘探的理论或教学，都具有理论和实践价值。
附图说明
[0059]
图1为本发明实施例的水平反射面示意图；
[0060]
图2为本发明实施例的倾斜反射面示意图；
[0061]
图3为本发明实施例的流程图；
[0062]
图4为本发明获取地震记录用的反射面；
[0063]
图5为本发明反射面倾角为5
°
时的勘探结果与实际反射面的比较；
[0064]
图6为本发明反射面倾角为1
′
时的勘探结果与实际反射面的比较；
[0065]
图7为本发明反射面倾角为2
°
时的勘探结果与实际反射面的比较；
[0066]
图8为本发明反射面倾角为10
′
时的勘探结果与实际反射面的比较。
具体实施方式
[0067]
下面结合附图和具体实施实例对发明做进一步说明，说明一种共激发点动校正实现方法的步骤，一种共激发点动校正实现方法，具体流程如下：
[0068]
步骤1：建立纵测线，确定激发点和接收点的位置坐标x，掌握反射层以上介质的地震波速度v，目标层在激发点处的法线深度h，并用公式(16)计算激发点的自激自收时间；
[0069][0070]
本次探测的激发点的法线深度h＝300m，波速v＝400m/s，自激自收时间t0＝1.5s；
[0071]
步骤2：激发地震波，在接收点记录地震波旅行时t；
[0072]
在自然界中找到一个已知的反射面几乎是不可能的。为了得到地震波走时准确数据，通过理论模型获得数据是必要的。假定如图4的倾斜反射面r，通过理论计算可以得到地震波走时随位置坐标的变化关系。图4中反射面倾角φ＝5
°
，以o点为激发点，od之间距离取300m，从o到d点每隔10m取一个接收点作为记录点，o点的法线深度h＝300m，v＝400m/s，得到图4中的上行波记录，在本次验证中仅仅用上行波数据；
[0073]
获得图4中反射波走时的计算方程为公式(17)。取反射面倾角φ为5
°
得到地震波走时数据，见表1中第一列和第二列；
[0074][0075]
表1勘探数据
[0076][0077]
步骤3：用公式(14)计算动校正量，见表1中第一列和第三列；
[0078][0079]
步骤4：用公式(15)计算炮检距中点对应的自激自收时间，见表1中第一列和第四列；
[0080]
t
0m
＝t
‑
δt
φ
又(15)
[0081]
步骤5：用公式(9)计算法线深度，见表1中第一列和第五列；
[0082][0083]
步骤6：用偏移归位法确定反射面(陆基孟，王永刚，2011，210页)，如图5中细线是当反射面倾角为5
°
时用共激发点勘探得到的勘探结果，粗线是设定的反射面；分别取反射面倾角φ为1
°
、2
°
、10
°
，重复上述步骤，所得勘探结果分别如图6至图8所示。其中图6中细线是当反射面倾角为1
°
时用共激发点勘探得到的勘探结果，粗线是设定的反射面；图7中细线是当反射面倾角为2
°
时用共激发点勘探得到的勘探结果，粗线是设定的反射面；图8中细线是当反射面倾角为10
°
时用共激发点勘探得到的勘探结果，粗线是设定的反射面。可以看出，实际反射面与用共激发点动校正计算得到的反射面都有一个交点，该位置恰好在激发点处，该点计算结果与反射面实际位置吻合。总体来说实际反射面与用共激发点动校正计算得到的反射面差异比较大，并且勘探点离激发点越远，两者差异越大；反射面倾角越大，
勘探结果与实际的反射面差异越大，表明计算结果有较大误差。但计算结果正确地反映了勘探面相对深度，在一定程度上解决了地震勘探问题，该方法有一定的实用价值。