一种基于直升机平台的SAR振动误差估计及补偿方法与流程

一种基于直升机平台的sar振动误差估计及补偿方法
技术领域
1.本发明属于sar成像技术领域，具体涉及一种基于直升机平台的sar振动误差估计及补偿方法。


背景技术：

2.合成孔径雷达(sar)成像技术是通过平台运动形成虚拟大孔径实现方位高分辨，从而获得观测场景的高分辨遥感图像。平台运动既是成像的根本，也是影响成像质量的主要问题之一。为了形成理想均匀直线阵列，要求平台运动矢量在合成孔径时间内保持不变。但在机载sar成像处理中，大气扰动及平台巡航精度等因素将导致天线相位中心的位置偏移误差，所引入的运动误差将导致成像的散焦和几何形变，对机载高分辨成像，运动补偿必不可少。
3.对于传统的固定翼飞机及各型无人机，利用载机惯性导航系统(ins)和全球定位系统(gps)同步记录的平台位置和运动信息实现机载运动补偿是现有机载sar成像处理中应用最为广泛的处理手段，现代高精度导航系统精度可达到厘米级，能有效补偿回波数据中大部分运动误差，对于剩余运动误差，可以采用基于数据自聚焦处理技术，如相位梯度自聚焦(pga)、子孔径偏置(md)等算法进行估计补偿。经过惯导+数据的两步补偿处理，sar回波信号中的绝大部分运动误差能够得到有效估计及补偿，再结合相应的成像处理算法，即可获得高分辨sar图像结果。
4.相较于固定翼飞机平台，直升机平台成像过程中，不仅会受到大气扰动的影响，同时平台自身存在的高频振动也会叠加在接收到的回波信号之中，导致回波中不仅存在平台运动偏离带来的低频运动误差，还存在有平台振动带来的高频误差。传统的惯导+自聚焦两步运动误差补偿算法仅对低频误差具有较好的处理效果，无法对存在的高频振动误差进行精确的估计补偿，进而导致散射点旁瓣水平抬高，分辨率下降，整体图像质量恶化。如何精确地估计补偿信号中存在的高频振动误差，是获取直升机平台下聚焦效果良好的高分辨sar图像的关键。


技术实现要素：

5.要解决的技术问题
6.理想的机载sar成像期望平台运动矢量需要在合成孔径时间内保持不变，但对直升机载平台而言，受气流、振动等因素的影响，天线相位中心的位置会产生较为明显的偏移运动误差。不同频率成份的运动误差对sar成像的影响也不尽相同，其中低频振动主要造成二次相位畸变，图像方位分辨率下降；高频振动主要造成旁瓣电平升高、强目标点会出现周期性的重影、积分旁瓣抬高等现象，因此为实现直升机载高分辨sar成像，需要进行较为精确的运动补偿处理。
7.利用载机惯性导航系统(inertial navigation system,ins)和全球定位系统(global position system,gps)组成的组合导航系统同步记录平台位置和运动信息可以
实现直升机机载sar成像的运动补偿，也是目前最常用、最为可靠的手段。但受限于惯导数据率、精度等影响，组合导航系统往往无法准确测量出载机平台运动误差，必将导致rd类成像算法前期的运动补偿存在残余运动误差。此时经方位fft变换后，回波多普勒谱通常会存在一定的偏移和扭曲，从而造成基于多普勒域解耦和处理的距离徙动校正精度急剧下降。
8.技术方案
9.一种基于直升机平台的sar振动误差补偿成像方法，其特征在于步骤如下：
10.步骤1：建立含振动误差斜距模型；
11.假设sar发射信号的脉冲重复周期为tr，则天线相位中心相邻慢时间理想间距为vtr，理想高度为h，天线相位中心在慢时间t的瞬时真实和理想位置坐标分别表示为[vt+δx(t),δy(t),h+δz(t)]和[vt,0,h]，瞬时运动误差矢量定义为d＝[δx(t),δy(t),δz(t)]，其中δy(t)和δz(t)分别表示载机平台在y轴和z轴方向上的瞬时位置偏差；假设雷达正侧视工作，即雷达斜视角α＝0，地面某散射点坐标为(x,y,z)，则其到天线相位中心的瞬时斜距表示为：
[0012][0013][0014][0015]
其中，表示目标到理想航线的最短距离，和cosθ＝h/r，θ表示雷达视线入射角；式(1)中真实斜距分解成两项：r0表示理想斜距表达，δr表示为斜距误差；斜距误差表达式(3)中的第一项表示沿航向运动误差，第二和第三项表示垂直航向运动误差；基于窄波束和场景为平地的假设，运动误差的空变性可近似为仅随距离空变，式(3)近似为：
[0016][0017]
步骤2：利用斜距模式构建回波信号，对其进行相干检波与距离脉压处理，并变换至距离频域-方位时域；
[0018]
sar系统发射线性调频信号，即有
[0019][0020]
其中，τ为快时间，fc为信号载频，t
p
为发射信号脉宽，γ为调频率；经过相干检波，接收回波信号表示为：
[0021][0022]
其中，r和x分别为距离和方位坐标，c为光速，σ(r,x)对应目标的复散射系数，g(t)表示天线方向图以及其他方位时变特征；通过傅立叶变换将上式变换到距离频率域表达为：
[0023][0024]
其中，s
t
(fr)＝ft[s
t
(τ)]，ft[
·
]表示傅里叶变换操作；
[0025]
步骤3：子孔径划分及走动校正处理；
[0026]
将距离脉压后的回波数据沿方位维将其分为n个子孔径，每个子孔径长度为m，其中子孔径间的重叠量为m/2，利用惯导数据构建对应子孔径下的轨迹运动误差粗补偿相位h
err_com1
(fr,ta)
[0027][0028]
其中，c为光速，fr表示距离频率，ta为方位时间，r
ref
(ta)表示对应方位时刻ta的瞬时斜距，且有
[0029][0030]
其中，v表示平台速度，h为工作高度，rc表示场景中心斜距，xc与yc为根据载机运动方向建立笛卡尔坐标系下x轴与y轴的起始坐标，x
err
、y
err
与z
err
分别为根据惯导数据解算得到的x向、y向与z向的运动误差；将构建的粗补偿相位h
err_com1
(fr,ta)与信号相乘后，将信号变换回二维时域，通过对信号能量累加排序的方式筛选出强散射点样本，构建调频率项对其进行dechirp处理后沿方位向傅里叶变换，搜索方位向上能量最强点，计算出其对应的多普勒频率fd，进而可以反算得到相应的走动角θ
rmc
，即有
[0031]
θ
rmc
＝asin(fdλ/2v)
ꢀꢀꢀ
(10)
[0032]
λ表示波长，利用走动角θ
rmc
，即可构建线性走动补偿项h
lrmc
(fr，ta)
[0033][0034]
利用上式即可对脉压后的信号进行走动校正处理；
[0035]
步骤4：利用epga算法估计子孔径运动误差；
[0036]
在对子孔径数据完成走动补偿后，利用epga算法对子孔径数据进行运动误差估计，包括样本选择、循环移位、加窗滤波、相位梯度估计、迭代相位估计和相位补偿；
[0037]
步骤5：将子孔径误差拼接后获得全孔径误差，进而对数据进行补偿，消除运动误
差的影响；
[0038]
假设采用epga自聚焦算法提取的每个子孔径回波数据的相位误差矢量为：
[0039]
ωn＝[ω
n,1
,ω
n,2
,
…
,ω
n,m
,
…
,ω
n,m
],n＝1,2,
…
,n；m＝1,2,
…
,m；
[0040]
其中，n表示第n个子孔径，m表示从某个子孔径中第m个脉冲回波数据提取出的相位误差；令ωn＝[ω
n,1
,ω
n,2
,
…
,ω
n,m
]、ω
n+1
＝[ω
n+1,1
,ω
n+1,2
,
…
,ω
n+1,m
]分别表示由第n个和第n+1个子孔径回波数据估计得到的相位误差矢量，其中ω
′n＝[ω
n,m/2+1
,
…
,ω
n,m
]、ωn+1＝[ω
n+1,1
,
…
,ω
n+1,m/2
]为两个子孔径间相位误差矢量的重叠部分，利用线性表达式：y＝kx+b，其中y＝ω
′
n-ω
′
n+1
，x
…
1,2,
…
,m/2，通过线性拟合的方式得到拟合系数k和b；
[0041]
利用拟合到的线性拟合系数k和b，对第n+1个子孔径的相位误差矢量进行修正，使之与第n个子孔径的相位误差矢量保持线性连续，则修正后的第n+1个子孔径相位误差矢量为：其中n从1开始，并将修正后的第n+1个子孔径相位误差矢量与第n+2个子孔径相位误差矢量ω
n+2
重复之前的拟合步骤，直到n个子孔径相位误差矢量全部修正完毕；
[0042]
将第1个子孔径的相位误差矢量ω1与修正后(n-1)个子孔径相位误差矢量的后半段进行拼接，得到全孔径的相位误差矢量ω，其长度为m+(n-1)m/2＝(n+1)m/2，对相位误差矢量ω进行高通滤波，假设滤波器系数为γ，高通滤波后的高频相位误差矢量为其中表示卷积操作；利用全孔径相位误差矢量对回波数据进行相位补偿，即可实现运动误差的消除，最终获取聚焦良好的高分辨sar图像。
[0043]
一种计算机系统，其特征在于包括：一个或多个处理器，计算机可读存储介质，用于存储一个或多个程序，其中，当所述一个或多个程序被所述一个或多个处理器执行时，使得所述一个或多个处理器实现上述的方法。
[0044]
一种计算机可读存储介质，其特征在于存储有计算机可执行指令，所述指令在被执行时用于实现上述的方法。
[0045]
一种计算机程序，其特征在于包括计算机可执行指令，所述指令在被执行时用于实现上述的方法。
[0046]
有益效果
[0047]
本发明主要针对直升机载平台合成孔径雷达进行观测成像时存在的直升机平台自身振动引起的图像聚焦质量下降问题，通过分析回波信号以及振动误差特性，建立相应的含误差信号回波模型，并在此基础上，结合相位梯度自聚焦算法的处理思想，设计完整的运动误差估计及补偿处理流程，消除高频振动误差对成像聚焦的影响，进而获取聚焦效果良好的高分辨sar图像。
[0048]
与现有技术相比，采用本发明方法对直升机载合成孔径雷达成像中存在的振动误差进行估计补偿时，具有如下有益效果：
[0049]
传统运动误差补偿处理往往会忽略距离校正精度的影响，仅在方位脉压后的sar图像域采用相位梯度自聚焦算法进行补偿，但此时高频运动误差对距离多普勒域解耦合的影响已经产生，后续的运动误差估计与补偿效果明显下降。此外，振动误差分量较为复杂，直接进行拟合补偿精度较差。本发明将惯导粗补偿与距离走动补偿处理相结合，在估计振动误差之前对回波进行预处理，再结合稳健的加权相位梯度自聚焦算法估计出误差中的低
频分量并将其从误差中去除，并对剩余的误差进行高通滤波进一步降低残余低频误差分量的影响，将滤波后的振动误差重新补偿至回波中后即可消除其对成像影响，有效改善最终的图像聚焦质量。
附图说明
[0050]
附图仅用于示出具体实施例的目的，而并不认为是对本发明的限制，在整个附图中，相同的参考符号表示相同的部件。
[0051]
图1为本发明所适用的含误差直升机载sar成像几何；
[0052]
图2为本发明误差相位线性拟合与修正示意图；
[0053]
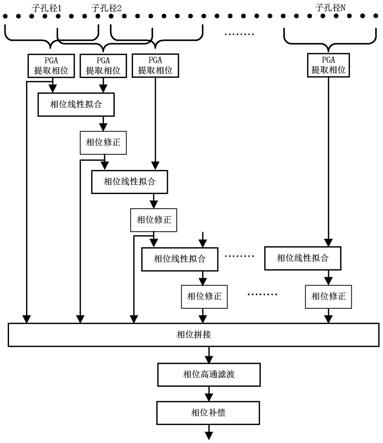
图3为本发明的流程图。
具体实施方式
[0054]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图和实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。此外，下面描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。
[0055]
本发明针对直升机载平台成像时存在的高频运动误差补偿精度较差的问题，考虑利用pga算法基于数据自适应地提取残余相位误差，并采用相位拟合、拼接和滤波等手段，有效提取回波数据中的高频相位误差分量，进而实现改善成像的目标主副瓣比和图像整体聚焦质量的目标。
[0056]
实现本发明所述的方法包括以下几步：
[0057]
(1)脉压后回波数据划分与预处理；
[0058]
(2)子孔径数据走动补偿；
[0059]
(3)epga估计高频振动误差；
[0060]
(4)全孔径误差拼接与补偿。
[0061]
其中：
[0062]
步骤(1)主要包括以下几步：
[0063]
1a)将脉压后的数据按照一定的长度进行子孔径划分，子孔径间重叠量为半个子孔径长度；
[0064]
1b)将划分后的子孔径数据距离向做傅里叶变换，变换至距离频域-方位时域；
[0065]
1c)利用惯导数据构建粗补偿相位函数h
err_com1
(fr,ta)；
[0066]
1d)将粗补偿相位h
err_com1
(fr,ta)与回波数据相乘；
[0067]
1e)将补偿后的数据做逆傅里叶变换重新变换回二维时域。
[0068]
步骤(2)主要包括以下几步：
[0069]
2a)沿距离维对信号进行累加排序，设置门限筛选出强散射点样本；
[0070]
2b)构建二次调频相位对筛选样本进行补偿，并将补偿后的信号变换至多普勒域；
[0071]
2c)再次沿方位向搜索出能量最强点，并根据其频率计算出对应多普勒频率fd和走动角度θ
rmc
；
[0072]
2d)利用走动角θ
rmc
构建线性走动补偿项h
lrmc
(fr，ta)；
[0073]
2e)利用线性走动函数h
lrmc
(fr，ta)对回波进行补偿。
[0074]
步骤(3)主要包括以下几步：
[0075]
3a)对走动补偿后数据进行加窗滤波；
[0076]
3b)计算样本不同距离单元对应的杂噪比；
[0077]
3c)将不同距离单元对应的杂噪比作为权值，利用加权相位梯度自聚焦方法估计出相应的相位梯度；
[0078]
3d)将估计得到的相位梯度进行积分获得对应的运动误差相位；
[0079]
3e)对运动误差相位进行低阶系数拟合后将其减去，即可获得剩余的高频振动误差项。
[0080]
步骤(4)主要包括以下几步：
[0081]
4a)将两个相邻子孔径估计得到高频误差的重叠部分进行线性拟合，提取相应的拟合系数；
[0082]
4b)利用获得的拟合系数，对后一个子孔径的相位误差进行修正，使其与前一个子孔径的相位误差保持线性连续；
[0083]
4c)将所有的子孔径数据按照步骤(4a)-(4b)进行修正，并将修正后相邻子孔径的误差进行拼接，最终获得全孔径相位误差；
[0084]
4d)对相位误差进行高通滤波处理；
[0085]
4e)将脉压后的回波信号变换至距离频域，并利用高通滤波后的相位误差进行补偿。
[0086]
上述步骤展开如下：
[0087]
(1)基于惯导粗补偿与走动校正的数据预处理
[0088]
直升机载sar数据录取几何模型如图1所示，图中直线表示理想航线，曲线表示平台真实飞行航线，x轴表示载机理想飞行方向。理想情况下，天线相位中心沿理想航线匀速v变化，实际中由于实际航线和理想航线存在位置偏差，天线相位中心到目标的斜距存在偏差。假设sar发射信号的脉冲重复周期为tr，则天线相位中心相邻慢时间理想间距为vtr，理想高度为h，天线相位中心在慢时间t的瞬时真实和理想位置坐标分别表示为[vt+δx(t),δy(t),h+δz(t)]和[vt,0,h]，瞬时运动误差矢量定义为d＝[δx(t),δy(t),δz(t)]，其中δy(t)和δz(t)分别表示载机平台在y轴和z轴方向上的瞬时位置偏差。假设雷达正侧视工作(α＝0)，地面某散射点坐标为(x,y,z)，则其到天线相位中心的瞬时斜距表示为：
[0089][0090][0091][0092]
其中，表示目标到理想航线的最短距离，和cosθ＝h/r，θ表示雷达视线入射角。式(1)中真实斜距分解成两项：r0表示理想斜距表达，δ
r表示为斜距误差。斜距误差表达式(3)中的第一项表示沿航向运动误差，第二和第三项表示垂直航向运动误差。基于窄波束和场景为平地的假设，运动误差的空变性可近似为仅随距离空变，式(3)近似为：
[0093][0094]
假设sar系统发射线性调频信号，即有
[0095][0096]
其中，τ为快时间，fc为信号载频，t
p
为发射信号脉宽，γ为调频率。经过相干检波，接收回波信号表示为：
[0097][0098]
其中，r和x分别为距离和方位坐标，c为光速，σ(r,x)对应目标的复散射系数，g(t)表示天线方向图以及其他方位时变特征。通过傅立叶变换将上式变换到距离频率域表达为：
[0099][0100]
其中，s
t
(fr)＝ft[s
t
(τ)]，ft[
·
]表示傅里叶变换操作。sar成像处理中,如距离多普勒算法，线性调频变标算法以及频率变标算法，首先进行距离单元徙动校正，并进行距离脉压处理，然后方位匹配滤波实现方位脉压。这些成像算法校正的rcm是针对理想航线对应雷达到目标确定的距离变化，没有考虑由于运动误差引入的包络偏移，而且由于运动误差引入的多普勒调制将导致回波多普勒谱较理想条件下多普勒谱存在偏移和畸变，甚至影响多普勒域处理算法对的校正，这在大斜视sar成像处理中尤为明显。
[0101]
因此在对回波进行距离脉压后，将脉压后的回波进行子孔径划分，利用惯导数据构建对应子孔径下的轨迹运动误差粗补偿相位h
err_com1
(fr,ta)：
[0102][0103]
其中c为光速，fr表示距离频率，ta为方位时间，r
ref
(ta)表示对应方位时刻ta的瞬时斜距，且有
[0104]
[0105]
其中v表示平台速度，h为工作高度，rc表示场景中心斜距，xc与yc为根据载机运动方向建立笛卡尔坐标系下x轴与y轴的起始坐标，x
err
，y
err
与z
err
分别为根据惯导数据解算得到的x向、y向与z向的运动误差。将构建的粗补偿相位h
err_com1
(fr,ta)与信号相乘后，将信号变换回二维时域，通过对信号能量累加排序的方式筛选出强散射点样本，构建调频率项对其进行dechirp处理后沿方位向傅里叶变换，搜索方位向上能量最强点，计算出其对应的多普勒频率fd，进而可以反算得到相应的走动角θ
rmc
，即有
[0106]
θ
rmc
＝asin(fdλ/2v)
ꢀꢀꢀ
(10)
[0107]
λ表示波长，利用走动角θ
rmc
，即可构建线性走动补偿项h
lrmc
(fr，ta)
[0108][0109]
利用上式即可对脉压后的信号进行走动校正处理。
[0110]
(2)基于epga的振动误差估计
[0111]
epga自聚焦算法是一种非参数化的基于数据自适应地提取相位误差的方法，它能够提取任意频率成分的相位误差，具有较高的稳健性。本发明采用的epga算法采用“五步”法迭代处理流程：样本选择、循环移位、加窗滤波、相位梯度估计、迭代相位估计和相位补偿。考虑到epga算法是基于图像中某些特显点的聚焦情况来进行估计的，选择髙信杂比的距离单元数据，能够有效提高相位误差的估计精度与效率；挑选出合适的特显点样本后，通过循环移位将图像特显点移到图像的中间，进而消除线性相位的影响；随后基于一定的准则计算选择自适应窗长度，通过加窗处理将样本和窗外的杂波分离，进而保护样本的相位历程，并且可通过不断减小自适应窗的长度降低杂波的干扰，提高相位估计的精度；在进行相位梯度估计时，可以采用不同的相位梯度估计因子，如极大似然估计因子和线性无偏变化最小估计因子对相位梯度进行估计；对估计得到的相位梯度进行积分，得到相位误差，并通过线性拟合去除相位误差的线性分量，重复进行循环移位、加窗滤波、相位梯度估计操作，直到相位误差估计达到收敛。
[0112]
(3)子孔径划分及拼接
[0113]
本发明所采用的前两项技术均是在子孔径划分的基础上实施的，整体的技术思路是：首先将距离脉压后的回波数据沿方位维将其分为n个子孔径，每个子孔径长度为m，其中子孔径间的重叠量为m/2，然后采用pga自聚焦算法提取每个子孔径回波数据的相位误差矢量，并将得到的n个长度为m的相位误差矢量通过线性拟合的方式拼接成总长度为(n+1)m/2的相位误差矢量，最后通过高通滤波器对该相位误差矢量进行滤波处理，从而得到高频相位误差，并将其补偿到回波数据中。
[0114]
如图3所示，其具体实现步骤如下：
[0115]
1)设置子孔径长度为m和子孔径个数n，子孔径间重叠量为m/2；
[0116]
2)采用pga自聚焦算法提取每个子孔径回波数据的相位误差矢量：
[0117]
ωn＝[ω
n,1
,ω
n,2
,
…
,ω
n,m
,
…
,ω
n,m
],n＝1,2,
…
,n；m＝1,2,
…
,m；
[0118]
其中n表示第n个子孔径，m表示从某个子孔径中第m个脉冲回波数据提取出的相位误差。
[0119]
3)令ωn＝[ω
n,1
,ω
n,2
,
…
,ω
n,m
]、ω
n+1
＝[ω
n+1,1
,ω
n+1,2
,
…
,ω
n+1,m
]分别表示由第n个和第n+1个子孔径回波数据估计得到的相位误差矢量，其中ω
′n＝[ω
n,m/2+1
,
…
,
ω
n,m
]、ωn+1＝[ω
n+1,1
,
…
,ω
n+1,m/2
]为两个子孔径间相位误差矢量的重叠部分，利用线性表达式：y＝kx+b，其中y＝ω
′
n-ω
′
n+1
，x＝1,2,
…
,m/2，通过线性拟合的方式得到拟合系数k和b；
[0120]
4)利用3)步骤得到的线性拟合系数k和b，对第n+1个子孔径的相位误差矢量进行修正，使之与第n个子孔径的相位误差矢量保持线性连续，则修正后的第n+1个子孔径相位误差矢量为：其中
[0121]
5)n从1开始，并将修正后的第n+1个子孔径相位误差矢量与第n+2个子孔径相位误差矢量ω
n+2
重复3)到4)步骤，直到n个子孔径相位误差矢量全部修正完毕，子孔径相位拟合与修正示意图如图2所示；
[0122]
6)将第1个子孔径的相位误差矢量ω1与修正后(n-1)个子孔径相位误差矢量的后半段进行拼接，得到全孔径的相位误差矢量ω，其长度为m+(n-1)m/2＝(n+1)m/2；
[0123]
7)对相位误差矢量ω进行高通滤波，假设滤波器系数为γ，高通滤波后的高频相位误差矢量为其中表示卷积操作；
[0124]
8)利用全孔径相位误差矢量对回波数据进行相位补偿。
[0125]
以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明公开的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。