未知发射机位置和信号传播速度的椭圆定位方法

1.本发明涉及一种目标定位技术，尤其是涉及一种未知发射机位置和信号传播速度的椭圆定位方法。


背景技术：

2.目标定位不仅在声纳、传感器网络等科技领域有着广泛的应用，而且它在人员及军事安全方面也有着很大用处，比如在对受险人员的援救、对罪犯电子设备的定位，以及在军事中探测敌方目标的入侵、运动方向等方面起着重要作用。
3.目标定位通过收集发射机和接收机之间的交互信息以及一些已知位置的接收机的信息，然后运行定位算法完成目标的定位。用时间信息对目标位置进行定位的技术因为其精度高的特点而被研究人员广泛关注。椭圆定位就是基于时间信息的定位技术，其原理是通过寻找若干椭圆(二维)或椭球(三维)的交点来估计目标位置。每一个椭圆(椭球)都是由一个发射机和一个接收机组成，这样多个椭圆(椭球)的交点就是要被定位的目标位置。
4.在存在一个发射机、一个目标以及多个接收机的定位系统中，发射机发射一个信号，信号经由两条路径被接收机接收，一条是直接路径：发射的信号直接被接收机接收；另一条是间接路径：发射的信号先由目标反射然后被接收机接收。如果发射机的位置是已知的，那么因直接路径模型不包含关于目标的信息，只需通过间接路径模型去定位目标位置。然而在现实情况中，发射机的位置可能是未知，例如在全球定位系统通信很差的时候，不能提供发射机的位置。而更进一步，在发射机的位置未知且信号传播处于受到干扰的情况，即信号传播速度受到干扰而不能准确获得，例如水下通信或者在某些地下干扰环境，在这种情况下，现有文献中的目标定位方法几乎都无法适用。因此，有必要研究一种在发射机位置和信号传播速度未知的条件下联合估计目标和发射机的位置的方法。


技术实现要素：

5.本发明所要解决的技术问题是提供一种未知发射机位置和信号传播速度的椭圆定位方法，其无需知道发射机位置的先验信息，且在未知信号传播速度的情况下就能够精确地定位出目标的位置。
6.本发明解决上述技术问题所采用的技术方案为：一种未知发射机位置和信号传播速度的椭圆定位方法，其特征在于包括以下步骤：
7.步骤1：在多输入多输出雷达系统中，建立一个平面坐标系或空间坐标系作为参考坐标系，并设定存在n个用于接收信号的接收机、一个用于发射信号的发射机和一个目标，且设定发射机和接收机时钟同步，发射机在参考坐标系中的真实坐标位置未知，目标在参考坐标系中的真实坐标位置未知，n个接收机在参考坐标系中的真实坐标位置已知，将发射机在参考坐标系中的真实坐标位置记为to，将目标在参考坐标系中的真实坐标位置记为uo，将第j个接收机在参考坐标系中的真实坐标位置记为sj；其中，参考坐标系为平面坐标系时n≥3，参考坐标系为空间坐标系时n≥4，1≤j≤n；
8.步骤2：将发射机发射的信号直接被第j个接收机接收的时延的测量值记为τ
d,j
，将发射机发射的信号经过目标反射后被第j个接收机接收的时延的测量值记为τ
r,j
；然后将τ
d,j
的直接路径模型表示为：1≤j≤n，将τ
r,j
的间接路径模型表示为：1≤j≤n；其中，co表示发射机发射信号的信号传播速度，符号“|| ||”为求欧几里德范数符号，δτ
d,j
表示发射机发射的信号直接被第j个接收机接收的情况下信号传播路径上的测量噪声，δτ
r,j
表示发射机发射的信号经过目标反射后被第j个接收机接收的情况下信号传播路径上的测量噪声；
9.步骤3：对τ
d,j
的直接路径模型1≤j≤n进行转换，先等式两边乘以co，然后等式两边平方，再忽略二阶噪声项后得到1≤j≤n；并对τ
r,j
的间接路径模型1≤j≤n进行转换，先等式两边乘以co，然后将||u
o-to||移到等式左边，得到coτ
r,j-||u
o-to||＝||u
o-sj||+coδτ
r,j
,1≤j≤n，再对coτ
r,j-||u
o-to||＝||u
o-sj||+coδτ
r,j
,1≤j≤n等式两边平方并忽略二阶噪声项得到1≤j≤n；然后令将分别代入1≤j≤n和1≤j≤n中，对应得到1≤j≤n和1≤j≤n；其中，上标“t”表示向量的转置，ε
d,j
和ε
r,j
均为引用的中间变量，ε
d,j
＝coδτ
d,j
，ε
r,j
＝coδτ
r,j
，α为比例因子且α＞0，为引用的中间变量；
10.步骤4：根据1≤j≤n和1≤j≤
n，构建带有约束的加权最小二乘问题，描述为：其中，min()表示最小化函数，s.t.表示“受约束于”，，b、br和bd均为引入的中间向量，且已知，s1表示第1个接收机在参考坐标系中的真实坐标位置，sn表示第n个接收机在参考坐标系中的真实坐标位置，ar＝[a
r1
,
…
,a
rn
]，a
r1
和a
rn
根据得到，0k表示长度为k且元素的值全为0的列向量，ad＝[a
d1
,
…
,a
dn
]，a
d1
和a
dn
根据得到，a、ar和ad均为引入的中间矩阵，且已知，a
r1
和a
rn
、a
d1
和a
dn
均为引入的中间向量，且已知，b＝blkdiag(br,bd)，br＝diag(||u
o-s1||,
…
,||u
o-sn||)，bd＝diag(||s
1-to||,
…
,||s
n-to||)，blkdiag()表示生成以矩阵块为对角线的矩阵，diag()表示生成对角线矩阵，w、b、br、bd和均为引入的中间矩阵，δτ表示测量噪声向量，δτ服从均值为0、协方差矩阵为q
τ
的高斯分布，δτr＝[δτ
r,1
,
…
,δτ
r,n
]
t
，δτd＝[δτ
d,1
,
…
,δτ
d,n
]
t
，δτr和δτd均为引入的中间向量，δτ
r,1
表示发射机发射的信号经过目标反射后被第1个接收机接收的情况下信号传播路径上的测量噪声，δτ
r,n
表示发射机发射的信号经过目标反射后被第n个接收机接收的情况下信号传播路径上的测量噪声，δτ
d,1
表示发射机发射的信号直接被第1个接收机接收的情况下信号传播路径上的测量噪声，δτ
d,n
表示发射机发射的信号直接被第n个接收机接收的情况下信号传播路径上的测量噪声，q
τ
表示δτ的协方差矩阵，y表示引入的优化变量，y为维数为(2k+5)
×
1的列向量，k表示参考坐标系的维度，若参考坐标系为平面坐标系则k＝2，若参考坐标系为空间坐标系则k＝3，y
(2k+1)
表示y的第2k+1个元素，y
(2k+2)
表示y的第2k+2个元素，y
(2k+3)
表示y的第2k+3个元素，y
(2k+4)
表示y的第2k+4个元素，y
(2k+5)
表示y的第2k+5个元素，y
(1:k)
表示y的第1个到第k个元素组成的向量，y
(k+1:2k)
表示y的第k+1个到第2k个元素组成的向量；
[0011]
步骤5：令y＝yy
t
，并使用半正定松弛技术将步骤4中的带有约束的加权最小二乘
问题松弛为凸的半正定规划问题，描述为：其中，y为引入的辅助变量，tr()表示求矩阵的迹，y
(2k+4，2k+4)
表示y的第2k+4行第2k+4列元素，y
(2k+1，2k+5)
表示y的第2k+1行第2k+5列元素，y
(1:k,1:k)
表示y中从第1行到第k行和从第1列到第k列的所有元素构成的矩阵，y
(k+1:2k,k+1:2k)
表示y中从第k+1行到第2k行和从第k+1列到第2k列的所有元素构成的矩阵，y
(1:k,k+1:2k)
表示y中从第1行到第k行和从第k+1列到第2k列的所有元素构成的矩阵；
[0012]
步骤6：在步骤5中的凸的半正定规划问题中添加惩罚项y
(i,i)
，得到带惩罚项的半正定规划问题，描述为：其中，10
λ
为惩罚项系数，λ表示惩罚项系数的指数；
[0013]
步骤7：采用内点法求解带惩罚项的半正定规划问题，得到uo的近似全局最优解和to的近似全局最优解，对应作为uo的最终估计值和to的最终估计值，对应记为和和
[0014]
所述的步骤2中，直接路径为发射机发射的信号直接被接收机接收的情况下的信号传播路径，间接路径为发射机发射的信号经过目标反射后被接收机接收的情况下的信号传播路径。
[0015]
所述的步骤2中，时延通过接收机记录的接收到的信号的时间戳计算得到。
[0016]
所述的步骤6中，y
(i,i)
的获取过程为：采用内点法求解
得到y和y的解，对应记为y
*
和y
*
；然后计算y
*-y
*
(y
*
)
t
；再将y
*-y
*
(y
*
)
t
的计算结果的主对角线上最大的值作为y
(i,i)
。
[0017]
所述的步骤6中，λ的获取过程为：
[0018]
步骤6_1：设定λ的取值范围为[θ1,θ2]；然后令λ＝θ1；其中，θ1的初始值为-9，θ2的值为1；
[0019]
步骤6_2：采用内点法求解得到y的解，记为然后计算的秩；再判断的秩是否为1，如果是，则将得到时的λ的取值作为λ的最优值；否则，执行步骤6_3：
[0020]
步骤6_3：令θ1＝λ，然后返回步骤6_2继续执行，若在λ的取值范围内不存在使y的解的秩为1，则找出秩最接近1时y的解对应的λ的取值，作为λ的最优值。
[0021]
与现有技术相比，本发明的优点在于：
[0022]
1)本发明方法考虑了发射机位置未知且信号是处于干扰状态无法得知信号传播速度，更贴近现实应用。
[0023]
2)本发明方法在对惩罚项系数的指数选取上能够自适应地选择，无需重复人为操作，能达到对目标位置的精确估计。
[0024]
3)本发明方法对目标定位采用半正定规划方法进行处理，使本发明方法的定位性能有很好的稳定性，在恶劣情况下依旧能很好的定位目标位置。
附图说明
[0025]
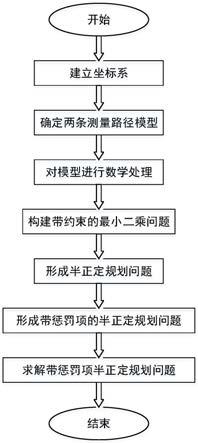
图1为本发明方法的流程框图；
[0026]
图2为在平面坐标系中存在一个发射机、一个目标和三个接收机时的模型图；
[0027]
图3为未知发射机位置和信号传播速度下，二维场景中存在一个发射机和六个接收机，本发明方法及无惩罚的半正定松弛方法、最大似然法估计和克拉美-罗下界对定位目标位置的对数均方误差(mse)随测量噪声功率增加的比较图；
[0028]
图4为未知发射机位置和信号传播速度下，二维场景中存在一个发射机和六个接收机，本发明方法及无惩罚的半正定松弛方法、最大似然法估计和克拉美-罗下界对定位发射机位置的对数均方误差随测量噪声功率增加的比较图。
具体实施方式
[0029]
以下结合附图实施例对本发明作进一步详细描述。
[0030]
本发明提出的一种未知发射机位置和信号传播速度的椭圆定位方法，其流程框图如图1所示，其包括以下步骤：
[0031]
步骤1：在多输入多输出(mimo)雷达系统中，建立一个平面坐标系或空间坐标系作为参考坐标系，并设定存在n个用于接收信号的接收机、一个用于发射信号的发射机和一个目标，且设定发射机和接收机时钟同步，发射机在参考坐标系中的真实坐标位置未知，目标在参考坐标系中的真实坐标位置未知，n个接收机在参考坐标系中的真实坐标位置已知，将发射机在参考坐标系中的真实坐标位置记为to，将目标在参考坐标系中的真实坐标位置记为uo，将第j个接收机在参考坐标系中的真实坐标位置记为sj；其中，参考坐标系为平面坐标系时n≥3，参考坐标系为空间坐标系时n≥4，1≤j≤n。
[0032]
图2给出了在平面坐标系中存在一个发射机、一个目标和三个接收机时的模型图。
[0033]
步骤2：将发射机发射的信号直接被第j个接收机接收的时延(即发射机发射信号到接收机接收信号的信号传播时间)的测量值记为τ
d,j
，将发射机发射的信号经过目标反射后被第j个接收机接收的时延(发射机发射的信号到目标的信号传播时间与从目标到接收机接收的信号传播时间之和)的测量值记为τ
r,j
，将发射机发射的信号直接被n个接收机接收的时延的测量值构成的向量记为τd，τd＝[τ
d,1
,
…
,τ
d,n
]
t
，将发射机发射的信号经过目标反射后被n个接收机接收的时延的测量值构成的向量记为τr，τr＝[τ
r,1
,
…
,τ
r,n
]
t
；然后将τ
d,j
的直接路径模型表示为：1≤j≤n，将τ
r,j
的间接路径模型表示为：1≤j≤n；其中，τ
d,1
表示发射机发射的信号直接被第1个接收机接收的时延的测量值，τ
d,n
表示发射机发射的信号直接被第n个接收机接收的时延的测量值，τ
r,1
表示发射机发射的信号经过目标反射后被第1个接收机接收的时延的测量值，τ
r,n
表示发射机发射的信号经过目标反射后被第n个接收机接收的时延的测量值，co表示发射机发射信号的信号传播速度，co未知，符号“|| ||”为求欧几里德范数符号，δτ
d,j
表示发射机发射的信号直接被第j个接收机接收的情况下信号传播路径上的测量噪声，δτ
r,j
表示发射机发射的信号经过目标反射后被第j个接收机接收的情况下信号传播路径上的测量噪声。
[0034]
在本实施例中，步骤2中，直接路径为发射机发射的信号直接被接收机接收的情况下的信号传播路径，间接路径为发射机发射的信号经过目标反射后被接收机接收的情况下的信号传播路径；时延通过接收机记录的接收到的信号的时间戳计算得到。
[0035]
步骤3：对τ
d,j
的直接路径模型1≤j≤n进行转换，先等式两边乘以co，然后等式两边平方，再忽略二阶噪声项(由于远远小于||s
j-to||ε
d,j
，所以可以省略)后得到1≤j≤n；并对τ
r,j
的间接路径模型1≤j≤n进行转换，先等式两边乘以co，然后将||u
o-to||移到等式左边，得到coτ
r,j-||u
o-to||＝||u
o-sj||+coδτ
r,j
,1≤j≤n，再对coτ
r,j-||u
o-to||＝||u
o-sj||+coδτ
r,j
,1≤j≤n等式两边平方并忽略二阶噪声项得到1≤j≤n；然后令将分别代入1≤j≤n和1≤j≤n中，对应得到1≤j≤n和1≤j≤n；其中，上标“t”表示向量的转置，ε
d,j
和ε
r,j
均为引用的中间变量，ε
d,j
＝coδτ
d,j
，ε
r,j
＝coδτ
r,j
，α为比例因子且α＞0，在本实施例中取α＝500，引入比例因子有助于在求解半正定规划问题的时候避免数值问题，为引用的中间变量。
[0036]
步骤4：根据1≤j≤n和1≤j≤n，构建带有约束的加权最小二乘问题，描述为：
其中，min()表示最小化函数，s.t.表示“受约束于”，，b、br和bd均为引入的中间向量，且已知，s1表示第1个接收机在参考坐标系中的真实坐标位置，sn表示第n个接收机在参考坐标系中的真实坐标位置，ar＝[a
r1
,
…
,a
rn
]，a
r1
和a
rn
根据得到，0k表示长度为k且元素的值全为0的列向量，ad＝[a
d1
,
…
,a
dn
]，a
d1
和a
dn
根据得到，a、ar和ad均为引入的中间矩阵，且已知，a
r1
和a
rn
、a
d1
和a
dn
均为引入的中间向量，且已知，b＝blkdiag(br,bd)，br＝diag(||u
o-s1||,
…
,||u
o-sn||)，bd＝diag(||s
1-to||,
…
,||s
n-to||)，blkdiag()表示生成以矩阵块为对角线的矩阵，diag()表示生成对角线矩阵，w、b、br、bd和均为引入的中间矩阵，δτ表示测量噪声向量，δτ服从均值为0、协方差矩阵为q
τ
的高斯分布，δτr＝[δτ
r,1
,
…
,δτ
r,n
]
t
，δτd＝[δτ
d,1
,
…
,δτ
d,n
]
t
，δτr和δτd均为引入的中间向量，δτ
r,1
表示发射机发射的信号经过目标反射后被第1个接收机接收的情况下信号传播路径上的测量噪声，δτ
r,n
表示发射机发射的信号经过目标反射后被第n个接收机接收的情况下信号传播路径上的测量噪声，δτ
d,1
表示发射机发射的信号直接被第1个接收机接收的情况下信号传播路径上的测量噪声，δτ
d,n
表示发射机发射的信号直接被第n个接收机接收的情况下信号传播路径上的测量噪声，q
τ
表示δτ的协方差矩阵，y表示引入的优化变量，y为维数为(2k+5)
×
1的列向量，k表示参考坐标系的维度，若参考坐标系为平面坐标系则k＝2，若参考坐标系为空间坐标系则k＝3，y
(2k+1)
表示y的第2k+1个元素，y
(2k+2)
表示y的第2k+2个元素，y
(2k+3)
表示y的第2k+3个元素，y
(2k+4)
表示y的第2k+4个元素，y
(2k+5)
表示y的第2k+5个元素，y
(1:k)
表示y的第1个到第k个元素组成的向量，y
(k+1:2k)
表示y的第k+1个到第2k个元素组成的向量。
[0037]
在此，通过对直接路径模型和间接路径模型转化形成了带有约束的加权最小二乘问题，构建的带有约束的加权最小二乘问题为下一步使用半正定松弛技术形成凸的半正定规划问题奠定了基础。
[0038]
步骤5：令y＝yy
t
，并使用半正定松弛技术将步骤4中的带有约束的加权最小二乘
问题松弛为凸的半正定规划问题，描述为：其中，y为引入的辅助变量，tr()表示求矩阵的迹，y
(2k+4，2k+4)
表示y的第2k+4行第2k+4列元素，y
(2k+1，2k+5)
表示y的第2k+1行第2k+5列元素，y
(1:k,1:k)
表示y中从第1行到第k行和从第1列到第k列的所有元素构成的矩阵，y
(k+1:2k,k+1:2k)
表示y中从第k+1行到第2k行和从第k+1列到第2k列的所有元素构成的矩阵，y
(1:k,k+1:2k)
表示y中从第1行到第k行和从第k+1列到第2k列的所有元素构成的矩阵。
[0039]
通过引入辅助变量y＝yy
t
将带有约束的加权最小二乘问题进行转化，然后利用半正定松弛技术对非凸约束进行松弛，进而形成一个凸的半正定规划问题。
[0040]
步骤6：在步骤5中的凸的半正定规划问题中添加惩罚项y
(i,i)
，得到带惩罚项的半正定规划问题，描述为：其中，10
λ
为惩罚项系数，λ表示惩罚项系数的指数。
[0041]
在本实施例中，步骤6中，y
(i,i)
的获取过程为：采用内点法求解
得到y和y的解，对应记为y
*
和y
*
；然后计算y
*-y
*
(y
*
)
t
；再将y
*-y
*
(y
*
)
t
的计算结果的主对角线上最大的值作为y
(i,i)
。
[0042]
在本实施例中，步骤6中，λ的获取过程为：
[0043]
步骤6_1：设定λ的取值范围为[θ1,θ2]；然后令λ＝θ1；其中，θ1的初始值为-9，θ2的值为1；λ的取值区间[-9,1]是在本方案的基础上确立的，λ的取值区间的不同对最终的估计精度有一定影响，但并非为关键。
[0044]
步骤6_2：采用内点法求解得到y的解，记为然后计算的秩；再判断的秩是否为1，如果是，则将得到时的λ的取值作为λ的最优值；否则，代表惩罚力度不够大，需增大λ的取值，执行步骤6_3。
[0045]
步骤6_3：令(运用二分法)，θ1＝λ，然后返回步骤6_2继续执行，若在λ的取值范围内不存在使y的解的秩为1，则找出秩最接近1时y的解对应的λ的取值，作为λ的最优值。
[0046]
在实际操作时为了得到更精确的λ值，可以在第一次达到y的解的秩为1时不结束，等到第二次达到y的解的秩为1时将对应的λ的取值作为λ的最优值。
[0047]
在将非凸约束丢掉后，会导致松弛得到的半正定规划问题不够紧，求不到全局最优解，因而通过添加惩罚项，让问题变得更紧，进而形成一个带惩罚项的半正定规划问题。
[0048]
步骤7：采用内点法求解带惩罚项的半正定规划问题，得到uo的近似全局最优解和
to的近似全局最优解，对应作为uo的最终估计值和to的最终估计值，对应记为和和
[0049]
为验证本发明方法的可行性和有效性，对本发明方法进行仿真的仿真试验结果如下：
[0050]
假设在二维空间即平面坐标系中有多个接收机和一个发射机，其真实坐标位置[x1,x2]
t
被随机产生，x1∈(-1000,1000)米、x2∈(-1000,1000)米；目标的真实坐标位置设置为[500,800]
t
米，测量噪声是相关的且协方差矩阵为q
τ
，信号传播速度co的真实值均匀分布在(1450,1500)米/秒范围内，比例因子α＝500。
[0051]
测试本发明方法的性能选择的对比方法有无惩罚的半正定松弛方法(即在本发明方法的步骤6中不添加惩罚项时形成的方法，简称为sdp)和最大似然法(简称为mle)。
[0052]
图3给出了未知发射机位置和信号传播速度下，二维场景中存在一个发射机和六个接收机，本发明方法(penalized sdp)及无惩罚的半正定松弛方法、最大似然法估计和克拉美-罗下界(crlb)对定位目标位置的对数均方误差(mse)随测量噪声功率增加的比较图，图3中的横坐标是对测量噪声功率取对数，纵坐标是对估计目标位置的均方误差取对数。从图3中可以看出，本发明方法有着非常好的性能表现，本发明方法在大噪声的情况下也基本可以达到克拉美-罗下界精度，而无惩罚的半正定松弛方法即便在小噪声的情况下也不能达到其精度。
[0053]
图4给出了未知发射机位置和信号传播速度下，二维场景中存在一个发射机和六个接收机，本发明方法(penalized sdp)及无惩罚的半正定松弛方法、最大似然法估计和克拉美-罗下界对定位发射机位置的对数均方误差随测量噪声功率增加的比较图。图4中的横坐标是对测量噪声功率取对数，纵坐标是对估计发射机位置的均方误差(mse)取对数。从图4中可以看出，本发明方法维持了发射机位置估计的性能。