基于密度锥削阵的FDA-MIMO抗随队干扰方法

基于密度锥削阵的fda-mimo抗随队干扰方法
技术领域
1.本发明属于雷达抗干扰技术领域，涉及基于密度锥削阵的 fda-mimo抗随队干扰方法。


背景技术：

2.随队干扰机在掩护作战飞机突防时，与干扰机处于角度维接近但 距离维可分的空间位置，我方雷达可通过空域滤波技术实现对干扰方 向的增益置零从而抑制敌方的干扰施放。频率分集阵列雷达通过改变 载波频率和频偏增量可以离散方式扫描空间中的每个点，提供了极大 的电子反对抗应用潜力。现今广泛应用的相控阵雷达技术在抑制目标 与干扰同时落入主瓣的干扰时，其阵列方向图会出现主瓣分裂、波束 形成器性能下降的问题。


技术实现要素：

3.本发明的目的是提供基于密度锥削阵的fda-mimo抗随队干扰 方法，解决了现有的相控阵雷达电扫描技术在抑制随队干扰中出现的 主瓣畸变、波束形成器性能下降的问题。
4.本发明所采用的技术方案是，基于密度锥削阵的fda-mimo抗 随队干扰方法，具体按照以下步骤实施：
5.步骤1、构造fda-mimo阵列结构；
6.步骤2、以采用非线性频控函数密度锥削阵代替一维均匀线性阵 列，构造基于密度锥削阵的fda-mimo阵列结构；
7.步骤3、采用改进的自适应波束形成算法修正导向矢量。
8.本发明的特点还在于，
9.步骤1的具体步骤为，构造一部由n个阵元组成的一维均匀线 性fda阵列，n表示一维均匀线性fda阵列的阵元总数；
10.步骤1.1、设一维均匀线性fda阵列参考阵元0的载波频率为f0， 相邻阵元间的频偏增量为δf，则一维均匀线性fda阵列中第n个阵 元对空辐射信号的载波频率fn为：
11.fn＝f0+nδf,n＝0,1,2,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)；
12.步骤1.2、在t时刻，窄带条件下一维均匀线性fda阵列中第n 个阵元的对空辐射信号sn(t)为：
13.sn(t)＝exp(j2πfnt),n＝0,1,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(2)；
14.步骤1.3、对空辐射信号sn(t)加权得到s
rn
(t)，使其到达远场目标 点(r0,θ0)：
[0015][0016]
式(3)中，(r0,θ0)为远场目标点的坐标，r为参考阵元到目标 点的距离，d为一维均
匀线性fda阵列相邻阵元的间距，θ为一维均 匀线性fda阵列主波束指向与阵列法线方向的夹角，j表示虚数单位， 为c为光速；
[0017]
步骤1.4、对空辐射信号的经远场目标点进行二次反射，得到被 一维均匀线性fda阵列的第m个阵元接收的信号rm(t；θ0,r0)为：
[0018][0019]
步骤1.5、在一维均匀线性fda阵列的每一个接收通道中通过n 个窄带滤波器对第m个阵元接收到的所有信号进行分离，再对分离 后的回波数据按接收通道进行重排，得到数据大小为n
×
n的信号， 通过对重排后的信号进行普通波束扫描，得到阵列输出结果 y(t；θ0,r0)，即得到fda-mimo阵列结构：
[0020][0021]
步骤2具体为：
[0022]
步骤2.1、改变一维线性阵列中阵元的排布方式，一维密度锥削 阵列结构中以a(1≤a≤1+δ,δ＝0～0.2)表示密度锥削阵阵元间距 递增因子，则一维线性阵列中第n个阵元到一维线性阵列中参考阵元 0的间距为ζn为间隔因子，xm＝km，k≤0.5；
[0023]
步骤2.2、在改变一维线性阵列阵元排布方式的基础上，对一维 线性阵列第n个阵元的阵列载波频率进行修正，修正为：
[0024]fn
＝f0+sin(n)δf,n＝0,1,2,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)；
[0025]
从而实现阵列方向图的距离-角度解耦，得到相比于步骤1一维 均匀线性fda阵列性能更优的阵列方向图。
[0026]
步骤3具体过程为：
[0027]
步骤3.1、由n个阵元组成的一维密度锥削fda阵列，阵列的 接收信号x(t)为：
[0028][0029]
式(7)中，θ0表示远场目标点的角度坐标，远场目标点的坐标 为(r0,θ0)，q表示干扰源的总数，干扰源的空间坐标分别为 (r
l
,θ
l
),l＝1,2,...,q，i
l
(t),l＝1,2,...,q表示干扰信号，a(θ
l
)表示空 间位置(r
l
,θ
l
),l＝1,2,...,q处的导向矢量，空间位置(r0,θ0)处的导向 矢量a(θ0)为：
[0030][0031]
a(θ
l
)为：
[0032][0033]
阵列的输出为：
[0034][0035]
式(10)中，w表示权矢量，h表示共轭转置运算符，n(t)表示 噪声；
[0036]
步骤3.2、假定导向矢量及真实导向矢量失配的情况下，通过搜 索方法求得真实的导向矢量，得约束条件为：
[0037][0038]
式(11)中，为假定的期望信号导向矢量，a为真实的信号导 向矢量，以权矢量为自变量使用拉格朗日乘子法构造代价函数j：
[0039][0040]
式(12)中，r表示协方差矩阵，λ表示拉格朗日乘子，h表示 共轭转置运算符，-1
表示矩阵求逆运算符，ε为一个取值较小的常数， 取ε＝1.5。
[0041]
步骤3.2采用牛顿法沿负梯度方向进行搜索得导向矢量的迭代公 式：
[0042][0043]
式(13)中，μ表示步长因子，表示估计协方差矩阵，可由阵 列接收信号x(t)递推得到由 可近似为w(n+1)可知，导向矢量的最终迭代公式为：
[0044][0045]
式(14)中，拉格朗日乘子λ在每次迭代中需要进行更新，a(n+1) 满足满足约束条件令b1＝a(n)-2μw(n+1)， 求解式(15)所示的一元二次方程可得λ：
[0046]
a1λ2+a2λ+a3＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0047]
式(15)中一元二次方程的系数如式(16)～式(18)所示：
[0048][0049][0050][0051]
本发明的有益效果是，本发明基于密度锥削阵的fda-mimo抗 随队干扰方法，在频
率分集阵列(frequency diverse array,fda)方 向图距离-角度解耦技术的基础上，使用密度锥削阵代替现有技术中 基本的一维均匀线性阵列结构，解决了现有的相控阵雷达电扫描技术 在抑制随队干扰中出现的主瓣畸变、波束形成器性能下降的问题，提 高了抗随队干扰的能力。
附图说明
[0052]
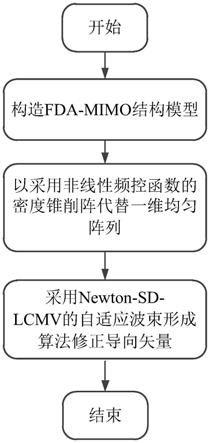
图1是本发明基于密度锥削阵的fda-mimo抗随队干扰方法的 流程图；
[0053]
图2是本发明采用一维均匀线性fda阵列结构图；
[0054]
图3是本发明采用非线性频控函数的密度锥削阵fda阵列结构 图；
[0055]
图4是本发明相控阵的发射方向图；
[0056]
图5是本发明一维均匀线性fda的发射方向图；
[0057]
图6是本发明密度锥削阵fda的发射方向图；
[0058]
图7是本发明基于lcmv算法的相控阵阵列方向图；
[0059]
图8是本发明基于lcmv算法的fda-mimo阵列方向图；
[0060]
图9是本发明基于改进算法的密度锥削fda阵列方向图；
[0061]
图10是本发明基于lcmv算法的相控阵阵列方向图；
[0062]
图11是本发明基于lcmv算法的fda-mimo阵列方向图；
[0063]
图12是本发明基于改进的算法的密度锥削fda阵列方向图；
[0064]
图13是本发明基于lcmv算法的相控阵阵列方向图；
[0065]
图14是本发明基于lcmv算法的fda-mimo阵列方向图；
[0066]
图15是本发明基于改进算法的密度锥削fda阵列方向图。
具体实施方式
[0067]
下面结合附图和具体实施方式对本发明进行详细说明。
[0068]
本发明基于密度锥削阵的fda-mimo抗随队干扰方法，如图1 所示，具体按照以下步骤实施：
[0069]
步骤1、构造fda-mimo阵列结构；
[0070]
步骤1的具体步骤为，如图2所示，构造一部由n个阵元组成 的一维均匀线性fda阵列，n表示一维均匀线性fda阵列的阵元总 数。
[0071]
步骤1.1、设一维均匀线性fda阵列参考阵元0的载波频率为f0， 相邻阵元间的频偏增量为δf，则一维均匀线性fda阵列中第n个阵 元对空辐射信号的载波频率fn为：
[0072]fn
＝f0+nδf,n＝0,1,2,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)；
[0073]
步骤1.2、在t时刻，窄带条件下一维均匀线性fda阵列中第n 个阵元的对空辐射信号sn(t)为：
[0074]
sn(t)＝exp(j2πfnt),n＝0,1,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(2)；
[0075]
步骤1.3、对空辐射信号sn(t)加权得到s
rn
(t)，使其到达远场目标 点(r0,θ0)：
[0076]
[0077]
式(3)中，(r0,θ0)为远场目标点的坐标，r为参考阵元到目标 点的距离，d为一维均匀线性fda阵列相邻阵元的间距，θ为一维均 匀线性fda阵列主波束指向与阵列法线方向的夹角，j表示虚数单位， 为c为光速。
[0078]
步骤1.4、对空辐射信号的经远场目标点进行二次反射，得到被 一维均匀线性fda阵列的第m个阵元接收的信号rm(t；θ0,r0)为：
[0079][0080]
步骤1.5、在一维均匀线性fda阵列的每一个接收通道中通过n 个窄带滤波器对第m个阵元接收到的所有信号进行分离，再对分离 后的回波数据按接收通道进行重排，得到数据大小为n
×
n的信号， 通过对重排后的信号进行普通波束扫描，得到阵列输出结果 y(t；θ0,r0)，即得到fda-mimo阵列结构：
[0081][0082]
步骤1得到的一维均匀线性fda阵列中，如图2所示，相邻阵 元的间距是相等的，采用这种排布方式的一维均匀线性fda阵列， 阵列方向图中存在距离-角度耦合引起的主波束指向多极值的问题， 进而会对抗随队干扰的效果产生不利的影响。
[0083]
步骤2、以采用非线性频控函数密度锥削阵代替一维均匀线性阵 列，构造基于密度锥削阵的fda-mimo阵列结构；
[0084]
步骤2.1、改变一维线性阵列中阵元的排布方式，如图3所示， 一维密度锥削阵列结构中以a(1≤a≤1+δ,δ＝0～0.2)表示密度锥 削阵阵元间距递增因子，则一维线性阵列中第n个阵元到一维线性阵 列中参考阵元0的间距为ζn为间隔因子，xm＝km， k≤0.5；
[0085]
步骤2.2、在改变一维线性阵列阵元排布方式的基础上，对一维 线性阵列第n个阵元的阵列载波频率进行修正，修正为：
[0086]fn
＝f0+sin(n)δf,n＝0,1,2,...,n-1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)；
[0087]
从而实现阵列方向图的距离-角度解耦，得到相比于步骤1一维 均匀线性fda阵列性能更优的阵列方向图。
[0088]
步骤3、采用改进的自适应波束形成算法修正导向矢量。
[0089]
步骤3针对基于线性约束最小方差准则(linearly constrainedminimum variance,lcmv)的自适应波束形成器出现的主瓣畸变、波 束形成器性能下降的问题，提出改进的自适应波束形成算法修正随队 干扰抑制过程中出现的导向矢量失配，提高抗随队干扰的能力。
[0090]
步骤3.1、由n个阵元组成的一维密度锥削fda阵列，阵列的 接收信号x(t)为：
[0091]
[0092]
式(7)中，θ0表示远场目标点的角度坐标，远场目标点的坐标 为(r0,θ0)，q表示干扰源的总数，干扰源的空间坐标分别为 (r
l
,θ
l
),l＝1,2,...,q，i
l
(t),l＝1,2,...,q表示干扰信号，a(θ
l
)表示空 间位置(r
l
,θ
l
),l＝1,2,...,q处的导向矢量，空间位置(r0,θ0)处的导向 矢量a(θ0)为：
[0093][0094]
a(θ
l
)为：
[0095][0096]
阵列的输出为：
[0097][0098]
式(10)中，w表示权矢量，h表示共轭转置运算符，n(t)表示 噪声；
[0099]
当先验已知的期望信号导向矢量与实际测得的导向矢量之间存 在失配时，lcmv自适应波束形成器会收敛到假定的导向矢量上，真 实的期望信号会被当作干扰抑制掉，从而导致主瓣畸变、波束形成器 性能下降。针对这一问题，在波达方向估计存在偏差。
[0100]
步骤3.2、假定导向矢量及真实导向矢量失配的情况下，通过搜 索方法求得真实的导向矢量，得约束条件为：
[0101][0102]
式(11)中，为假定的期望信号导向矢量，a为真实的信号导 向矢量，以权矢量为自变量使用拉格朗日乘子法构造代价函数j：
[0103][0104]
式(12)中，r表示协方差矩阵，λ表示拉格朗日乘子，h表示 共轭转置运算符，-1
表示矩阵求逆运算符，ε为一个取值较小的常数， 取ε＝1.5。
[0105]
采用牛顿法沿负梯度方向进行搜索得导向矢量的迭代公式：
[0106][0107]
式(13)中，μ表示步长因子，表示估计协方差矩阵，可由阵 列接收信号x(t)递推得到由 可近似为w(n+1)可知，导向矢量的最终迭代公式为：
[0108][0109]
式(14)中，拉格朗日乘子λ在每次迭代中需要进行更新，a(n+1) 满足满足约束条
件令b1＝a(n)-2μw(n+1)， 求解式(15)所示的一元二次方程可得λ：
[0110]
a1λ2+a2λ+a3＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0111]
式(15)中一元二次方程的系数如式(16)～式(18)所示：
[0112][0113][0114][0115]
实施例
[0116]
远场目标点位于(0
°
,100km)，如图4所示，为相控阵的发射方向 图，如图5所示，为一维均匀宪政fda阵列的发射方向图，如图6 所示，为采用正弦频控函数的密度锥削阵fda发射方向图。对比图 4、图5，图6中密度锥削阵fda可在目标点处形成单一的主波束指 向，且发射能量更集中、旁瓣更低。
[0117]
当远场目标点位于(0
°
,100km)，干扰位于(10
°
,120km)时，如图7、 图8、图9所示，分别为基于lcmv波束形成器的相控阵、fda-mimo 阵列结构和基于本技术的密度锥削fda阵列三种结构的干扰抑制性 能。由图7～9可知，当干扰与目标的位置在空间中距离较远时，三种 阵列结构得到的阵列方向图都能在目标位置处保持有效增益的同时 在干扰位置处实现置零。但相控阵的阵列方向图中的波束指向在距离 维无分辨能力，fda-mimo的阵列方向图中存在多极值的问题。
[0118]
当远场目标点位于(0
°
,100km)，干扰位于(3
°
,105km)时，如图10、 图11、图12所示，分别为基于lcmv算法的相控阵、fda-mimo 和本技术的密度锥削fda三种结构的干扰抑制性能。由图10～12可 知，当干扰与目标的位置在距离维可分同时在角度维接近时，相控阵 的阵列方向图会出现主瓣畸变、旁瓣升高的问题。与图11相比，图 12中密度锥削fda的阵列方向图在实现干扰位置置零、主波束增益 保持的同时，还有效消除了fda-mimo的阵列方向图中的多极值问 题。
[0119]
当远场目标点位于(0
°
,100km)，干扰1位于(3
°
,105km)，干扰2 位于(-3
°
,110km)，如图13、图14、图15所示，分别为基于lcmv 算法的相控阵、fda-mimo和基于本技术的密度锥削fda阵列三种 结构的干扰抑制性能。由图13～15可知，当存在两个干扰与目标的位 置在距离维可分同时在角度维接近时，相控阵的阵列方向图仍然出现 了主瓣畸变、且无法有效区分干扰2与目标。由于指向误差的存在， 图14和图13中主波束的指向出现了偏移，而图15可以实现对目标 方向增益的保持和干扰方向的有效置零，且图15同时消除了方向图 的多极值问题。