一种基于短时傅里叶变换数据的时差快速预测方法

1.本发明涉及一种基于短时傅里叶变换数据的时差快速预测方法，属于雷达目标探测信号处理领域。


背景技术：

2.对空中未知目标的探测与定位在现代雷达常规防空任务中具有重要意义。经过多年的研究，雷达对空目标探测与定位技术已取得了长足发展，各种军民雷达已被广泛应用。针对主动雷达，目前常用的测量雷达与目标之间距离的方法主要是通过回波相对于发射信号的延迟。根据雷达发射信号的不同，测定延迟时间通常可以采用脉冲法、频率法和相位法。针对被动雷达，由于被动雷达不发射信号只接收信号，无法得知电磁波离开目标的时间，难以直接计算出目标与接收站之间的距离，所以被动雷达测距一般需要多个观测站测量值来实现。常用的方法是利用多接收站同时测量空中目标发射电磁波信号的信号到达时间差来完成。多站时差定位法又称双曲线定位，已经成为现代无源定位技术中最具有发展前景的定位方法。另外，与主动雷达相比，被动雷达具有良好的四抗特性：对低空/超低空入侵目标检测能力，综合性电子干扰能力，对隐身目标的检测能力和抗反辐射导弹能力。此外，由于被动雷达利用探测空域已存在的辐射源信号，无需高功率发射机，只需要配备相应地接收设备，设备量小、成本低。因此，利用被动雷达对空中未知目标进行探测与定位成为当下研究的热点，且被广泛应用于机场、城市空中监视以及对重要地区的空域防御等。
3.目标发射电磁波信号到达两个侦测接收站的时间差构成一个双曲面(线)，多个双曲面(线)相交即可得到目标的位置。在这种定位方法中面临的一个主要问题是：能否对多站之间侦测接收信号进行快速时差计算，时差计算是目标定位过程中极其重要的一步。在被动雷达进行侦测空中电磁波信号过程中，雷达系统信号预处理步骤是对侦测接收到的电磁波信号通过短时傅里叶变换进行频谱分析，若发现频谱中存在特征信号(如步进频信号等)，即可判定存在空中目标活动。常规的雷达系统发现未知空中目标后会采取如下步骤进行时差计算，以两部被动雷达接收信号之间的时差求解为例：(1)将侦测接收到的两站时域信号进行快速傅里叶变换(fft)，将时域信号转换至频域；(2)将两路频域信号进行频域相乘；(3)将频域相乘得到的信号进行快速逆傅里叶变换(ifft)，完成快速时差计算。在此过程中，过程较为复杂，数据运算量巨大，耗费雷达系统有限的计算资源。因此，如何对侦测接收的电磁波信号进行快速时差计算是一个难点，需要展开研究，以提高雷达对未知空中目标快速定位的性能。


技术实现要素：

4.本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法的目的是：提供一种基于短时傅里叶变换的多部被动雷达侦测接收信号的时差快速预测方法，充分利用被动雷达系统短时傅里叶变换信号预处理过程所得的频谱信号，在保证相同准确度的前提下，简化信号处理流程，降低运算量，实现被动雷达对空中未知目标的快速定位。
5.本发明的目的是通过下述技术方案实现的。
6.本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法，通过直接利用回波信号预处理时的短时傅里叶变换所得到的频谱信号进行时差快速预测。当雷达系统探测到有效目标时，将预处理过程得到的两路频谱信号矩阵进行恒虚警检测后进行时频域复乘；再复乘所得的时频域信号矩阵沿着时间维进行叠加操作；将叠加所得到列信号进行快速逆傅里叶变换，完成时差快速预测。本发明充分利用被动雷达系统短时傅里叶变换信号预处理过程所得的频谱信号。与传统时差计算方法相比，在保证相同准确度的前提下，不仅简化信号处理流程，还降低运算量，提高目标定位的效率。
7.本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法，包括如下步骤：
8.步骤一：对采集到的两部雷达侦测到的回波信号s1(m)和s2(m)进行预处理操作和频谱监测，利用被动雷达系统短时傅里叶变换信号预处理过程所得的频谱信号进行频谱监测，对得到的两路频谱信号矩阵进行频谱分析，若频谱信号矩阵存在特征信号，则判断存在空中目标，进行步骤二。
9.步骤1.1：对侦测信号进行预处理操作，即基于短时傅里叶变换将两部雷达时域信号转变为时频域信号，分别对应得到s1(n,f)和s2(n,f)时频谱矩阵。
10.步骤1.2：若发现信号频谱中存在特征信号，即判定存在空中目标活动，则转至步骤二。
11.步骤1.3：若未发现信号频谱中存在特征信号，则继续进行频谱监测。
12.步骤1.2所述特征信号包括且不限于步进频信号、跳频信号、线性调频信号等。
13.步骤二：利用步骤一回波信号预处理时的短时傅里叶变换所得到的两路频谱信号矩阵s1(n,f)和s2(n,f)，进行恒虚警检测，保留超过门限的频谱信号矩阵数据，未超过门限的频谱信号数据置零，这样可以大大减少计算量。得到新的频谱矩阵s1(n,f)和s2(n,f)，并进行时频域复乘得到时频域复乘的时频域信号矩阵s
12
(n,f)。无需对两部雷达侦测到的时域回波信号转换为频域信号，而是直接对短时傅里叶变换后的频谱信号矩阵进行操作。
14.步骤2.1：进行恒虚警检测。根据雷达系统和环境噪声影响对检测门限进行合理估值，利用该门限对步骤一得到的两路频谱信号矩阵数据进行恒虚警检测，仅保留超过门限的频谱信号矩阵数据，对未超过门限的频谱信号矩阵数据进行置零操作，即得到新的频谱矩阵s1(n,f)和s2(n,f)。
15.步骤2.2：执行复共轭相乘运算。对s1(n,f)做复共轭运算得到s
1*
(n,f)，再将s
1*
(n,f)与s2(n,f)频谱矩阵对应位置元素相乘，得到s
12
(n,f)。
[0016][0017]
步骤三：对步骤二所得的时频域信号矩阵沿着时间维进行叠加操作，将叠加所得到列信号进行快速逆傅里叶变换，计算得到两部雷达时差结果，即基于短时傅里叶变换数据实现两部被动雷达侦测接收信号时差快速预测。
[0018]
步骤3.1：对s
12
(n,f)频谱矩阵进行沿着时间维进行叠加操作，得到s
12
(f)序列。
[0019]
步骤3.2：对s
12
(f)进行快速逆傅里叶变换，得到序列r
12
(n)。序列r
12
(n)的峰值所对应的时间为雷达接收站2相对于雷达接收站1的时差，即基于短时傅里叶变换数据实现两部被动雷达侦测接收信号时差快速预测。
[0020]
步骤四：基于步骤一至步骤三，在实现两部被动雷达侦测接收信号时差快速预测基础上，进一步实现实现多部被动雷达侦测接收信号时差快速预测。
[0021]
有益效果：
[0022]
1.与常规方法相比，本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法，直接使用基于短时傅里叶变换的雷达侦测回波信号频谱，在处理流程上直接省去将回波时域信号变到频域步骤，能够显著简化雷达信号处理流程，提高计算效率。
[0023]
2.本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法，利用基于短时傅里叶变换的雷达侦测回波信号频谱，对得到的站1和站2频谱共轭复乘信号后进行频谱矩阵沿着时间维进行叠加操作，再进行快速逆傅里叶变换完成时差计算。与常规方法相比，降低傅里叶变换过程数据运算量，显著降低整体算法的运算量，实现快速时差预测。
[0024]
3.本发明公开的一种基于短时傅里叶变换数据的时差快速预测方法，在实现两部被动雷达侦测接收信号时差快速预测基础上，进一步实现实现多部被动雷达侦测接收信号时差快速预测。
附图说明
[0025]
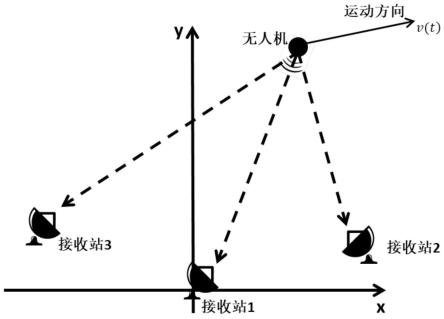
图1是本发明“一种基于短时傅里叶变换数据的时差快速预测方法”中实施例中的无线电侦测雷达系统示意图。
[0026]
图2是本发明“一种基于短时傅里叶变换数据的时差快速预测方法”中实施例中本发明算法流程图。
[0027]
图3是本发明“一种基于短时傅里叶变换数据的时差快速预测方法”中实施例中的两部雷达侦测接收信号时频谱图，其中图3(a)为站1接收信号时频图，图3(b)为站2接收信号时频图。
[0028]
图4是本发明“一种基于短时傅里叶变换数据的时差快速预测方法”中实施例中的时差结果图。
具体实施方式
[0029]
下面将结合附图及具体实例对本发明技术方案进行详细说明，需要指出的是，所描述的实施例仅旨在便于对本发明的理解，而不起任何限定作用。
[0030]
实施例1：
[0031]
本实施例阐述：将本发明“一种基于短时傅里叶变换数据的时差快速预测方法”使用仿真实例进行快速时差计算。
[0032]
本实施例中，仿真软件为matlab。空中目标辐射源发射波形相关参数如下：信号基带带宽8mhz，每10ms改变一次载频，载频从30mhz均匀跳变至70mhz，即30mhz，40mhz，50mhz，60mhz，70mhz，采样率为100mhz，信号总时间长度为50ms。本实施例中采用双站雷达结构如图1所示，含有一个空中辐射源，两部被动雷达接收系统，分别为站1雷达和站2雷达，组成双站对空探测雷达系统。设站1雷达系统和站2雷达系统都可以完整接收到空中辐射源发出的无线电信号。令设接收站2接收到的辐射源信号相对于接收站1延时30ns，以便进行时差仿真验证。
[0033]
步骤一、对接收站1和接收站2接收到的目标信号s1(m)和s2(m)做短时傅里叶变换，
设置短时傅里叶变换的窗函数w(m)为矩形窗，窗长w＝128，对于一个时间窗内的数据，使用快速傅里叶变换的方法进行计算，得到时频数据s1(n,f)和s2(n,f)，其中n表示离散时间，f表示离散频率。接收站1和接收站2的时频图如图3所示，在图(a)和图(b)中可以看出，接收站1和接收站2都完整接收到了信号，可看到明显的步进频频谱。
[0034]
步骤二、由于信号跳频，通过对信号频谱分析可得：同一载频有效数据时长为0～10ms、10～20ms、20～30ms、30～40ms、40～50ms，这里仅对前10ms有效数据进行分析，并分别对站1和站2获得的信号频谱进行恒虚警检测，得到有效数据，其他时段同频信号分析过程类似，不做赘述。对s1(n,f)取前10ms的数据进行恒虚警检测后做复共轭运算得到s
1*
(n,f)，将s
1*
(n,f)与s2(n,f)前10ms的有效数据矩阵对应位置元素相乘，得到s
12
(n,f)。
[0035]
步骤三、对s
12
(n,f)相同频率f的数据相加，即矩阵列相加操作，得到s
12
(f)，再对s
12
(f)进行快速傅里叶逆变换，得到时域相关序列r
12
(n)。r
12
(n)的峰值对应的延时为30ns，完成验证。验证结果如图4所示。
[0036]
运算量对比说明：接收到的每段信号长度为n＝2
p
，常规算法与本专利算法在计算时差之前都要对信号进行短时傅里叶变换进行时频检测，所以短时傅里叶变换不计入运算量的计算中。常规的相关序列频域计算方法需要做2次n点的fft，1次n点的乘法以及1次n点的ifft。则常规方法计算量为次复数乘法以及3
·n·
p次复数加法。而对于本专利提出的快速算法，窗长w＝2q，需要做一次两个n/w列w
′
行数据矩阵复数乘法，w
′
为有效频谱数据矩阵的列信号长度，一次n/w列w
′
行数据的累加，一次w
′
点的ifft，计算量为次复数乘法以及次复数加法。
[0037]
由于在数字信号处理系统中，复数乘法的运算时间远大于复数加法的运算时间，所以主要考虑复数乘法的运算量进行对比。在本实例中，n＝1
×
106个点，p≈20，q＝7，w对应128，w
′
＝12，则常规方法复数乘法运算量为32.5m次，其运算量随n的点数增大而增大。本发明专利复数乘法运算量为96k次。可以看出本专利算法的运算量远小于常规算法，比常规方法减小300多倍，证明了该算法的有效性。
[0038]
步骤四：基于步骤一至步骤三，在实现两部被动雷达侦测接收信号时差快速预测基础上，进一步实现实现多部被动雷达侦测接收信号时差快速预测。
[0039]
基于此，本发明提供一种基于短时傅里叶变换的多部被动雷达侦测接收信号的时差快速预测方法。通过直接利用基于短时傅里叶变换的多部被动雷达侦测接收信号，完成时差快速计算过程，实现对空中目标进行快速测距的目的。与传统时差计算方法相比，本发明将充分利用被动雷达系统信号预处理时的短时傅里叶变换所得到的频谱信号进行时差快速计算。在处理流程上直接省去将回波时域信号变到频域步骤。在保证相同准确度的前提下，能够极大简化雷达信号处理流程，提高预测效率。
[0040]
以上所述的具体描述，对发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。