一种构建土体冻结温度预测模型的方法与流程

1.本发明属于岩土工程技术领域，特别是冻土工程领域，特别涉及一种构建土体冻结温度预测模型的方法，用于预测土体的冻结温度。


背景技术：

2.土体的冻结温度是判定土体是否处于冻结状态的关键指标，也是判定冻结深度和人工冻结壁厚度的依据。另外，冻结温度也是土体冻结特征模型(未冻水含量、基质吸力)、冻土力学特性和冻土渗透特性中的重要参数。在寒区工程建设和人工冻结技术及冻结试验过程中，需要判断场地(或试样)的冻结进程，利用布设的温度传感器实时监测可实现无损判断温度场分布从而获得冻结空间分布。在当今人工冻结工程中，特别是隧道冻结施工、矿井作业和污染废料处理等领域，用于判断冻结是否到达预定目标厚度，动态调整冻结输入或输出，直接关系到工程建设的安全性。
3.对于特定的土体，其冻结温度受干密度和含水量的影响；对于不同的土体，受土体粒径成分含量(如黏粒、粉粒或砂粒等)、矿物质类别及含量、溶质类别及含量等多因素的影响，如果按照纯水的冻结温度作为土体的冻结温度将会引起较大误差。采用连续测试的方法测定冻结温度，一方面需要配备精准的传感器和数据采集设备，另一方面测试比较耗时、费力、效率低并且成本高，不便于快速获得冻结温度数值。本预测模型可在知道含水量和干密度两个基本的宏观物理量条件下，快速准确地预测土体冻结温度。


技术实现要素：

4.本发明提供了一种构建土体冻结温度预测模型的方法，能快速预测不同物理状态土体冻结温度。
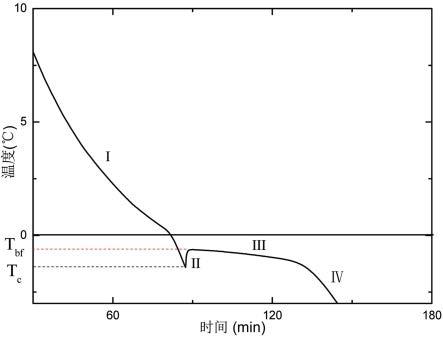
5.本方法能基于较少测试结果(最少3组)快速得出不同连续物理状态(如含水量和干密度)的冻结温度。研究表明，土体的冻结温度不受冻结速率和冻结环境温度大小的影响。冻结过程中，土体的温度因相变潜热的释放而表现出温度跳跃，土体的降温过程总体上也分为四个阶段：降温至过冷阶段(ⅰ)、升温跳跃阶段(ⅱ)、稳定阶段(ⅲ)、降温阶段(ⅳ)，如图1所示。阶段ⅰ的终点、阶段ⅱ的起点对应的温度称为过冷温度tc，阶段ⅱ的终点、阶段ⅲ的起点即温度因潜热释放后的跳跃温度t
bf
称为冻结温度。对于冻结温度的测定一般根据相变物体的降温时程曲线获得，并将t
bf
作为本测试物品此种物理状态下的冻结温度。
6.1)、制备至少三组不同含水量的土样，记为ω1、ω2
……
ωn(n≥3)，将其按照目标干密度制备测试土样，分别记录干密度ρ1至ρn，在制样过程中，将温度传感器预先放置在试样中心。
7.2)、将所有试样中的温度传感器连接到采集仪，将试样在常温状态放入温度控制设备进行冻结，同时开始温度数据采集，采集间隔为1-5s。
8.3)、温度数据采集完毕将所有试样的温度数据进行处理，确定每个物理状态的冻结温度。构建了冻结温度tf随质量含水量ω呈如下函数关系的函数：
9.tf＝a+b*e-c*ω
ꢀꢀꢀꢀꢀꢀ
(1)。其中，a为第一拟合参数、b为第二拟合参数、c为第三拟合参数，且ω≥0，c》0。
10.取平均值
11.而参数c取为关于干密度的函数，作为干密度的函数进行冻结温度修正。其中，ai、bi分别为某一干密度ρi时拟合的冻结温度参数。
12.其中i为自然数(1、2
…
n)，n为自然数(1、2
…
n)。
13.通过获得的(ρ1，c1)、(ρ2，c2)、(ρ3，c3)至(ρn，cn)n个点绘制在直角坐标系中，发现参数c与干密度呈线性关系，从而建立起参数c与干密度的线性关系：
14.c(ρ)＝d+g*ρ
ꢀꢀꢀꢀꢀꢀ
(5)。
15.其中d为第四拟合常数、g为第五拟合常数。
16.从而可得不同干密度和不同含水量条件下，某种土的冻结温度预测模型为：
[0017][0018]
其中，
[0019][0020]
c(ρ)＝d+g*ρ。
[0021]
其优点在于：
[0022]
1、本发明提出了一种土体冻结温度的预测模型，综合考虑了含水量和干密度两个因素的影响。这两个因素是工程常规宏观参数，便于获取。
[0023]
2、本预测模型不需要对土体进行粒径含量和矿物组成等因素进行分析，仅需常规的两个物理参数即可预测，具有高效和便捷的优势。
[0024]
3、可基于监测所测土样的冻结过程温度时程图获得土体不同物理状态的冻结温度。
附图说明
[0025]
图1为土体降温曲线图。
[0026]
图2为相同干密度时冻结温度预测模型。
[0027]
图3为不同干密度时冻结温度预测模型。
[0028]
图4为c与干密度关系。
[0029]
图5为不同干密度和不同含水量冻结温度曲线图。
[0030]
图6为实施例中沈阳土体c与干密度关系图。
具体实施方式
[0031]
本发明专利的核心内容：
[0032]
1、构建了一种指数函数的冻结温度预测模型，即公式(1)所述模型，可以用来准确预测土体在不同物理状态下的冻结温度。
[0033]
2、本预测模型考虑了土体的含水量和干密度两个因素的影响(也可不考虑干密度的影响，即只做一种干密度不同含水量的预测)。对于未知的土体，仅需测量几个不同物理状态的冻结温度即可确定相关参数，从而准确地预测连续物理状态的冻结温度变化规律。
[0034]
3、对于熟悉的土体冻结温度，可以利用本模型快速得出不同物理状态冻结温度而不需要进行额外的试验，具有准确、高效的特点，降低了成本。
[0035]
类似专利方法对比：
[0036]
《一种测定土体冻结温度的试验装置》(专利号202010546463.3)、《高压土冻结温度测试装置》(201110218580.8)均是通过试验方法确定土体的冻结温度，且仅能确定所测土体某个物理状态下的冻结温度。但是，通过这两种方法确定所测土体几个物理状态的冻结温度后，可采用本发明专利内容进行其他物理状态的冻结温度预测。
[0037]
《非接触式冻结温度确定》(201010280914.x)是通过试验方法确定路面冰水混合物的冻结温度，不能用来确定土体的冻结温度，尤其是不能用来预测不同含水量和不同干密度条件下的土体冻结温度。
[0038]
本实施方法：
[0039]
当对于某土体的冻结温度没有任何了解时，可通过少量的降温冻结监测获得几个数据点，然后基于此已知冻结温度状态预测其他物理状态冻结温度。用到的测试物体包括小体积高精度温度传感器(一般为小体积热敏电阻，精度在0.01℃及以上，需要二级及以上水银温度计校准)、能按照一定频率自动记录的采集仪(可以实现按照一定频率自动记录的已知设备均可)、被测试物品和电脑等。具体过程如下：
[0040]
1、制备3组不同质量含水量的土样，记为ω1、ω2、ω3，将其按照目标干密度制备测试土样，三组试验干密度分别为ρ1、ρ2和ρ3，在制样过程中，将温度传感器预先放置在试样中心。
[0041]
2、将所有试样中的温度传感器连接到采集仪，采集仪连接到电脑，将试样在常温状态(正温)放入温度控制设备(已知设备)进行冻结，同时开始温度数据采集，采集间隔为1-5s。
[0042]
3、温控设备设置的温度要远低于冻结温度，比如将最终温度设置为-10～-20℃。温度数据采集完毕将所有试样的温度数据进行处理，确定每个物理状态的冻结温度。
[0043]
根据对不同干密度和不同含水量土样进行多次冻结过程温度监测发现，冻结温度随含水量的增长而增长，但是随着含水量的增大，增长速率逐渐降低，近似呈双曲线/抛物线形状。本发明中构建了冻结温度tf随质量含水量ω呈如下函数关系的函数：
[0044]
tf＝a+b*e-c*ω
ꢀꢀꢀꢀꢀꢀ
(1)。其中，a为第一拟合参数、b为第二拟合参数、c为第三拟合参数，且ω≥0，c》0。
[0045]
从函数图形可见，当含水量足够大时，冻结温度tf具有上限值a。但实际上含水量ω不能无限大，在此约定ω
sat
≥ω≥0(ω
sat
为饱和含水量)。当含水量ω接近为0时，冻结温度下限为a+b，但是对于近似0含水量的土因水分含量极小，冻结时几乎没有相变，因此考虑其冻结温度也没有实际意义。
[0046]
对于上述三组试样，含水量ω1≠ω2≠ω3，但是干密度ρ1、ρ2和ρ3可以相等，也可以不相等。下面分别进行讨论。
[0047]
1.当ρ1＝ρ2＝ρ3(ω1≠ω2≠ω3)。
[0048]
当干密度相同时，每组试样至少1个，即最少需要3个相同干密度的试样。那么所构建的预测模型仅能描述一种干密度条件下不同含水量的冻结温度变化规律，通过三个含水量和三个冻结温度通过数值方法求解如下三个未知数的方程：
[0049][0050]
其中e为自然对数的底数。
[0051]
数值拟合求解可得：
[0052]
tf＝a1+b1*e-c1*ω
ꢀꢀ
(3)。
[0053]
拟合结果如图2所示。fit为拟合。
[0054]
需要说明的是，最少为3个不同含水量的试样才能求出3个未知量。但是更多的试验结果能让a、b、c三个未知量的拟合更准确。
[0055]
2.当ρ1≠ρ2≠ρ3(ω1≠ω2≠ω3)。
[0056]
当试样含水量不同，干密度也不相同时，3组试样理论上需要9个试样进行测试(每个干密度为一组，每组3个不同含水量试样)，即每组干密度包括三个不同含水量的试验，通过数值求解可得三个不同干密度的冻结温度表达式(当然，也可以有n组干密度试样，n≥3)：
[0057]
tf＝a1+b1*e-c1*ω
，(4-1)对应密度为ρ1的三种情况。
[0058]
tf＝a2+b2*e-c2*ω
，(4-2)对应密度为ρ2的三种情况。
[0059]
tf＝a3+b3*e-c3*ω
，(4-3)对应密度为ρ3的三种情况。
[0060]
实测与拟合结果如图3所示。当超过3组以上干密度时，记为ρn。
[0061]
通过对比分析发现，对于同一种土在不同的含水量和干密度时，冻结温度模型拟合参数a和b变化较小，可认为取定值。
[0062]
近似地，取平均值而参数c变化较大，取为关于干密度的函数，即将通过参数c作为干密度的函数进行冻结温度修正。
[0063]
通过获得的(ρ1，c1)、(ρ2，c2)和(ρ3，c3)三个点绘制在直角坐标系中，发现参数c与干密度呈线性关系，如图4所示。从而建立起参数c与干密度的线性关系：
[0064]
c(ρ)＝d+g*ρ
ꢀꢀꢀꢀꢀꢀ
(5)。
[0065]
其中d为第四拟合常数、g为第五拟合常数。
[0066]
从而可得不同干密度和不同含水量条件下，某种土的冻结温度预测模型为：
[0067][0068]
其中，
[0069][0070]
c(ρ)＝d+g*ρ。
[0071]
模型评估：
[0072]
本模型预测值预测效果可通过以下四个参数进行评估，分别为均方根误差(rmse)、平均误差(ad)、平均绝对误差百分比(mape)和纳什效率系数(nse)，从而评估模型的预测能力。
[0073]
其定义分别如下：
[0074]
均方根误差(rmse)：
[0075]
平均误差(ad)：
[0076]
平均绝对误差百分比(mape):
[0077]
纳什效率系数(nse)：
[0078]
公式(7)、(8)、(9)和(10)中：n为数据数量，yj为试验测试的冻结温度值，为yj的平均值，为利用公式(3)或公式(6)计算的冻结温度预测值。
[0079]
均方根误差(rmse)越接近于0、平均误差(ad)越接近于0、平均绝对误差百分比(mape)越接近于0％、纳什效率系数(nse)越接近于1，其预测效果越好。
[0080]
案例参考：
[0081]
下面沈阳某地粉质黏土冻结温度分析为例。所测土体塑限18.5，液限31.3，塑性指数12.8。以1.4g/cm3、1.5g/cm3和1.6g/cm3三种干密度，15％-34.4％含水量(重量)所测的冻结温度为例进行模型构建分析。试验所测冻结温度如表1所示。
[0082]
表1冻结温度试验结果(℃)
[0083][0084]
根据公式(1)及表1试验结果，通过数值方法进行参数拟合，三个干密度冻结温度分别如下：
[0085]
tf＝-0.4518-2.5460*e-0.1944*ω
，r2＝0.998，ρ＝1.4g/cm3。
[0086]
tf＝-0.4557-2.5584*e-0.16836*ω
，r2＝0.998，ρ＝1.5g/cm3。
[0087]
tf＝-0.4583-2.5095*e-0.1458*ω
，r2＝0.999，ρ＝1.6g/cm3。
[0088]
r2为拟合优度。
[0089]
如表2所示，通过分析可以认为利用式(1)拟合的tf(ω)，在不同干密度条件下，应具有相同的a，b，近似地，取平均值，得到：
[0090]
表2预测模型极限值
[0091][0092]
得到图5不同干密度和不同含水量冻结温度曲线图
[0093]
而不同干密度通过不同的c值，改变了函数在[15,35](％)区段的曲率，即
[0094]
tf＝-0.4553-2.5380*e-c(ρ)*ω
ꢀꢀ
(11)。
[0095]
为了得到c(ρ)的表达式，绘制c-ρ的曲线图6：
[0096]
不难看出c-ρ近似呈线性关系，拟合得到：
[0097]
c＝-0.243ρ+0.534，r2＝0.997。
[0098]
从而可得此粉质黏土冻结温度预测模型为：
[0099]
tf＝-0.4553-2.5380*e
(0.243ρ-0.534)*ω
。