一种不依赖转台的微机电惯性测量单元标定补偿方法

1.本发明涉及微机电惯性测量领域，具体是一种不依赖转台的微机电惯性测量单元标定补偿方法。


背景技术：

2.微机电系统(mems,micro-electro-mechanical system)，是指尺寸在几毫米乃至更小的高科技装置。惯性测量单元(inertial measurement units，imu)通常包含三轴角速率陀螺仪和三轴加速度计，是测量角速度和加速度的装置。
3.mems-imu(微机电惯性测量单元)具有如下优点：尺寸小、重量轻、结构坚固、功耗低、启动快、成本低、可靠性高、维护性好、环境适应性强。但是，目前mems-imu的精度尚不及光学惯导等设备，由于惯性导航系统中采用积分运算,即便是微小的惯性器件测量误差，随着时间增长都会引起惯性导航姿态、速度和位置计算误差的不断积累。因此，通过测试和误差补偿手段提高现有惯性器件的实际使用精度具有非常重要的意义。
4.传统imu的标定通常由特殊的精密转台来完成，使用机械转台按照一组精确控制的姿态以已知的转动角速度控制imu。然而，用于标定的装置通常都非常昂贵，使得标定的成本甚至超出imu硬件的成本。基于转台的标定方法简单、精度高，但是成本也较高。而现有的误差标定方法通常只考虑系统误差，难以实际提高imu的解算精度。


技术实现要素：

5.本发明的目的是提供一种不依赖转台的微机电惯性测量单元误差建模及标定补偿方法，包括以下步骤：
6.1)确定待标定补偿的微机电惯性测量单元及其补偿参数；
7.所述微机电惯性测量单元的测量参数如下所示：
[0008][0009]
式中，分别表示三轴加速度计和陀螺仪输出的加速度和角速度测量值；a＝[a
x a
y az]
t
、ω＝[ω
x ω
y ωz]
t
分别表示加速度和角速度的真实值；分别表示三轴加速度计和三轴陀螺仪的轴间非正交误差；分别表示三轴加速度计和三轴陀螺仪的标度因数；ba＝[b
ax b
ay b
az
]
t
、bg＝[b
gx b
gy b
gz
]
t
分别表示三轴加速度计和三轴陀螺仪的零偏；na和ng表示微机电惯性测量单元的随机误差参数，符合高斯分布
ba＝[b
ax b
ay b
az
]
t
、bg＝[b
gx b
gy b
gz
]
t
表示陀螺仪的偏置，为随机游走，其导数为高斯分布，即其中
[0010]
2)对微机电惯性测量单元的系统误差进行标定，得到确定性系统误差参数；
[0011]
对微机电惯性测量单元的系统误差进行标定的步骤包括：
[0012]
2.1)采集微机电惯性测量单元数据，步骤如下：
[0013]
(1)将imu水平静止50秒；
[0014]
(2)转动imu到另一不同姿态的位置；
[0015]
(3)静止至少1秒钟；
[0016]
(4)连续进行(2)、(3)操作50次以上。
[0017]
2.2)基于微机电惯性测量单元采集数据对微机电惯性测量单元的系统误差进行标定的步骤包括：
[0018]
确定微机电惯性测量单元的随机误差参数的步骤包括：
[0019]
2.2.1)将微机电惯性测量单元分别置于m个不同位置；在微机电惯性测量单元置于第k个位置和第k+1个位置之间，计算三轴加速度计的平均测量值k＝1,2，
…
，m-1；
[0020]
2.2.2)建立代价函数，即：
[0021][0022]
式中，重力加速度||g||＝g0；参数；参数为三轴加速度计的平均测量值；
[0023]
2.2.3)利用levenberg-marquard优化算法最小化代价函数f(θacc)，得到加速度计非对齐误差标定参数向量θ
acc
；所述参数向量θ
acc
如下所示：
[0024]
θ
acc
＝[α
yz
,α
zy
,α
zx
,s
ax
,s
ay
,s
az
,b
ax
,b
ay
,b
az
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0025]
2.2.4)确定每个静止区间内重力矢量方向，其中，u
a,k-1
为利用归一化四元数表示的k-1个静止区间的重力矢量方向；
[0026]
第k个静止位置重力矢量方向u
g,k
如下所示：
[0027]ug,k
＝ψ[ωi,u
a,k-1
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0028]
式中，ψ表示任意角速度积分算法，u
g,k
表示使用角速度向量序列ωi，通过积分运算得到的第k个静止位置重力矢量方向；
[0029]
2.2.5)建立损失函数f(θ
gyro
)，即：
[0030][0031]
2.2.6)利用levenberg-marquardt优化算法最小化公式(5)，得到三轴陀螺仪轴间非对齐误差标定参数向量θ
gyro
，即：
[0032]
θ
gyro
＝[γ
yz
,γ
zy
,γ
xz
,γ
zx
,γ
xy
,γ
yx
,s
gx
,s
gy
,s
gz
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0033]
3)分析确定微机电惯性测量单元的随机误差参数；
[0034]
分析确定微机电惯性测量单元的随机误差项的步骤包括：
[0035]
3.1)采样微机电惯性测量单元在静止状态下ω(t)时间长度内的imu数据，其中，
采样数目为n，采样时间为τ0；
[0036]
3.2)将imu数据分为k个组，设定每个时间段的时长τ＝mτ0，m≤(n-1)/2为用于平均的因子；
[0037]
三轴陀螺仪数据分组情况如下：
[0038][0039]
式中，ωi为陀螺仪的采样时间i处的输出；
[0040]
3.3)将imu数据按照时间段进行平均；每组三轴陀螺仪数据的平均值如下所示：
[0041][0042]
3.4)计算在每一平均时间τm平均值对应的方差并建立allan标准差σa(τm)随平均时间τm变化的双对数曲线，即allan方差曲线；
[0043]
3.5)对allan方差曲线进行曲线拟合，得到不同斜率下的随机误差项。
[0044]
所述随机误差项包括量化噪声、角度随机游走值、零偏稳定性、角速率随机游走值、速率斜坡。
[0045]
4)根据系统误差参数和随机误差参数，结合单目相机实时在线估计微机电惯性测量单元的零偏。
[0046]
实时在线估计微机电惯性测量单元的偏置的步骤包括：
[0047]
4.1)利用标定得到的确定性系统误差参数得到校正后的微机电惯性测量单元测量数据，如下所示：
[0048][0049]
4.2)结合单目相机和微机电惯性测量单元，建立联合优化代价函数：
[0050][0051]
其中，滑动窗口中的完整状态向量如下所示:
[0052][0053]
式中，xk是捕获第k图像时的imu状态包括imu在世界坐标系w中的位置速度和方向以及在imu机体坐标系中的加速度计偏置ba和陀螺仪偏置bg；n是关键帧的总数；m是滑动窗口中的特征总数，λ
l
是第一次观测到第l个特征的逆深度；bi表示第i个视觉关键帧处的载体系，ci表示第i视觉关键帧处的相机坐标系，w表示世界坐标系，fj表示第j个
特征点的坐标，表示ci对fj的观测，q
bc
表示相机坐标系和机体系之间的旋转四元数，p
bc
表示相机坐标系和机体系之间的平移向量；
[0054]
huber范数ρ(
·
)如下所示：
[0055][0056]
4.3)利用标定得到的随机误差参数，构建噪声项的对角协方差矩阵，如下所示：
[0057][0058]
4.4)利用levenberg-marquardt优化算法求解优化目标(10)的最小值，得到微机电惯性测量单元的实时零偏，进而得到微机电惯性测量单元准确位姿估计结果。
[0059]
值得说明的是，本发明提出了一种全面测试和补偿惯性测量单元误差的方法，该方法不需要使用专门测试标定设备。通过建立mems-imu的误差模型，使用优化方法标定误差模型中的确定性参数；使用allan方差分析方法确定随机误差参数；基于上述标定结果，采用与单目相机融合的非线性优化方法在线实时补偿零偏，最终达到提高导航定位精度的目的。通过实验分析，上述组合方法能够有效补偿低成本微机电惯性测量单元的误差，提高定位精度。
[0060]
本发明的技术效果是毋庸置疑的，本发明通过建立误差模型，在不依赖价格高昂测试标定设备情况下，采用多种不同的组合测试和误差补偿手段，提高mems-imu实际使用精度。
[0061]
本发明在利用特定方法采集数据后，使用非线性优化方法实现误差模型中确定性系统误差参数的标定。
[0062]
本发明使用allan方差分析方法获得mems-imu的随机误差参数，主要可以得到具有使用价值的角度随机游走系数和零偏不稳定性系数。
[0063]
本发明基于视觉和imu融合的非线性优化方法，在确定系统误差和随机误差系数基础上，有效在线实时估计imu的偏置，提高imu导航解定位精度。
附图说明
[0064]
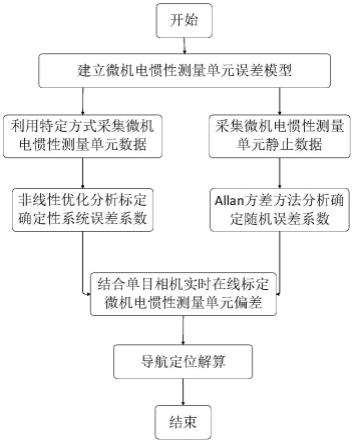
图1为本发明方法的实施流程图；
[0065]
图2为bmi055型mems-imu误差标定采集加速度计数据；
[0066]
图3为静止区间检测结果；
[0067]
图4为bmi055型mems-imu水平静止时的陀螺仪读数；
[0068]
图5为bmi055陀螺仪的allan方差曲线；
[0069]
图6为bmi055加速度计的allan方差曲线；
[0070]
图7为单目视觉和惯性融合示意图；
[0071]
图8为加速度计零偏实时估计结果；
[0072]
图9为陀螺仪零偏实时估计结果；
[0073]
图10为三维定位结果比较；
[0074]
图11为三个坐标轴上的定位结果比较。
具体实施方式
[0075]
下面结合实施例对本发明作进一步说明，但不应该理解为本发明上述主题范围仅限于下述实施例。在不脱离本发明上述技术思想的情况下，根据本领域普通技术知识和惯用手段，做出各种替换和变更，均应包括在本发明的保护范围内。
[0076]
实施例1：
[0077]
实施例1的具体实施流程如图1所示，包括以下步骤：
[0078]
1)mems-imu误差建模
[0079]
imu的误差可以分为系统误差和随机误差。系统误差可以事先标定确定，随机误差可以直观的理解为零偏的波动和漂移程度，通常假设零偏噪声服从高斯分布。imu误差包括陀螺仪的误差和加速度计的误差，陀螺仪与加速度计的误差特性类似，仅是测量的物理量含义不同。
[0080]
完整的mems-imu传感器模型为：
[0081][0082]
式中，分别表示三轴加速度计和陀螺仪输出的加速度和角速度测量值；a＝[a
x a
y az]
t
，ω＝[ω
x ω
y ωz]
t
表示加速度和角速度的真实值；表示加速度计和陀螺仪的轴间非正交误差；表示角速度计和陀螺仪的标度因数；ba＝[b
ax b
ay b
az
]
t
，bg＝[b
gx b
gy b
gz
]
t
表示加速度计和陀螺仪的零偏；na和ng分别表示加速度计和陀螺仪的随机误差项。
[0083]
对于imu随机误差，具体包括：
[0084]
a)量化噪声，这是数字传感器必然出现的噪声，由于ad采集把连续时间信号采集成离散信号过程中的精度损失。
[0085]
b)速度(角度)随机游走，加速度计加速度并输出时是有噪声的，这个噪声里面的白噪声。
[0086]
c)角速率(加速度)随机游走，角速率里面并不全是白噪声，还有马尔可夫性质的误差成分，而这个误差是角加速率白噪声累积的结果。
[0087]
d)零偏不稳定性噪声，imu常用该指标来体现精度，把它理解为零偏随时间的缓慢变化。
[0088]
e)速率斜坡，是趋势性误差，最常见的原因是温度引起零位变化。
[0089]
f)零偏重复性，是指imu断电之后重新上电时，它当前的零偏并不与断电之前的零偏一致。
[0090]
对于低成本的mems-imu，在对随机误差进行分析时，实际上难以得到上述每种典型误差系数，主要有用的是角度随机游走系数和零偏不稳定性系数。bmi055是一个测量六自由度运动和旋转的mems-imu,包括三轴加速度传感器和三轴陀螺仪，尺寸只有3
×
4.5毫米，广泛应用于消费级无人机、智能手机以及智能穿戴设备中。
[0091]
2)采用非线性优化方法的确定性系统误差优化标定
[0092]
假定imu载体上，存在理想正交坐标系轴间非正交误差则是由于三轴加速计坐标系陀螺仪坐标系的封装误差和轴到轴之间的对齐误差造成。
[0093]
在基于转台的标定方法里，imu的坐标系规定为与转台的坐标系重合，这样转台的输入，才能成为imu测量的真实值。当不使用转台进行标定时，坐标系可以人为规定，基于此，可以对误差模型进行简化。令坐标系的xb轴与加速度计的xa轴重合，且xboyb与xaoya共面。
[0094]
在这样的假设下，加速度计的轴间非正交误差简化为：
[0095][0096]
为了标定加速度计非对齐误差，需要估计如下的参数向量：
[0097]
θ
acc
＝[α
yz
,α
zy
,α
zx
,s
ax
,s
ay
,s
az
,b
ax
,b
ay
,b
az
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0098]
将mems-imu静置在m个可以区分的，短时间内稳定的位置。在不同静置位置之间，以较为稳定的速度旋转移动mems-imu。于是，在每一个静止区间内，通过平均加速度计的读数，可以提取在非对齐的坐标系中m个加速度向量由于对每一个静止区间信号进行了平均，所以忽略测量噪声，由式(1)推导定义如下的函数：
[0099][0100]
当imu位于静止区间时，输入只有重力加速度||g||＝g0，定义代价函数：
[0101][0102]
采用levenberg-marquardt(lm)优化算法最小化代价函数f(θ
acc
)得到θ
acc
。
[0103]
将θ
acc
作为已知量，进一步标定陀螺仪的轴间非正交误差，所需标定的陀螺仪参数为：
[0104]
θ
gyro
＝[γ
yz
,γ
zy
,γ
xz
,γ
zx
,γ
xy
,γ
yx
,s
gx
,s
gy
,s
gz
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0105]
将静止的imu陀螺仪信号进行平均即可得到陀螺仪的零偏，因此这里假设陀螺仪的输出是无偏的。通过标定后的加速度计输出，就可以确定每个静止区间内重力矢量方向，令u
a,k-1
为利用归一化四元数表示的k-1个静止区间的重力矢量方向。
[0106]
定义操作符ψ，通过使用k-1个静止位置到k个静止位置之间的角速度ωi可以得到：
[0107]ug,k
＝ψ[ωi,u
a,k-1
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0108]
式中，ψ表示任意角速度积分算法，u
g,k
表示使用角速度向量序列ωi，通过积分运算得到的第k个静止位置重力矢量方向。因此，定义损失函数：
[0109][0110]
采用levenberg-marquardt(lm)优化算法最小化公式(8)得到θ
gyro
。
[0111]
针对bmi055型mems-imu，采取如下操作，采集得到标定所需数据。
[0112]
(1)将imu水平静止50秒；
[0113]
(2)转动imu到另一不同姿态的位置；
[0114]
(3)静止至少1秒钟；
[0115]
(4)连续进行(2)、(3)操作50次以上。
[0116]
得到的传感器加速度计数据如图2所示，并对其中的静止区间进行了识别，如图3所示。
[0117]
经算法标定后得到的误差模型参数为：
[0118][0119][0120]bg
＝[-2.39227e-05
ꢀ‑
2.03875e-05 1.73784e-06]
t
，ba＝[0.0148413 0.120341
ꢀ‑
0.0155797]
t
[0121]
在后续实验过程中，利用上述系数进行校正运算。
[0122]
3)基于allan方差的随机误差系数分析
[0123]
allan方差的物理意义以及应用本质来源于它与功率谱之间的关系。allan方差法是一种时域分析技术，对实际静态条件下采集的惯性器件数据进行分析得到双对数曲线图，根据不同拟合直线的斜率可以辨识不同的误差系数。allan方差对mems-imu误差模型进行分析的方法可以总结如下：
[0124]
(1)保持imu传感器静止获取时间长度为ω(t)的imu数据，采样数目为n个点，采样时间为τ0，如图4所示，是bmi055传感器静止平放时陀螺仪的读数。
[0125]
(2)将数据进行分为k个组，设定每个时间段的时长τ＝mτ0，此处m为用于平均的因子，m可以取为满足m≤(n-1)/2的任意值。其中，连续的数据组中间间隔了时间τ0。以陀螺仪为例，ωi为陀螺仪的采样时间i处的输出，则数据分组情况如下：
[0126][0127]
(3)将传感器数据按照时间段进行平均。以陀螺仪为例，可以采用基于角速率测量值和基于角度测量值的方法。基于角速率测量值的方法中：每一组的持续时间τ称为相关时间，每一组的平均值计算如下：
[0128][0129]
(4)这样，就会得到m个在每一平均时间τm对应的方差根据这m个点作图，可得到allan标准差σa(τm)随平均时间τm变化的双对数曲线，即allan方差曲线，对bmi055型mems-imu绘制得到的allan方差曲线如图5和图6所示。
[0130]
通过曲线拟合，可以得到不同斜率下的误差项。量化噪声，在斜率为m＝-1，处可以读出；角度随机游走斜率为m＝-0.5，τm＝1处可以读出；零偏稳定性为底部的平坦区读出的常值；角速率随机游走在斜率为m＝0.5，τm＝3处可以读出；速率斜坡在斜率为m＝1，处可以读出。
[0131]
allan方差可用于分析五种典型误差，但是低成本mems-imu中并不是五种误差都有表现，具体的拟合参数见表1。
[0132]
表1 bmi005 imu allan方差估计参数
[0133][0134]
通过allan方差分析，理想情况下可以得到器件的量化噪声、角度随机游走、角速率随机游走、零偏不稳定性噪声、速率斜坡，这些都是对零偏质量的分析，也可以直观的理解为零偏的波动和漂移程度，但是并没有分析零偏本身的大小，而这正是要去估计的误差。而系统误差的标定过程中，需要在静基座下进行采集数据，在动基座下采集的数据，受基座运动特性影响；此外，imu每次上电时候的偏差不同，偏差还与温度相关，因此，只有在线估计补偿才能够满足导航精度和实时性的要求。
[0135]
4)基于单目视觉和惯性融合非线性优化的在线mems-imu误差估计
[0136]
随着智能手机、机器人导航、自主驾驶、虚拟现实(vr)和增强现实(ar)等的广泛应用，基于视觉传感器和imu的天然互补性，已经成为充分自我感知和环境感知的最小传感器组合。如果把工作环境限定在静态、刚体、光照变化不明显、没有人为干扰的场景，以相机为
主要传感器的视觉同时定位与地图构建(simultaneous localization and mapping，slam)技术，即在没有环境先验信息的情况下，于运动过程中建立环境的模型，同时估计自己的运动，已经相当成熟。整体上,视觉和imu传感器联合实现载体的位姿估计，存在一定互补性质，imu适合计算短时间、快速的运动；视觉适合计算长时间、慢速的运动。因此，可利用视觉定位信息来估计imu的零偏,减少imu由零偏导致的发散和累积误差。在实际应用中，将imu建模为：
[0137][0138]
式中，上标g表示陀螺仪,a表示加速度计,w表示在世界坐标系，b表示imu坐标系，ω,a为imu的真实值为,为测量值，q
bw
为世界坐标系到imu坐标系的变换四元数。ng(na)表示陀螺仪(加速度计)的角度(速度)随机游走误差，假设符合高斯分布bg，ba表示陀螺仪的偏置，建模为随机游走，其导数为高斯分布，即其中
[0139]
基于视觉和imu融合的示意图见图7。视觉和imu的融合，一般采用滑动窗口的方式，构建优化问题：
[0140][0141]
式中，滑动窗口中的完整状态向量定义为:
[0142][0143]
其中，xk是捕获第k图像时的imu状态包括imu在世界坐标系w中的位置速度和方向以及在imu机体坐标系中的加速度计偏置ba和陀螺仪偏置bg。n是关键帧的总数，m是滑动窗口中的特征总数，λ
l
是第一次观测到第l个特征的逆深度。bi表示第i个视觉关键帧处的载体系，ci表示第i视觉关键帧处的相机坐标系，w表示世界坐标系，fj表示第j个特征点的坐标，表示ci对fj的观测，q
bc
表示相机坐标系和机体系之间的旋转四元数，p
bc
表示相机坐标系和机体系之间的平移向量。ρ(
·
)为huber范数，定义如下：
[0144][0145]
采用levenberg-marquardt(lm)优化算法求解式(12)的最小二乘问题，即可得到imu的实时偏差。基于bmi055型imu，结合matrixvision mvbluefox-mlc200w型摄像头，采用表1中估计结果，手持imu和摄像头的组合，在小范围内运动，实验得到图8和图9的imu偏差实时估计结果。在实验开始的阶段偏差的波动是由于imu和视觉融合初始化的结果，在系统完成初始化之后，imu的偏差趋于稳定。在imu偏差估计基础上的定位结果如图10和图11所示。可以看到，相比单纯使用imu进行定位，imu与视觉融合定位减小了位置的发散，定位结
果更加接近真实的运动轨迹。该方法的问题在于算法复杂度较高，对于实验运行环境有一定要求，需要实验环境满足静态、刚体、光照变化不明显、没有人为干扰的场景等条件。