一种新型确定含水层热物性参数的微热试验方法

1.发明涉及一种新型确定含水层热物性参数的微热试验方法，属于微热试验技术领域。


背景技术：

2.开发利用绿色可再生的浅层地热能不仅可以有效缓解能源紧张问题，更能大大减少环境污染，是我国目前势在必行的研究项目。在开发地热能的初期，需要对地热资源进行相关评价，评价内容包括浅层地热资源总容量、可开采资源量以及地层热量补给速率等等，而这些均与区域水文地质条件、含水层和岩土体的热物性密切相关。热物性中最为重要的参数是含水层、岩土体导热系数和比热容，其大小反映了含水层、岩土体的蓄热、导热能力和传热效率，在工程应用中，选择较大导热系数的含水层和岩土体进行开发利用往往可以有效提高热源的利用率，降低投资成本。因此对含水层和岩土体导热系数进行充分的研究和评估是十分必要的。
3.此外，含水层和岩土体的传热问题在地热资源的开发与利用中是一个十分重要的研究方向，其中有效导热系数作为表征含水层热运移的重要参数有着举足轻重的地位，其意义在于将包括对流弥散、传导作用在内的热量运移过程用有效导热系数这样一个参数来表示。采用一定方法精准确定含水层和岩土体的导热系数具有重要的理论意义和实际工程价值。
4.目前测试导热系数的方法通常是现场热响应试验，试验的原理是通过给与含水层(岩土体)一定热源，观测热量的运移分布从而推导出含水层和岩土体的导热系数，该类试验周期长，操作较为复杂。


技术实现要素：

5.本发明基于热径向对流弥散理论研究之上，提出了一种新型确定含水层热物性参数的微热试验方法，具有试验周期短，操作简易，数据处理直观等优点，具有很好的推广应用价值。
6.为解决上述技术问题，发明所采用的技术方案如下：
7.一种新型确定含水层热物性参数的微热试验方法，包括如下步骤：
8.1)以热径向对流弥散理论研究为基础，依据热量守恒原理建立微热试验的理论模型，通过数学变换，建立理论模型不同渗流条件、不同参数条件下的标准曲线；
9.2)通过微热试验，进行不同渗流条件和不同激发强度下的微热试验，通过传感器获取实测数据，绘制实测数据曲线；
10.3)采用配线法将标准曲线与微热试验实测数据曲线进行匹配，记录对应的坐标值，通过计算得到含水层导热系数，通过相关公式推导得到岩土体导热系数、含水层热弥散度等其余热物性参数。
11.上述利用微热试验获取实测数据，绘制实测数据曲线，具有试验周期短、试验简
单，结果精确等特点。
12.上述步骤1)中，根据微热试验理论得到的半解析解绘制无量纲温度变化t
*d
和无量纲时间τ的标准曲线；步骤2)中，根据采集到的井孔内温度变化值t与时间t的观测数据，绘制与标准曲线相同模数的温度变化t与时间t的实测曲线图，温度变化值t和时间t均取对数；步骤3)中，使实测曲线坐标原点与标准曲线坐标原点在坐标图层的同一高度，通过平移实测曲线时间坐标轴t来匹配实测曲线与标准曲线，记录拟合标准曲线的α值，无量纲时间τ值，时间t值。
13.上述步骤1)中，微热试验的理论模型，建立在热径向对流弥散理论研究之上，依据热量守恒原理建立的一维条件下，不考虑z方向上热量运移的理论公式，通过拉普拉斯变化及逆变换对理论公式进行求解，选用stehfest算法和talbot算法建立理论模型不同渗流条件、不同参数条件下的标准曲线。
14.上述步骤1)中，综合利用matlab和grapher绘图软件，绘制不考虑流速和考虑流速两种情况下无量纲温度变化t
*d
与无量纲时间τ关于α(水热容量与含水层热容量比值)参量的标准曲线，即前述选用stehfest算法建立的不考虑流速情况标准曲线和talbot算法建立的考虑流速情况标准曲线。
15.上述步骤1)中，微热试验的理论模型需要通过以下方程和定律建立：径向流下考虑热机械弥散项的热量运移方程；根据热量守恒定律，井管内热量的变化与流过含水层r＝rw处的热量相等，建立热量平衡方程；
16.径向流下，考虑热对流弥散项的热量运移方程：
[0017][0018]
根据热量守恒定律，井管内热量的变化与含水层r＝rw处的热量相等：
[0019][0020]
初始条件
[0021]
t(r,t)|
t＝0
＝0,r》rwꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0022]
t
*
(0)＝t0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0023]
边界条件
[0024]
t(r,t)|r→
∞
＝0,t》0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0025]
t
*
(t)＝t(rw,t),t》0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0026]
以上式中：t为温度，t(rw,t)为t时刻井管壁处的温度变化值，t(r,t)表示含水层中距井中心为r时t任意时刻的温度的变化值，t
*
(t)为t时刻井孔内的温度变化值，r为含水层内某点到井中心的距离，rw为井管半径，rs为井管内导热管的半径；t为时间；λ(r)为含水层的有效导热系数；(ρc)f为地下水热容量，(ρc)
fs
为含水层的热容量；t0为初始温度变化值；为地下水实际流速，b为含水层厚度，q为注水流量,θ为含水层孔隙度；
[0027]
当u＝0时，即含水层不考虑水流流动时，式(1)变成如下形式，即热的传导方程：
[0028]
[0029]
式(1)至式(6)数学模型的方程形式比较复杂，且因公式(1)和(7)表达式不同，需将公式(1)方程分成考虑流速和不考虑流速两种条件的情况，分别计算，总体思路是采用拉普拉斯变换的方法对其进行求解，将上述方程、定解条件等通过无量纲因子和参变量转换为无量纲形式，依次对其进行拉普拉斯变换；
[0030]
(1)不考虑流速情况下的理论模型求解：
[0031]
通过无量纲变换将式(7)转换为如下形式：
[0032][0033]
其中δw＝1，
[0034]
再依次对式(2)-(6)做无量纲变化得：
[0035][0036]
td(δ,0)＝0,0《δ《∞,τ＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0037]
t
*d
(0)＝td,δ＝1,τ＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0038]
td(δ,τ)＝0,δ
→
∞,τ》0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0039]
t
*d
(τ)＝td(δ,τ),δ＝1,τ》0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0040]
最后对式(8)τ做拉普拉斯变换，式(8)热传导方程转化为:
[0041][0042]
井管内热量的变化与流过含水层r＝rw处的热量相等，该式转化为
[0043][0044]
定解条件：
[0045][0046][0047][0048]
上述拉普拉斯转换式中：
[0049]
为t
*d
的拉氏变换的象函数，为td的拉氏变换的象函数，t
*d
为井孔中温度变化比值，为含水层中温度变化比值，为距井中心距离与井半径的比，井内导热管半径与井半径的比，δw＝1，p为拉氏变换复变量，无量纲时间，无量纲时间，为与含水层固有性质相关的无量纲参数，为水的热容量与含水层的热容量的比。
[0050]
根据n阶修正贝塞尔方程：
[0051][0052]
通解为：
[0053]
y＝c1kn(βx)+c2in(βx)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(20)
[0054]
其中：in(x)和kn(x)分别为第一类和第二类修正贝塞尔函数；
[0055]
当n＝0时，
[0056]
式(14)的解为：
[0057][0058]
根据式(17)知：
[0059][0060]
又因为第一类修正贝塞尔函数i0(x)为指数增长型函数，具有性质：当x
→
∞时i0(x)
→
∞，因此c2＝0，所以，
[0061][0062]
又根据0阶修正贝塞尔函数的性质知：
[0063][0064][0065]
将式(22)代入式(15)和(18)中可得：
[0066][0067]
由(18)可得：
[0068][0069]
由此可以得到当含水层处于静止条件下，流速u＝0时该理论模型在laplace空间的解析解为：
[0070][0071][0072]
公式(26)即为在不考虑流速情况下的拉普拉斯变换域中所得出的最终解，但是想要在实际实验中运用此解，还需要对公式(26)进行拉普拉斯逆变换，在拉普拉斯数值反演方法中，stehfest(1970)方法以简单易行、计算时间短等优点被广泛应用：
[0073][0074]
其中：f(t)为实空间的像原函数；f(s)为拉氏空间的像函数；n为求和项数；
[0075]
将公式(26)代入公式(27)中进行拉普拉斯逆变换得：
[0076][0077]
综上可得：
[0078]
t
*d
＝f(α,γ,τ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
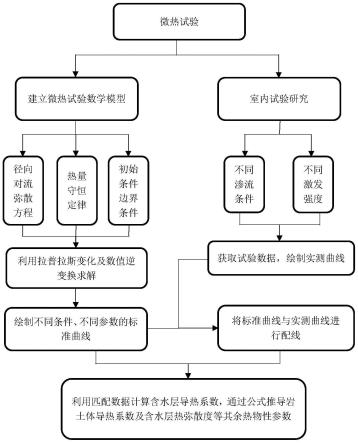
(29)
[0079]
由此可知，在不考虑流速情况下微热试验的理论模型中，控制测试井中无量纲温度变化t
*d
的无因次参数共3个，其中为水的热容量和含水层的热容量之比，反映了含水层相对于水的储热能量强弱，为与含水层热容量相关的参数，δs反映了井管内导热管半径大小和井孔半径大小的比值，在假设条件中，将忽略导热管和井孔间的空隙，所以δs为1，τ为无因次时间，由此可利用matlab软件绘制关于α参量的无量纲温度变化随时间变化标准曲线；
[0080]
(2)考虑流速情况下的理论模型求解：
[0081]
通过无量纲变换可将式(1)转换成如下形式：
[0082][0083]
对无量纲因子τ做laplace变换可得：
[0084][0085]
式中：β为与含水层导热系数和试验过程中试验孔流量相关的参数，若在流量和孔隙度等变量固定的条件下，含水层的导热系数λ为定值，β为常数，而在研究含水层热量运移问题的过程中，水流对温度场的影响不可忽略；
[0086]
又因为对比n阶修正贝塞尔方程和式(31)，不可以直接套用，需对式(31)做如下变换，为方便书写和理解，令x＝δ，则式(31)变换为：
[0087]
xy
″
+βy
′‑
pxy＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(32)
[0088]
设：y＝x-m
·
u，则：
[0089]y′
＝x-mu′‑
mx-m-1uꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(33)
[0090]y″
＝x-mu″‑
2mx-m-1u′
+m(m+1)x-m-2uꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0091]
将式(33)和(34)代入(32)得：
[0092][0093]
根据n阶修正贝塞尔方程的解，可得：
[0094]
[0095][0096]
由此可得，当n＝0时，
[0097][0098]
同样根据定解条件以及第一类修正贝塞尔函数i0(x)具有如下性质：当x
→
∞时i0(x)
→
∞，可得到c2＝0。
[0099][0100]
再将式(39)和式(18)代入无量纲化后的热量守恒条件即式(15)，得：
[0101][0102][0103]
由此可以得到当含水层在考虑流速情况下，微热试验理论模型在laplace空间的解析解为：
[0104][0105][0106]
和不考虑流速情况下求解过程相同，采用精度更高，考虑了复变域的talbot方法进行laplace逆变换：
[0107][0108]
其中，f(t)为实空间的像原函数；f(p)为拉氏空间的像函数，p＝2n/5t；s(θ)＝pθ(cotθ+i)；σ(θ)＝θ+(θcotθ-1)cotθ
[0109]
将公式(43)代入公式(44)中进行拉普拉斯逆变换，综上可得：
[0110]
t
*d
＝f(α,β,γ,τ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(45)
[0111]
其中，为水的热容量和含水层的热容量之比，为与含水层导热系数和试验过程中试验孔流量相关的参数，为与α相关的参数，为无量纲时间。
[0112]
由此可以得到在考虑流速情况下的微热试验理论中，控制测试井中无量纲温度变化的无因次参数共4个；与不考虑流速情况下一致，α指的是水的热容量和含水层的热容量之比，反映了含水层相对于水的储热能量强弱，β的大小与注入含水层内部的水流量以及含水层的性质相关，且反映了热量在含水层的运移过程中随着水流量的增加，对流弥散作用
明显增强，远远大于分子扩散；
[0113]
再次对β进行分析：
[0114][0115]
其中，为热扩散率，反映了含水层的导热速率的快慢，为水的热容量和含水层的热容量之比；根据β的表达式可以看出，β的大小与含水层的导热系数息息相关，在考虑流速情况下含水层的导热系数与流速、介质的孔隙度以及渗透系数有关，且0《β《1；γ与参数α和δs密切相关，除了反映含水层本身的热物性外，还反映了微热试验中导热管半径大小对试验结果的影响，τ为无因次时间；由此可固定其他参数值，利用matlab软件绘制关于α、β参量的无量纲温度变化随时间变化的标准曲线；
[0116]
热对流弥散模型中含水层的有效导热系数λ是由滞止导热系数λ
*
和热机械弥散系数λv两部分组成；由此，含水层中有效导热系数λ可表示为：
[0117]
λ＝λ
*
+λvꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(46)
[0118]
含水层滞止导热系数λ
*
指的是地下水不流动时的含水层导热系数，属含水层(包含含水层骨架和地下水)自身的热物理参数，与地下水流速、流量等因素无关，即在不考虑流速情况下的所需求解的参数，此时热的传递方式只有传导作用，同样含水层的滞止导热系数可由下式计算：
[0119][0120]
式中：θ为含水层孔隙度，λs为岩土体导热系数，(ρc)
fs
＝θ(ρc)f+(1-θ)(ρc)s，(ρc)f和(ρc)s分别为水和固体骨架的热容量；可以通过不考虑流速情况下的微热试验求出含水层的滞止导热系数和含水层的热容量，从而可以利用式(47)反推出岩土体的导热系数；
[0121]
热机械弥散系数λv则与含水层的流速密不可分，在孔隙含水层热量运移相关研究中某些学者认为纵向热机械弥散系数λv与流速u成正比，因此可表示为：
[0122]
λv＝a
x
(ρc)fu
ꢀꢀꢀꢀꢀꢀꢀꢀ
(48)
[0123]
式中：a
x
为纵向弥散度；u为地下水实际流速，(ρc)f为水的热容量，热弥散系数从定义上看指的是单位温度梯度下通过单位多孔介质截面的热量，其大小展现了多孔介质通过热弥散作用传递热量的能力强弱。
[0124]
上述步骤2)中，微热试验是通过瞬间增加或减少井孔内的温度，记录井孔内温度随时间变化，研究其温度变化规律，进而求取含水层的热物性参数。
[0125]
进一步优选，步骤2)中，在室内承压含水层试验平台或现场试验井孔中进行微热试验，根据微热试验方法，先后获得两种不同流速情况下、温差比和试验时间t试验数据，在grapher绘图软件中绘制关系实测曲线。
[0126]
上述步骤3)中，求取含水层导热系数并通过公式推导其余热物性参数的步骤如下：
①
在grapher软件中将不考虑流速和考虑流速情况下的实测曲线分别和相应条件下的标准曲线对应，置于同样模数的双对数坐标下，固定纵坐标在同一高度对横坐标进行平移，
直至两曲线重合；
②
任取一匹配点，记录下匹配点的对应坐标值：[t]，[τ]，[α]，其中，考虑流速情况下，还需要记录下对应标准曲线的值：[β]。已知水的热容量(ρc)f与井管半径rw，根据不考虑流速情况下标准曲线依据求出含水层的滞止导热系数根据考虑流速情况下标准曲线依据可以求出含水层的有效导热系数λ，依据λv＝λ-λ
*
可以求出含水层的热机械弥散系数λv，依据求出热弥散度a
x
。同时，依据求出含水层的热容量(ρc)
fs
。此外，根据室内土工试验资料可已知孔隙度θ，同时，在求出含水层的热容量(ρc)
fs
基础上，根据(ρc)
fs
＝θ(ρc)f+(1-θ)(ρc)s可求出岩土体固体骨架热容量(ρc)s，依据求出岩土体导热系数λs。
[0127]
上述方法，具有试验周期短、操作简单的优点；理论模型通过严格的数学推导得到，理论严谨，采用配线法确定含水层热物性参数，方法简单易掌握。
[0128]
本发明未提及的技术均参照现有技术。
[0129]
有益效果：与现有方法相比，本发明所提供的一种新型确定含水层热物性参数的微热试验方法，具有以下优点：
[0130]
(1)本发明提出的微热试验理论公式基于热径向对流弥散理论研究之上，通过严格的数学推导，理论严谨，并结合室内试验进行了验证；
[0131]
(2)热物性参数的确定采用配线法，方法简单，易于掌握；
[0132]
(3)相较于传统的确定热物性参数的方法，微热试验试验周期短，操作方法简单，不仅可以得到含水层的有效导热系数、滞止导热系数、热机械弥散系数、热弥散度和热容量，也可以反推得到岩土体的导热系数，且准确性高，具有很好的推广价值。
附图说明
[0133]
图1为本发明方法的操作流程图；
[0134]
图2为根据微热试验理论，不考虑流速情况下，采用stehfest算法得到的无量纲温度变化t
*d
和无量纲时间τ的标准曲线，即t
*d
－τ关系曲线；
[0135]
图3为根据微热试验理论，在考虑流速情况下，采用talbot算法得到的无量纲温度变化t
*d
和无量纲时间τ的标准曲线，即t
*d
－τ关系曲线；
[0136]
图4为室内半圆柱形砂槽承压含水层试验平台主视图；
[0137]
图5为室内半圆柱形砂槽承压含水层试验平台平面图；
[0138]
图6为室内半圆柱形砂槽承压含水层试验平台aa’方向剖面图；
[0139]
图7为室内半圆柱形砂槽承压含水层试验平台整体框架外观；
[0140]
图8为微热试验不考虑流速情况下，试验编号为w65℃1时主孔试验数据采用微热试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0141]
图9为微热实验不考虑流速情况下，试验编号为w75℃1时主孔试验数据采用微热试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0142]
图10为微热实验不考虑流速情况下，试验编号为w85℃1时主孔试验数据采用微热
试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0143]
图11为微热试验在考虑流速情况下，试验编号为y(
△
h＝6)45℃1主孔试验数据采用微热试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0144]
图12为微热试验在考虑流速情况下，试验编号为y(
△
h＝9)65℃1时主孔试验数据采用微热试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0145]
图13为微热试验在考虑流速情况下，试验编号为y(
△
h＝12)85℃2时主孔试验数据采用微热试验方法进行线状热源激发获取主孔温度变化数据确定含水层热物性参数时的配线图；
[0146]
图中，1为试验平台主井孔，2为径向布置的1-5号温度传感器，3为承压含水层，4为试验平台过滤层，5为试验平台外侧挡板，6为试验平台排水口，7为试验平台水位观测孔，8为试验平台9根测压管，9为计算机数据收集系统，10为隔水顶板与隔热层，11为沙袋，12为微热试验激发装置，13为隔水底板与隔热层，14为试验平台溢水口。
具体实施方式
[0147]
为了更好地理解发明，下面结合实施例进一步阐明发明的内容，但发明的内容不仅仅局限于下面的实施例。
[0148]
利用微热试验确定含水层热物性参数，首先在室内进行微热试验，如图4-图7所示，采用选定的多孔砂样介质装填的半圆柱形砂槽模拟承压含水层系统，系统由模型框架、承压含水层、温度观测装置构成。模型框架整体设计为高2.2m、半径2m的半圆柱状钢架，侧面和底面设置支撑架，预留排水孔和各观测孔外伸接口，在半圆柱圆弧侧边距底板1.5m处预留四个溢水孔以满足定水头要求。承压含水层模拟承压环境，厚0.75m，介质为0.25mm-0.50mm的中细砂，承压含水层的顶、底板铺设塑料膜和隔热膜进行防水隔热处理，顶板上铺设砂袋施加压力，承压含水层由侧边进水，底部排水。温度观测装置预置在主孔及主孔周围一定距离处，通过电缆与计算机相连进行数据传输。微热试验激发装置的结构及使用，参照本技术人同期申请的专利申请：一种确定含水层热物性参数的微热试验装置及方法。
[0149]
如图1所示，一种新型确定含水层热物性参数的微热试验方法，包括如下步骤：
[0150]
1)以热径向对流弥散理论研究为基础，依据热量守恒原理建立微热试验的理论模型，通过数学变换，建立理论模型不同渗流条件、不同参数条件下的标准曲线；
[0151]
2)通过微热试验，在上述半圆柱形砂槽模拟承压含水层系统中进行不同渗流条件和不同激发强度下的微热试验，通过传感器获取实测数据，绘制实测数据曲线；
[0152]
3)采用配线法将标准曲线与微热试验实测数据曲线进行匹配，记录对应的坐标值，通过计算得到含水层导热系数，通过相关公式推导得到岩土体导热系数、含水层热弥散度等其余热物性参数。
[0153]
本次室内试验研究共分为：不考虑流速情况下、流速为9.3
×
10-3
cm/s、6.82
×
10-3
cm/s、4.34
×
10-3
cm/s四种流速条件，每种流速条件下又进行三种不同温度激发强度下的微热试验。注入热水量根据导热管的半径以及含水层厚度计算而来，约800ml。以主孔探头数据作为计算参数的数据，每组试验进行两组平行试验，共计24组。
[0154]
根据微热试验计算含水层热物性参数的步骤和方法，首先利用grapher绘图软件绘制t
*d-τ关系的标准曲线，不考虑流速情况下的t
*d-τ关系曲线如图2所示，在考虑流速情况下，即t
*d-τ关系曲线如图3所示，然后根据试验数据在相同模的透明双对数纸上作实测曲线，使实测曲线坐标原点与标准曲线坐标原点保持同一高度，通过平移实测曲线时间坐标轴t来匹配实测曲线与标准曲线；任取一匹配点，记下匹配点的对应坐标[τ]值和[t]值，记录拟合标准曲线的[α]值；根据公式计算出含水层滞止导热系数与含水层有效导热系数，并可以反推出含水层热机械弥散系数与含水层热弥散度。其中不考虑流速情况下参数计算的配线图如图8至图10所示，滞止导热系数、含水层热容量与根据式(47)反推的岩土体导热系数计算结果见表1和表2。考虑流速情况下参数计算的配线图如图11至图13所示，含水层有效导热系数、含水层热机械弥散系数与根据式(48)反推的含水层热弥散度计算结果见表3和表4。
[0155]
表1不考虑流速情况下的微热试验模型计算含水层导热系数的结果
[0156][0157]
表2岩土体导热系数计算结果
[0158][0159]
表2中，水的导热系数和热容量根据经验值取得，含水层的热容量根据配线数据α求得，依据(ρc)
fs
＝θ(ρc)f+(1-θ)(ρc)s求得岩土体的热容量(ρc)s，最后依据，最后依据求出岩土体导热系数λs。
[0160]
从表1和表2可以看出，本次室内模拟试验的含水层孔隙度为θ＝0.33，(ρc)f＝4.18
×
106j/(m3·
℃)，计算求得岩土体导热系数的平均值为4.465w/(m
·
℃)。本次试验采
用的是粒径在0.25mm-0.50mm的中细砂。根据查找相关手册和文献，中细砂的导热系数一般在1.7～5.0w/(m
·
℃)范围内，本次试验求取的岩土体导热系数刚好在此范围内，由此也可证明微热试验确定含水层导热系数以及岩土体导热系数的准确性和可行性。
[0161]
表3考虑流速情况下的微热试验模型计算含水层导热系数的结果
[0162][0163]
表4含水层热弥散度计算结果
[0164][0165]
从表3和表4可以看出，根据不考虑流速计算得到的滞止导热系数，可以反推出热机械弥散系数与热弥散度。通过微热试验理论进行室内微热试验，操作简便，计算结果精确，试验周期短，能够较好的求出含水层的热物性参数。