一种斜拉桥模态跃迁试验测试装置及模态跃迁分析方法

1.本发明涉及桥梁动力分析及测试技术领域，具体涉及一种斜拉桥模态跃迁试验测试装置及模态跃迁分析方法。


背景技术：

2.现代斜拉桥的发展是桥梁工程师最引以为豪的成就之一。从某种意义来说，其结构参数失谐不可避免。这里所谓的“失谐”是引自周期或对称结构振动分析的专业术语，指结构损伤、材料性能老化、安装误差等引起的实际参数与设计参数的偏差，其对应于结构参数改变。例如大跨斜拉桥结构中，如拉索施工中的张拉误差、锚固损失、钢丝应力松弛及索力的测量误差等都会使实际索力偏离设计值，引起拉索拉力失谐。而运营过程中不可避免出现的材料老化、拉索锈蚀、疲劳损伤、以及节点开焊、梁体裂纹等现有桥梁存在的损伤与病害均可视为结构参数失谐。
3.振动模态跃迁发生时：失谐前后某两阶振型之间顺序相互交换、振型与频率之间不再满足原来的对应关系。密索体系的现代斜拉桥在步入千米级、悬索桥步入两千米主跨级时代后，风致振动和地震响应分析是常规计算内容，而这些动力响应分析的第一步就是确定结构频率、振型等基本动力特性，如这些基本动力特性确定有误，势必影响动力响应分析结果。现有技术中，已有动力损伤识别指标如：局部频率变化率指标和单元模态应变能变化率指标、动力损伤定位指标等，均是利用结构模态参数为依据来进行结构的损伤检测定位。结构模态跃迁后，振型与频率的之间不再是一一对应的关系，利用振型得到的动力损伤识别指标进行结构损伤检测时，也将会出现错误判断。同时，在土木工程领域尤其是大跨斜拉桥结构中对模态跃迁现象的研究有限，其对结构会造成怎样的影响和后果还未引起人们的充分认识和足够重视，针对该问题的试验装置也未有开发。


技术实现要素：

4.针对现有技术的上述不足，本发明提供了一种斜拉桥模态跃迁试验测试装置及模态跃迁分析方法，能够准确分析出斜拉桥模态跃迁的临界点的同时，能够通过试验测试装置观察到模态跃迁现象，方便研究模态跃迁现象。
5.为达到上述发明目的，本发明所采用的技术方案为：
6.提供一种斜拉桥模态跃迁试验测试装置，其包括底座，底座上竖直设置有桥塔，桥塔上设置有主梁，主梁上滑动设置有若干滑块，桥塔的顶端连接有若干拉索，拉索的上端与桥塔的顶端可拆卸连接，拉索的下端穿过滑块可拆卸连接有配重块；还包括用于测量主梁、桥塔和拉索动位移的激光位移计，激光位移计连接动态数据采集系统。
7.实际中拉索在装配在主梁与索塔之间的过程中，各根拉索依次装配，拉索的装配以及索力的调整对斜拉桥的整体刚度影响很大，使得装配和调索的难度较高，为了保证每个拉索的成桥索内力值与设计的参数值一致，需要不断的对拉索的拉力值进行调整。本发明提供的斜拉桥模态跃迁试验测试装置通过在拉索的活动端设置配重块将所有需要装配
的拉索的内力达到要求后，对拉索与主梁连接位置进行标记，再将所有拉索与主梁锁定，保证拉索的内力与设计值一致的同时省去了繁琐的调索过程。方便对斜拉桥模态跃迁现象的研究。
8.进一步的，滑块垂直于主梁设置，且滑块的两端均设置有供拉索穿过的开孔。
9.进一步的，滑块上设置有滑块锁定结构，滑块锁定结构包括螺纹孔和与螺纹孔啮合连接的螺栓，螺栓与主梁抵接。
10.进一步的，开孔处设置有拉索锁定结构，拉索锁定结构包括垂直于开孔设置的螺纹锁定孔，螺纹锁定孔啮合设置有锁定杆，锁定杆位于开孔内的一端转动连接有锁定块，锁定杆的另一端伸出螺纹锁定孔。
11.一种采用斜拉桥模态跃迁试验测试装置进行模态跃迁分析的方法，包括如下步骤：
12.s1；建立斜拉桥基准模型，采用若干个失谐参数均方差σ对斜拉桥基准模型进行失谐模拟，得到失谐参数均方差不同的斜拉桥失谐模型；
13.s2；对所有的斜拉桥失谐模型使用模态分析法，得到不同斜拉桥失谐模型的频率fi和振型向量φi；
14.s3；根据频率fi和振型向量φi计算得到斜拉桥结构发生模态跃迁时的失谐参数均方差σ'；
15.s4；提取失谐参数均方差σ'对应的斜拉桥失谐模型的工况参数k，使用工况参数k对斜拉桥模态跃迁试验测试装置进行调整；
16.s5；对采用工况参数k调整后的斜拉桥模态跃迁试验测试装置进行敲击，并使用动态数据采集系统对调整后的斜拉桥模态跃迁试验测试装置进行实时数据采集，使用polymax方法进行模态参数识别得到调整后的斜拉桥模态跃迁试验测试装置的频率fm和振型向量φm，观察斜拉桥模态跃迁试验测试装置的形态变化以及频率fm和振型向量φm的数值变化，实现对斜拉桥模态跃迁现象的研究。
17.进一步的，s1中采用的失谐参数均方差值的选取步骤如下：
18.a1；提出失谐参数均方差σi＝0，并提出失谐参数均方差步进值δσ；
19.a2；将失谐参数均方差σi使用改进后的randn函数生成包括n个随机数的随机数组；若随机数组中的最小值大于-1，则将失谐参数均方差σi作为单位元放入合集p，并进入步骤a3；否则，进入步骤a4；
20.a3；令σi＝σi+δσ，并返回步骤a2；
21.a4；选取合集p中单位元的最大值作为最大失谐参数均方差σ
max
，则σ∈[0，σ
max
]。
[0022]
进一步的，a2中改进后的randn函数为使用rng('default')命令将使用的随机数生成函数的设置重置为其默认值。
[0023]
改进后的randn函数使得不同的失谐参数均方差生成的随机数组具有相同的变化规律，具有可对比性，从而能够直观的体现失谐参数均方差与失谐程度之间的关系。
[0024]
进一步的，失谐参数均方差包括若干种失谐模式的均方差，失谐模式包括索力失谐、梁段刚度失谐和质量分布失谐中的一种或多种。
[0025]
进一步的，s3的具体步骤如下：
[0026]
s31；绘制出频率fi随失谐参数均方差σ变化的频率曲线图；
[0027]
s32；根据频率曲线图确定频率曲线发生转向时的阶数i'，频率曲线发生转向时即为斜拉桥发生模态跃迁；
[0028]
s33；计算出第i'阶频率曲线的曲率因子并绘制频率曲率因子变化图：
[0029][0030]
其中，curv
i'
为第i'阶频率曲率因子；ω
i'
为第i'阶频率曲线对σ的一阶导数；ω
′
i'
为第i'阶频率曲线对σ的二阶导数；
[0031]
s34；根据频率曲率因子变化图得到斜拉桥结构发生模态跃迁时的失谐参数均方差σ'；
[0032]
s35；使用模态置信度准则mac对失谐参数均方差σ'进行验证；模态置信度准则的表达式如下：
[0033][0034]
其中，φ
i'
为失谐参数均方差σ'的斜拉桥失谐模型的模型向量，φj为失谐参数均方差σ'
±
δσ的斜拉桥失谐模型的模型向量；t为数学转置运算符号；i'和j均为频率阶数；
[0035]
验证方法为：当i'＝j，mac
i'j
值接近0，并且i'≠j，mac
i'j
值接近1时，则σ'为斜拉桥结构发生模态跃迁时的失谐参数均方差；否则，重新提出失谐参数均方差步进值δσ'作为步骤a1中的δσ，返回步骤a2，并且使δσ'＜δσ。
[0036]
进一步的，步骤s34中，若频率曲率因子变化图的峰值不明显，则重新提出失谐参数均方差步进值δσ”作为步骤a1中的δσ返回步骤a2，并且使δσ”＜δσ。
[0037]
本发明的有益效果为：
[0038]
1、本斜拉桥模态跃迁试验测试装置通过设置滑块的数量和位置，能够模拟出实际斜拉桥的拉索数量以及拉索与主梁的连接位置；拉索对索塔和主梁的拉力由配重块模拟得到；当得到斜拉桥发生模态跃迁临界点时的工况后，复刻在试验测试装置上，能够直观的帮助我们观察斜拉桥的情况；方便调节工况，能够辅助进行更多的验证性试验。
[0039]
2、本发明提出的模态跃迁的分析方法通过引入失谐参数均方差对斜拉桥基准模型进行失谐模拟，无论是在研究斜拉桥索力失谐还是质量失谐时，都满足斜拉桥结构动力特性。模拟出的失谐的斜拉桥模型与实际失谐状态下的斜拉桥相近，从而使模态跃迁的分析结果贴近实际，能够为斜拉桥的模态跃迁的研究提供研究手段和研究环境，从而能够帮助完善斜拉桥的模态跃迁现象的研究。模态跃迁分析方法给出了失谐模拟方法、模态跃迁发生后从频率和振型两方面进行定量表征的合理指标。
附图说明
[0040]
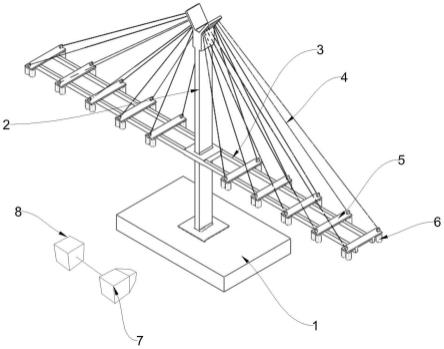
图1为斜拉桥模态跃迁试验测试装置的立体结构示意图；
[0041]
图2为滑块锁定结构剖视示意图；
[0042]
图3为拉索锁定结构剖视示意图；
[0043]
图4为四个失谐参数均方差生成的随机数组曲线图；
[0044]
图5为频率随失谐参数均方差变化的频率曲线图；
[0045]
图6为mac值与阶数关系的斜方图；
[0046]
图7为curv
16
值与失谐参数均方差的关系图。
[0047]
其中，1、底座；2、桥塔；3、主梁；4、拉索；5、滑块；6、配重块；7、激光位移计；8、动态数据采集系统；9、开孔；10、螺栓；11、锁定杆；12、锁定块。
具体实施方式
[0048]
下面对本发明的具体实施方式进行描述，以便于本技术领域的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。
[0049]
如图1所示，一种斜拉桥模态跃迁试验测试装置，其包括底座1，底座1上竖直设置有桥塔2，桥塔2上设置有主梁3，主梁3上滑动设置有若干滑块5，桥塔2的顶端连接有若干拉索4，拉索4的上端与桥塔2的顶端通过螺栓10可拆卸连接，拉索4的活动端穿过滑块5通过螺栓10可拆卸连接有配重块6；还包括用于测量主梁3、桥塔2和拉索4动位移的激光位移计7，激光位移计7对准实验测试装置整体，激光位移计7连接有动态数据采集系统8。滑块5垂直于主梁3设置，且滑块5的两端均设置有供拉索4穿过的开孔9。如图2所示，滑块5上设置有滑块锁定结构，滑块锁定结构包括螺纹孔和与螺纹孔啮合连接的螺栓10，螺栓10与主梁3抵接。如图3所示，开孔9处设置有拉索锁定结构，拉索锁定结构包括垂直于开孔9设置的螺纹锁定孔，螺纹锁定孔啮合设置有锁定杆11，锁定杆11位于开孔9内的一端转动连接有锁定块12，锁定杆11的另一端伸出螺纹锁定孔。本试验模型类似于有限元空间杆系模型的双主梁模型，制作时应满足刚度和质量相似，且刚度和质量的分配合理，与实际结构相符合。也可以采用单主梁式或者三主梁式进行模型制作。
[0050]
本发明中斜拉桥模态跃迁试验测试装置的工作原理及使用流程：
[0051]
根据实际的斜拉桥或者模拟出的斜拉桥的工况参数选择滑块5的数量，并在主梁3上滑动滑块5，使所有滑块5与工况参数中拉索4的连接位置相同，旋拧螺栓10，螺栓10与主梁3抵接锁定滑块5与主梁3之间的位置；将拉索4的上端与桥塔2的上端连接，拉索4的下端穿过开孔9，且拉索4的根据工况参数选择配重块6重量，将所有拉索4与相应的配重块6进行连接，接着旋拧锁定杆11，锁定块12随着锁定杆11的旋拧向锁定孔相对的开孔9侧壁移动，锁定块12与开孔9侧壁抵接，将位于锁定块12与开孔9侧壁之间的拉索4固定。取下拉索4下端的配重块6即可对斜拉桥进行敲击发生振动，通过激光位移计7对桥塔2、主梁3和拉索4的动位移进行实时测量，激光位移计7测量得到的动态数据传输至动态数据采集系统8中。
[0052]
本斜拉桥模态跃迁试验测试装置通过设置滑块的数量和位置，能够模拟出实际斜拉桥的拉索数量以及拉索与主梁的连接位置；拉索对索塔和主梁的拉力由配重块模拟得到；当得到斜拉桥发生模态跃迁临界点时的工况后，复刻在试验测试装置上，能够直观的帮助我们观察斜拉桥的情况；方便调节工况，能够辅助进行更多的验证性试验。
[0053]
本实施例中，一种采用斜拉桥模态跃迁试验测试装置进行模态跃迁分析的方法，包括如下步骤：
[0054]
s1；建立具有六对拉索的斜拉桥基准模型，使用选取后的四个失谐参数均方差对斜拉桥基准模型进行失谐模拟，得到四个失谐参数均方差不同的斜拉桥失谐模型；失谐参
数均方差包括若干种失谐模式的均方差，失谐模式包括索力失谐、梁段刚度失谐和质量分布失谐中的一种或多种。
[0055]
四个失谐参数均方差值的选取步骤如下：
[0056]
a1；提出失谐参数均方差σi＝0，并提出失谐参数均方差步进值δσ＝0.008；
[0057]
σi等于0时，代表斜拉桥基准模型未失谐的情况。
[0058]
a2；将失谐参数均方差σi使用改进后的randn函数生成包括24个随机数(即为失谐参数)的随机数组；若随机数组中的最小值大于-1，则将失谐参数均方差σi作为单位元放入合集p，并进入步骤a3；否则，进入步骤a4；
[0059]
改进后的randn函数为增加rng('default')命令的randn函数。在本发明的其他实施例中，随机数的数量可以为20、22、26、28或30等。24个随机数在满足能够模拟出斜拉桥的失谐状态下减少了计算数量。控制生成的随机数组的最小值大于-1，防止刚度或质量矩阵为负。
[0060]
a3；令σi＝σi+δσ，并返回步骤a2；
[0061]
a4；选取合集p中单位元的最大值作为最大失谐参数均方差σ
max
，则σ∈[0，σ
max
]。
[0062]
通过上述a1-a4步骤试验得出本实施例中σ
max
＝0.3200，在这里选取出的四个σ分别为0.0025、0.0750、0.1750和0.3200。失谐参数均方差的试验步骤一致，在此不对试验具体过程多做赘述。将上述四个失谐参数均方差分别带入改进后的randn函数生成四组随机数组，并绘制出如图4所示的四个随机数组的曲线图，由图4可知，随着失谐参数均方差的增加，曲线的变化程度即模拟出的失谐程度随之增大。改进后的randn函数使得不同的失谐参数均方差生成的随机数组具有相同的变化规律，具有可对比性，从而能够直观的体现失谐参数均方差与失谐程度之间的关系。
[0063]
s2；对所有的斜拉桥失谐模型使用模态分析法，得到不同斜拉桥失谐模型的频率fi和振型向量φi；
[0064]
s3；根据频率fi和振型向量φi计算得到斜拉桥结构发生模态跃迁时的失谐参数均方差σ'；
[0065]
s31；绘制出如图5所示的频率fi随失谐参数均方差σ变化的频率曲线图；
[0066]
s32；根据频率曲线图确定频率曲线发生转向时的阶数i'，频率曲线发生转向时即为斜拉桥发生模态跃迁；
[0067]
如图5所示，在本实施例中第16阶频率随失谐参数均方差的变化曲线与第17阶频率随失谐参数均方差的变化曲线在l1处发生了转向，即i'＝16。
[0068]
s33；计算出第i'阶频率曲线的曲率因子并绘制出如图7所示的频率曲率因子变化图：
[0069][0070]
其中，curv
i'
为第i'阶频率曲率因子；ω
i'
为第i'阶频率曲线对σ的一阶导数；ω
i'
通过将σ带入“gradient()”函数计算得到；ω
′
i'
为第i'阶频率曲线对σ的二阶导数；ω
′
i'
通过将σ带入“del2()”函数计算得到；
[0071]
s34；根据如图7所示的频率曲率因子变化图得到斜拉桥结构发生模态跃迁时的失
谐参数均方差σ'＝0.2450；
[0072]
若频率曲率因子变化图的峰值不明显，则重新提出失谐参数均方差步进值δσ”作为步骤a1中的δσ返回步骤a2，并且使δσ”＜δσ。提出变化阈值δk，当σ对应的频率曲率因子与σ
±
δσ所对应的频率曲率因子之间的差值大于变化阈值δk时，为峰值变化明显，否则，为峰值变化不明显。
[0073]
s35；使用模态置信度准则mac对失谐参数均方差σ'进行验证；模态置信度准则的表达式如下：
[0074][0075]
其中，φ
i'
为失谐参数均方差σ'＝0.2450的斜拉桥失谐模型的模型向量，φj为失谐参数均方差σ'
±
δσ的斜拉桥失谐模型的模型向量；t为数学转置运算符号；i'和j均为频率阶数；本实施例中φj为失谐参数均方差σ'+δσ＝0.2530的斜拉桥失谐模型的模型向量。
[0076]
验证方法为：当i'＝j，mac
i'j
值接近0，并且i'≠j，mac
i'j
值接近1时，则σ'为斜拉桥结构发生模态跃迁时的失谐参数均方差；否则，重新提出失谐参数均方差步进值δσ'作为步骤a1中的δσ，返回步骤a2，并且使δσ'＜δσ。
[0077]
计算mac
i'j
{i'＝16、17、18、19、20；j＝16、17、18、19、20}，并绘制出如图6所示的mac的斜方图，由图6中可知，mac
16-16
值和mac
17-17
值接近0，而mac
16-17
值和mac
17-16
值接近1，则σ'＝0.2450为本实施例中斜拉桥结构发生模态跃迁时的失谐参数均方差。
[0078]
s4；提取失谐参数均方差σ'＝0.2450对应的斜拉桥失谐模型的工况参数k，使用工况参数k对斜拉桥模态跃迁试验测试装置进行调整；
[0079]
对斜拉桥模态跃迁试验测试装置调整的包括：调整滑块5的位置和调整配重块6的重量。
[0080]
s5；对采用工况参数k调整后的斜拉桥模态跃迁试验测试装置进行敲击，并使用动态数据采集系统8对调整后的斜拉桥模态跃迁试验测试装置进行实时数据采集，使用polymax方法进行模态参数识别得到调整后的斜拉桥模态跃迁试验测试装置的频率fm和振型向量φm，观察斜拉桥模态跃迁试验测试装置的形态变化以及频率fm和振型向量φm的数值变化，实现对斜拉桥模态跃迁现象的研究。