基于波数域椭圆环滤波的复合材料分层损伤形貌检测方法

1.本发明涉及复合材料板分层损伤形貌检测方法，属于无损检测领域。


背景技术：

2.近年来复合材料相比传统金属材料受到了更多的关注。复合材料机体材料可以分为四种：聚合物基复合材料、金属基复合材料、陶瓷基复合材料和石墨基复合材料，其中聚合物基复合材料研究最早、规模最大。碳纤维增强聚合物(carbon fiber reinforced polymers,cfrp)作为一种典型的聚合物基复合材料，在航空航天、汽车、风力发电、机械制造等领域有着广泛的应用。
3.常见的碳纤维复合材料主要是纤维树脂层合板结构，组成复合材料的两种基材都保持原有的结构和性质，这就导致碳纤维复合材料相比于传统材料具有非均质性以及单向铺层的强各向异性。常见的多层碳纤维增强复合板是经过z向增强的多层碳纤维增强复合材料板。由于其特殊的力学性质，在碳纤维复合材料服役时，分层是常见的损伤形式。复合材料层合板在受到力的冲击时会发生偏转。冲击力导致纤维和树脂在受冲击的区域都被压碎，同时偏转的层合板触发层间剪切故障，导致分层。常见的冲击力有意外工具掉落、飞行器在空中与鸟类相撞等。除了冲击，材料受到拉伸、压缩、弯曲、疲劳、钻孔等也可能产生分层损伤，此外，复合板的疲劳和钻孔等加工也会造成分层，且分层是复合材料层合板在压力作用下的主要破坏模式。
4.分层损伤会造成结构整体的结构稳定性和强度急剧下降，甚至导致计划外的危险和巨大的损失。因此研究能够有效检测出复合材料结构内部分层的无损检测方法(non-destructive testing,ndt)，对于及时发现试件分层损伤并采取应对措施，延长试件使用寿命，减少社会经济损失，有着重要意义。复合材料检测过程中可以使用多种无损检测技术，如超声波检测、x射线检测、涡流检测、主动热成像等。其中，超声波检测灵敏度高、速度快、成本低、对人体无害，可定位并量化缺陷。因此，超声波检测可作为无损检测的一种手段进行分层检测。
5.对于板状结构，超声导波具有独特的优势。导波在板状传播距离远、衰减小，并且对板内部损伤敏感，适合作为复合材料板检测手段。但由于分层损伤属于材料内部损伤，在表面不可见，给损伤检测带来许多困难。而且分层损伤对材料结构的改变相对较小，因此损伤对信号的改变也更小，再加上复合材料的各向异性和频散特性，难以达到对复合材料的分层损伤准确检测。


技术实现要素：

6.本发明提出一种复合材料分层损伤形貌检测方法，将复合材料板的各向异性纳入考量，针对分层损伤引起的导波微小敏感模态进行提取和增强，实现较为准确的分层损伤的形貌检测。更为具体地，本发明首先根据各向异性材料本身的频散曲线，设计一个近似椭圆环的滤波器，然后通过激光多普勒测振仪测得w(x,y,t)全波场数据，经三维傅里叶变换
到频率-波数域，在波数域中进行椭圆环滤波，将分层损伤敏感模态增强，最后利用增强后的信号在空间域进行阈值成像，得到基本准确的分层损伤形貌图。本发明是通过以下技术方案实现的：
7.一种基于波数域椭圆环滤波的复合材料分层损伤形貌检测方法，包括以下步骤：
8.1)设计二维波数域椭圆环滤波器
9.a)由材料特性计算椭圆环滤波器所需参数
10.对于复合板，使复合材料基本力学特性计算出材料的相速度频散曲线，选定损伤成像所用的激励频率f，得到在此频率下的各个方向波数值，对于每一个方向的波数值进行正交分解，得到每个方向下的二维波数值：
11.k
θx
＝k
θ
·
cosθ
12.k
θy
＝k
θ
·
sinθ，
13.式中，θ表示导波传播方向与纤维0
°
的夹角，k
θx
表示k
θ
经过正交分解得到的x方向波数值，k
θy
表示k
θ
经过正交分解得到的y方向波数值；定义k0为θ＝0rad时x方向的波数值，定义为时y方向的波数值，即：
14.k0＝k
θx
，θ＝0rad
[0015][0016]
基于k0的值设定k
0min
和k
0max
的值；基于的值设定和的值；
[0017]
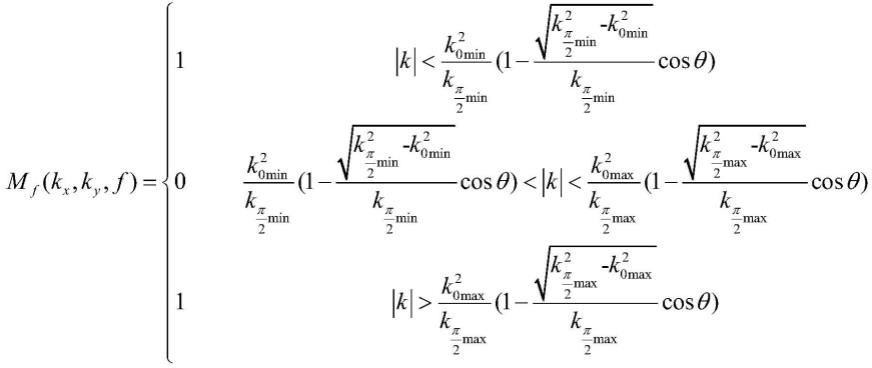
b)给出二维波数域椭圆环滤波器表达式mf(k
x
,ky,f)，其中k
x
和ky表示滤波器的两个波数域维度，mf(k
x
,ky,f)表达式所定义的滤波器是对二维波数域进行滤波，对于待处理的二维波数域数据，需要计算其波数模长，即
[0018][0019]
2)使用空气耦合超声换能器作为激励源，用激光多普勒测振仪扫描得到全波场数据w(x,y,f)，经三维傅里叶变换转换到频率-波数域中，得到数据w(k
x
,ky,f)；
[0020]
3)在数据w(k
x
,ky,f)中选出激励的中心频率，利用二维圆环波数滤波器，在波数域中进行椭圆环滤波，得到分层损伤敏感模态增强后的波场数据
[0021]
4)将分层损伤敏感模态增强后的波场数据进行逆傅里叶变换，回到空间
域，空间域波场数据为在空间域内进行能量成像，根据经验选取阈值th，得到分层损伤形貌检测图。
[0022]
进一步地，
[0023]
本发明的优点在于：
[0024]
1.本发明充分考虑了复合材料的各向异性，有利于形成准确的分层损伤图像。
[0025]
2.本发明在波数域中进行滤波，将时域信号难以分辨的模态分开了，并找出了其中对分层损伤较敏感的组分，通过椭圆滤波进行增强。
[0026]
3.本发明可以直接同时检测到损伤的位置和形貌，检测效率高，检测效果好。
[0027]
4.本发明对复合材料板的检测具有普适性，对各种类型的激励传感器都适用。指向性弱的压电传感器和指向性强的空气耦合传感器都可作为激励源。
附图说明
[0028]
图1是本发明的方法步骤示意图；
[0029]
图2是本发明计算得到的不同角度下波数的频散曲线图，图中曲线从下到上依次为0
°
、10
°
、20
°……
90
°
下波数的频散曲线；
[0030]
图3是本发明设计的二维波数域椭圆环滤波器示意图；
[0031]
图4是本发明的分层损伤成像结果图。
具体实施方式
[0032]
以下介绍的是作为本发明所述内容的具体实施方式，下面通过具体实施方式对本发明的所述内容作进一步的阐明。当然，描述下列具体实施方式只为示例本发明的不同方面的内容，而不应理解为限制本发明范围。
[0033]
本发明的复合材料分层损伤形貌检测方法，参见图1，该方法包括以下步骤：
[0034]
1)设计二维波数域椭圆滤波器
[0035]
a)根据材料特性参数设计滤波器参数
[0036]
本发明中采用的复合材料板试样为cfrp材料，由16层碳纤维[+45/-45/0/0]
2s
组成，试件总厚度为2mm，特性参数表如下表所示。
[0037][0038]
使用半解析有限元方法，计算由16个单层组成的复合板进行频散曲线。实验选取的激励频率用f表示，在此频率下a0模态为板中主要存在的模态，因此选择a0模态作为设计滤波器的参考模态。由于复合材料具有正交各向异性，所以各个方向的波数值不同，参见图2。对于每一个方向的波数值，按照下式对其进行正交分解，得到每个方向下的二维波数值。
[0039]kθx
＝k
θ
·
cosθ
[0040]kθy
＝k
θ
·
sinθ
[0041]
式中，θ表示导波传播方向与纤维0
°
的夹角，k
θx
表示k
θ
经过正交分解得到的x方向波数值，k
θy
表示k
θ
经过正交分解得到的y方向波数值。观察计算得到的二维波数值k
θx
和k
θy
，发现各个角度下的二维波数值组成的图形近似于一个椭圆，因此设计椭圆形滤波器。
[0042]
定义k0为θ＝0rad时x方向的波数值，定义为时y方向的波数值，
[0043][0044]
基于k0的值，结合信号带宽设定k
0min
和k
0max
的值，一般情况下可根据经验及实际情况适当调整。同理，基于的值，设定和的值，一般情况下可根据经验及实际情况适当调整。
[0045]
b)由上一步确定的滤波器参数，给出二维波数域椭圆环滤波器表达式mf(k
x
,ky,f)，其中k
x
和ky表示滤波器的两个波数域维度，f表示在选定的频率f下设计的二维波数域滤波器。滤波器示意图如图3所示。mf(k
x
,ky,f)表达式所定义的滤波器是对二维波数域进行滤波，因此对于待滤波的二维波数域数据，需要计算其波数模长，即
[0046][0047]
2)本发明中搭建了一个完全非接触式的超声检测系统，参见图2。使用空气耦合超声换能器作为激励源，用激光多普勒测振仪扫描得到全波场数据w(x,y,t)，将原始数据经三维傅里叶变换转换到频率-波数域中，得到数据w(k
x
,ky,f)。
[0048][0049]
3)在上述数据中选出激励的中心频率，在波数域中进行椭圆环滤波，得到分层损伤敏感模态增强后的波场数据由于分层损伤的存在，复合材料中正常传播的a0模态分别传播到分层上半部分和下半部分，两个子波既独立传播，又相互影响，产生了新的
模态，称之为分层损伤敏感模态。本发明在此步骤中，通过二维波数域滤波，对分层敏感模态进行了增强。
[0050][0051]
5)将分层损伤敏感模态增强后的数据进行逆傅里叶变换，回到空间域，波场数据为
[0052][0053]
在空间域内进行能量成像，根据经验选取阈值，作为最终的分层损伤形貌检测图，参见图4。本发明有效地对复合材料板分层损伤的形貌进行了检测。其中th为根据经验值选定的成像阈值。i(x,y)表示分层损伤形貌成像图中每个元素的灰度值。
[0054][0055]
尽管上文对本发明的具体实施方式进行了详细描述和说明，但是应该指明的是，本领域的技术人员可以依据本发明的精神对上述实施方式进行各种等效改变和修改，其所产生的功能作用在未超出说明书及附图所涵盖的精神时，均应在本发明的保护范围之内。