一种基于解析方法的多因素岩爆预测方法

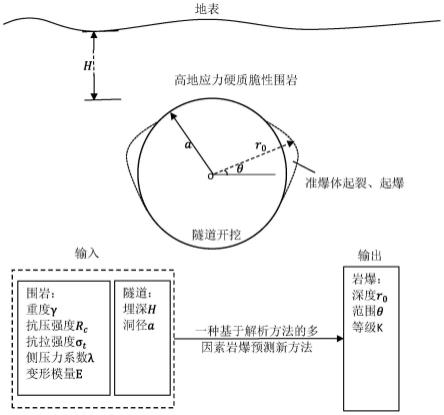
1.本发明涉及岩土工程技术领域，具体涉及一种基于解析方法的多因素岩爆预测方法。


背景技术：

2.隧道开挖后，围岩应力进行重分布。如果围岩应力处处小于岩体强度，则围岩仍然处于弹性状态；反之，当围岩某些区域的应力超过岩体强度，则围岩就会进入塑性或破坏状态。
3.岩爆是在坚硬完整或较完整的高地应力地区开挖隧道过程中发生的，其是岩石被挤压到弹性极限，岩体内积聚的能量突然释放所造成的岩石破坏现象，其实质是岩石脆性破坏。岩爆的突发性脆性破坏，造成岩片(块)脱离母体，猛然向临空方向抛弹射，经历快速“劈裂一剪折一弹射”的渐进破坏过程。
4.目前预测或评价岩爆等级的方法主要是应力强度比法，其采用单纯的应力强度比法，无法准确预测或者评价岩爆发生的位置和等级，例如：当侧压力大于1时，理论上拱顶环向应力最大，按照应力强度比理论，此时隧道拱顶应力强度比最大，拱顶更可能发生岩爆，且拱顶的岩爆等级相比于边墙更高。但在实际隧道工程中，在高地应力条件下，岩爆主要发生在隧道的边墙、拱腰等部位。比如，锦屏二级水电站引水隧洞，边墙、拱肩、拱顶、拱底的岩爆发生的次数分别为348、147、138、11次。实际岩爆发生现象和理论预测的发生位置明显不符。


技术实现要素：

5.本发明为了解决应力强度比法无法准确预测评价岩爆发生的位置和等级的问题，提供一种基于解析方法的多因素岩爆预测方法，其可考虑多种岩爆影响因素，对岩爆预测的位置和等级更加准确。
6.为解决现有技术问题，本发明采用技术方案为：一种基于解析方法的多因素岩爆预测方法，其特征在于，步骤为：
7.步骤1、推导非轴对称外荷载条件下隧道围岩脆性破坏的格里菲斯强度理论公式；
8.步骤2、推导非轴对称外荷载条件下圆形洞室的弹性理论解析解；
9.步骤3、推导岩爆孕育过程中的围岩起裂状态理论解析解；
10.步骤4、推导岩爆发展过程中的围岩起爆状态理论解析解；
11.步骤5、建立多因素岩爆预测模型。
12.进一步，步骤1的具体方法步骤为：
13.步骤1.1、根据格里菲斯强度理论的原理和内涵，分析脆性材料破裂的原因、破裂所需要的能量，以及破裂扩展的方向；
14.步骤1.2、根据格里菲斯强度理论主应力下的断裂判据，
15.格里菲斯强度判据为分段函数，在第一主应力σ1、第三主应力σ3的坐标系σ
1-σ3下
的格里菲斯强度判据，具体为：
16.当σ1+3σ3＜0时，σ3＜-σ
t
，
17.当σ1+3σ3＞0时，
18.步骤1.3、推导并提出非轴对称外荷载条件下，地下洞室围岩的格里菲斯起裂判据，
19.当(3σ
θ
+σr)(σ
θ
+3σr)＜4τ
rθ2
时，
20.判据为τ
rθ2
＜(σ
t
+σ
θ
)(σ
t
+σr)
ꢀꢀꢀ
(4a)
21.当(3σ
θ
+σr)(σ
θ
+3σr)＞4τ
rθ2
时，
22.判据为4τ
rθ2
＜8σ
t
(σ
θ
+σr)-(σ
θ-σr)2ꢀꢀꢀ
(4b)。
23.进一步，步骤2的具体方法步骤为：
24.步骤2.1、根据弹性力学相关理论，推导非轴对称外荷载条件下圆形洞室的弹性解；
25.非轴对称条件下弹性区应力场分量为：
[0026][0027][0028][0029]
其中，环向应力为σ
θ
，径向应力为σr，剪应力为τ
rθ
，洞径为a，围压为p，侧压力系数为λ；
[0030]
步骤2.2、根据格里菲斯起裂判据的选择条件及判据，推导非轴对称外荷载条件下圆形洞室的弹性应力分量组合表达式，根据应力场分量组合表达式可得应力场组合表达式为：
[0031][0032][0033][0034][0035]
进一步，步骤3的具体方法步骤为：
[0036]
步骤3.1、将应力场组合表达式带入起裂判据的选择条件(3σ
θ
+σr)(σ
θ
+3σr)＜4τ
rθ2
，得到起裂半径的隐函数，
[0037][0038]
令则上式简化为，
[0039]
[(1+λ)(2+r)+(1-λ)(1+3r2+2r)cos 2θ][(1+λ)(2-r)+(1-λ)(-1-3r2+6r)cos 2θ]
＜[(1-λ)(1+2r-3r2)sin 2θ]2ꢀꢀꢀ
(7b)
[0040]
当已知洞径a，侧压力系数λ时，求得围岩内任一位置(r,θ)处的判据选择条件；若不等式成立，则按照起裂判据
①
进行起裂评定；若不等式成立，则按照起裂判据
②
进行起裂评定；
[0041]
步骤3.2、将应力场组合表达式带入起裂判据公式(4a)和(4b)，
[0042]
将应力场组合表达式带入起裂判据公式(4a)得，
[0043][0044]
起裂判据
②
：将应力场组合表达式带入起裂判据公式(4b)得，
[0045][0046]
当已知围压p，侧压力系数λ，抗拉强度σ
t
，洞径a时，求得系数r，进而根据其与起裂半径r0的关系，求得具体位置θ处的起裂半径
[0047]
进一步，步骤4的具体方法步骤为：
[0048]
围岩起裂后，推导裂缝尖端应力或准爆体受力表达式；
[0049]
裂缝尖端应力等效为新洞室的洞壁应力，表达式为：
[0050]
σ
θ
(r,θ)＝p(1+λ)+2p(1-λ)cos 2θ
ꢀꢀꢀ
(9a)
[0051]
准爆体所受的平均压应力表达式为：
[0052][0053]
当压应力σc超过岩体抗压强度rc时，即σc＞rc时，围岩则发生起爆。
[0054]
进一步，步骤5的具体方法步骤为：
[0055]
步骤5.1、剖析应力强度比判据中岩爆等级、应力强度比k，环向应力σc，抗压强度rc之间的关系；
[0056]
步骤5.2、基于多因素环向应力σc表达式，建立多因素岩爆预测模型。
[0057]
与现有技术相比，本发明具有以下有益效果：
[0058]
本发明方法同时考虑多种岩爆影响因素，如隧道的洞径、埋深、侧压力系数，围岩的强度、变形特征参数等，可以更加准确的预测隧道岩爆发生在洞壁的具体位置，所在位置的准爆体范围和岩爆的等级。
[0059]
本发明在考虑各影响因素基础上，可从理论上证明，侧压力系数大于1的情况下，岩爆主要发生在边墙部位，且边墙部位的岩爆等级大于拱顶部位。从岩爆预测的准确性来说是满足工程要求的。
[0060]
本发明提供多因素岩爆预测新方法具有简便、快速、智能的特点。
附图说明
[0061]
图1为本发明一种基于解析方法的多因素岩爆预测方法的示意图；
[0062]
图2为本发明一种基于解析方法的多因素岩爆预测方法的技术流程图；
[0063]
图3为本发明一种基于解析方法的多因素岩爆预测方法的格里菲斯强度理论的起裂模式示意图；
[0064]
图4为本发明一种基于解析方法的多因素岩爆预测方法的格里菲斯强度判据的σ
1-σ3平面示意图。
具体实施方式
[0065]
下面结合附图对本发明的具体实施方式作进一步说明：
[0066]
本发明从隧道力学基本理论出发，基于符合岩石脆性破坏的格里菲斯脆性断裂强度理论，推导了洞室开挖——围岩应力重分布——围岩起裂——准爆体起爆的弹脆性解，提出了一种基于解析方法的多因素岩爆预测方法，可以更加准确预测岩爆的发生位置和等级。
[0067]
本发明提供一种基于解析方法的多因素岩爆预测方法，工艺流程如图2所示，具体按照以下步骤实施：
[0068]
步骤1、推导非轴对称外荷载条件下隧道围岩脆性破坏的格里菲斯强度理论公式，具体按照以下步骤实施：
[0069]
步骤1.1、深入剖析格里菲斯强度理论的原理、内涵；
[0070]
①
脆性材料内部存在着许多随机的微裂纹。在外力作用下，微裂纹的尖端附近产生很大的应力集中，当所聚集的能量达到一定值时，裂纹将开始扩展，如附图3所示。
[0071]
②
随着作用外力的增大，裂纹将沿着与最大拉应力成直角的方向扩展。在单轴压缩情况下，裂纹尖端处(pp
′
与裂纹交点)为最大拉应力。此时，裂纹将沿着与pp
′
垂直的方向扩展。最后，逐渐向最大主应力方向过度，即平行最大主应力的方向扩展。这一分析结果，很形象的揭示了在单轴压缩应力作用时劈裂破坏才是岩石破坏的最本质现象。
[0072]
③
当作用在裂纹尖端处的有效应力达到形成新裂纹所需要的能量时，裂纹开始扩展，如图4所示，其表达是为，其中，σ
t
裂纹尖端最大的拉应力，ρ裂纹的比表面能，c裂纹长半轴长度，e为弹性模量。
[0073]
以上基本思想明确的揭示了脆性材料破裂的原因、破裂所需要的能量，以及破裂扩展的方向。
[0074]
步骤1.2、深入剖析格里菲斯强度理论主应力下的断裂判据；
[0075]
应用弹性力学中的椭圆孔，可推导出格里菲斯强度判据。格里菲斯强度判据为分段函数，在第一主应力σ1、第三主应力σ3的坐标系σ
1-σ3下的格里菲斯强度判据，如图4所示，可具体描述为：
[0076]
①
当σ1+3σ3＜0时，σ3＜-σ
t
，在图中为一直线。表明当作用应力满足σ1+3σ3＜0时，不管σ1为何值时，只要满足σ3＝-σ
t
，岩石裂纹就开始扩展。
[0077]
②
当σ1+3σ3＞0时，在图中为二次曲线，且在点(3σ
t
，-σ
t
)与
①
中的直线段相接。当微裂纹随机分布与岩石中，其最有利于破裂的裂纹方向角为且
[0078]
步骤1.3、推导并提出非轴对称外荷载条件下地下洞室围岩的格里菲斯起裂判据。
[0079]
①
根据轴对称条件下圆形隧道的受力特征，可以认为：环向应力σ
θ
＝σ1，径向应力σr＝σ3，则满足圆形洞室的格里菲斯条件可表示为，
[0080]
(σ
θ-σr)2＝8σ
t
(σ
θ
+σr)
ꢀꢀꢀ
(1)
[0081]
②
根据非轴对称条件下圆形隧道的受力特征，环向应力σ
θ
≠σ1，径向应力σr≠σ3，因为此时存在剪应力τ
rθ
的作用。根据应力圆特征，
[0082][0083][0084]
此时，
[0085]
判别条件，σ1+3σ3＝0，等价于
[0086]
(3σ
θ
+σr)(σ
θ
+3σr)＝4τ
rθ2
ꢀꢀꢀ
(3a)
[0087]
对于判据
①
，σ3＝-σ
t
，等价于
[0088]
τ
rθ2
＝(σ
t
+σ
θ
)(σ
t
+σr)
ꢀꢀꢀ
(3b)
[0089]
对于判据
②
，等价于
[0090]
4τ
rθ2
＝8σ
t
(σ
θ
+σr)-(σ
θ-σr)2ꢀꢀꢀ
(3c)
[0091]
且当τ
rθ
＝0时，上式可退化到轴对称下的判别条件。
[0092]
综上，可得非轴对称荷载下隧道的起裂判据：
[0093]
①
当(3σ
θ
+σr)(σ
θ
+3σr)＜4τ
rθ2
时，
[0094]
τ
rθ2
＜(σ
t
+σ
θ
)(σ
t
+σr)
ꢀꢀꢀ
(4a)
[0095]
②
当(3σ
θ
+σr)(σ
θ
+3σr)＞4τ
rθ2
时，
[0096]
4τ
rθ2
＜8σ
t
(σ
θ
+σr)-(σ
θ-σr)2ꢀꢀꢀ
(4b)
[0097]
步骤2、推导非轴对称外荷载条件下圆形洞室的弹性理论解析解，具体按照以下步骤实施：
[0098]
步骤2.1、根据弹性力学相关理论，推导非轴对称外荷载条件下圆形洞室的弹性解；
[0099]
非轴对称条件下弹性区应力场分量为：
[0100][0101][0102][0103]
其中，环向应力为σ
θ
，径向应力为σr，剪应力为τ
rθ
，洞径为a，围压为p，侧压力系数为λ。
[0104]
步骤2.2、根据格里菲斯起裂判据的选择条件及判据，推导非轴对称外荷载条件下
圆形洞室的弹性应力分量组合表达式。
[0105]
根据应力场分量可得应力场组合表达式为：
[0106][0107][0108][0109][0110]
步骤3、推导岩爆孕育过程中的围岩起裂状态理论解析解，具体按照以下步骤实施：
[0111]
步骤3.1、将应力场组合表达式带入起裂判据的选择条件；
[0112]
将应力场组合表达式带入起裂判据的选择条件(3σ
θ
+σr)(σ
θ
+3σr)＜4τ
rθ2
得到关于起裂半径的隐函数，
[0113][0114]
令则上式可化简为，
[0115]
[(1+λ)(2+r)+(1-λ)(1+3r2+2r)cos 2θ][(1+λ)(2-r)+(1-λ)(-1-3r2+6r)cos 2θ]＜[(1-λ)(1+2r-3r2)sin 2θ]2ꢀꢀꢀ
(7b)
[0116]
上式是关于r、θ的隐式函数，当已知洞径a，侧压力系数λ时，就可以求得围岩内任一位置(r,θ)处的判据选择条件。若上述不等式成立，则按照起裂判据
①
进行起裂评定；若上述不等式成立，则按照起裂判据
②
进行起裂评定。
[0117]
步骤3.2、将应力场组合表达式带入起裂判据
①
、
②
。
[0118]
起裂判据
①
：将应力场组合表达式带入起裂判据
①
得，
[0119][0120][0121]
起裂判据
②
：将应力场组合表达式带入起裂判据
②
得，
[0122][0123]
上式是关于r、θ、r的隐式函数，当已知围压p，侧压力系数λ，抗拉强度σ
t
，洞径a时，就可以求得系数r，进而根据其与起裂半径r0的关系，进一步求得起裂半径也就是说，通过上式可以求得具体位置θ处的起裂半径r0。
[0124]
步骤4、推导岩爆发展过程中的围岩起爆状态理论解析解，具体按照以下步骤实施：
[0125]
步骤4.1、围岩起裂后，推导裂缝尖端应力或准爆体受力表达式；
[0126]
围岩起裂后，裂缝尖端应力可等效为新洞室的洞壁应力为，即
[0127]
σ
θ
(r,θ)＝p(1+λ)+2p(1-λ)cos 2θ
ꢀꢀꢀ
(9a)
[0128]
步骤4.2、推导准爆体所受的平均压应力表达式。
[0129]
准爆体所受的平均压应力为：
[0130][0131]
当压应力σc超过岩体抗压强度rc时，即σc＞rc时，围岩则发生起爆。
[0132]
步骤5、建立多因素岩爆预测模型，具体按照以下步骤实施：
[0133]
步骤5.1、剖析应力强度比判据中岩爆等级、应力强度比k，环向应力σc，抗压强度rc之间的关系；
[0134]
根据常用的应力强度比判据，岩爆等级、应力强度比k，环向应力σc，抗压强度rc之间的关系为，k＝σc/rc，且有：
[0135]
①
k《0.3，无岩爆；
[0136]
②
0.3≤k《0.5，弱岩爆；
[0137]
③
0.5≤k《0.7，中等岩爆；
[0138]
④
0.7≤k《0.9，强烈岩爆；
[0139]
⑤
0.9≤k，极强岩爆。
[0140]
步骤5.2、基于多因素环向应力σc表达式，建立多因素岩爆预测模型。
[0141]
根据围岩起爆状态理论解析中的准爆体所受的平均压应力公式，可计算出环向应力σc。当已知围岩的抗压强度rc时，根据应力强度比k与岩爆等级之间的关系，即可进行岩爆等级判断。
[0142]
本发明步骤1可准确推导出描述围岩脆性破坏的格里菲斯强度理论。
[0143]
采用格里菲斯强度理论，原理是：岩爆是在坚硬完整或较完整的高地应力地区开挖隧道过程中发生的，其是岩石被挤压到弹性极限，岩体内积聚的能量突然释放所造成的岩石破坏现象，其实质是岩石脆性破坏。岩爆是高地应力的产物，其是具有大量弹性应变能储备的硬质脆性岩体，由于洞室开挖，径向约束卸除，环向应力骤然增加，能量进一步集中，在集中应力作用下，产生突发性脆性破坏，造成岩片(块)脱离母体，猛然向临空方向抛弹射，经历快速“劈裂一剪折一弹射”的渐进破坏过程。一般的强度理论均将材料看作完整而连续的均匀介质。事实上，任何材料内部都存在着许多微细(潜在的)裂纹或裂隙，在力的作用下这此裂隙周围(尤其是在裂隙端部)将产生较大的应力集中。在这种情况下材料的破坏将不受自身强度控制，而是取决于其内部裂隙周围的应力状态。材料的破坏往往从裂隙端部开始，并且通过裂隙扩展而导致完全破坏。而岩石就是这种包含大量微裂纹和孔洞的脆性材料。因此格里菲斯理论为岩石破坏判据提供了一个重要理论基础。
[0144]
采用格里菲斯强度理论，优点在于：格里菲斯强度理论很好的揭示了脆性材料破裂的原因、破裂所需要的能量，以及破裂扩展的方向。格里菲斯强度理论能很好的描述岩爆中的岩石脆性破坏特征。
[0145]
本发明步骤2可准确推导出非轴对称外荷载条件下圆形洞室的弹性理论解析解。
[0146]
采用非轴对称外荷载条件下圆形洞室的弹性解析解，原理是：隧道开挖后，围岩应
力重分布，如果围岩应力处处小于岩体强度，则围岩仍然处于弹性状态；反之，当围岩某些区域的应力超过岩体强度，则围岩进入塑性或破坏状态。若围岩的局部区域的拉应力达到了极限抗拉强度，则产生局部受拉脆性破坏。岩爆是高地应力的产物，其是具有大量弹性应变能储备的硬质脆性岩体，由于洞室开挖，径向约束卸除，环向应力骤然增加，能量进一步集中，在集中应力作用下，产生突发性脆性破坏。
[0147]
采用非轴对称外荷载条件下圆形洞室的弹性解析解，其优点在于：岩爆是发生在高地应力条件下，在坚硬完整或较完整的岩体中，进行隧道开挖卸荷后发生的。非轴对称外荷载条件下圆形洞室的弹性解，是基本的弹性力学方程，推导得出可考虑各影响因素(如：洞径a，围压p，侧压力系数λ等)影响下的洞室弹性理论解。
[0148]
在本发明步骤3可准确推导出岩爆孕育过程中的围岩起裂状态理论解析。
[0149]
采用围岩起裂状态理论解析，原理是：岩爆的实质是岩石脆性破坏。岩爆是高地应力的产物。由于洞室开挖卸荷，在环向集中应力作用下，产生突发性脆性破坏，造成岩片(块)脱离母体，猛然向临空方向抛弹射，经历快速“劈裂一剪折一弹射”的渐进破坏过程。也就是说岩爆发生多是先起裂后爆出的。
[0150]
采用围岩起裂状态理论解析，其优点在于：在已知隧道基本参数(围压p，侧压力系数λ，抗拉强度σ
t
，洞径a)下，就能准确地求得围岩内任一位置(r,θ)处的起裂判据选择条件，进而进行起裂判据选择。根据起裂判据
①
或
②
，进行起裂半径r0或范围θ的计算。
[0151]
本发明步骤4可准确推导出岩爆发展过程中的围岩起爆状态理论解析。
[0152]
采用围岩起爆状态理论解析，其原理是：在脆性材料内部存在着许多随机的微裂纹。在外力作用下，微裂纹的尖端附近产生很大的应力集中，当所聚集的能量达到一定值时，裂纹将开始扩展。随着作用外力的增大，裂纹将沿着与最大拉应力成直角的方向扩展。在单轴压缩情况下，裂纹将沿着与pp
′
垂直的方向扩展。最后，逐渐向最大主应力方向过度，即平行最大主应力的方向扩展。格里菲斯强度很形象的揭示了在单轴压缩应力作用时劈裂破坏才是岩石破坏的最本质现象。
[0153]
采用围岩起爆状态理论解析，其优点在于：围岩岩爆遵循先起裂后起爆的孕育发展机制。在围岩内部发生围岩起裂以后，产生准爆体，准爆体受力进行调整，当准爆体的平均压应力σc超过岩体抗压强度rc时，则准爆体发生起爆，即产生岩爆灾害。
[0154]
本发明步骤5可准确建立多因素岩爆预测模型。
[0155]
采用岩爆多因素预测模型，其原理是：结合非轴对称外荷载下圆形洞室的弹性解和围岩格里菲斯起裂判据，就能得到围岩的弹脆性解答，进而能得到弹脆性条件下围岩的环向应力及准爆体所受的平均压应力。基于常用的应力强度比判据，根据应力强度比k就能判断岩爆的等级。
[0156]
采用岩爆多因素预测模型，其优点在于：对于实际隧道工程，可以方便得到围岩的侧压力系数λ、抗压强度rc、抗拉强度σ
t
、容重γ、弹性模量e、洞室的洞径a、位置角度θ，埋深h等参数。围压p与埋深h和容重γ的关系为p＝γh。而变形模量和抗压强度、抗拉强度有经验关系，也就是说只要知道岩体的变形模量，即可求得抗压强度rc和抗拉强度σ
t
。在已知隧道基本参数前提下，就能准确地求得围岩内任一位置(r,θ)处的起裂判据选择条件，进而根据起裂判据
①
或
②
，得到起裂半径r0和范围θ。当准爆体的平均压应力σc超过岩体抗压强度rc时，则发生起爆。同时根据应力强度比判据，判断岩爆发生的等级。
[0157]
实施例：
[0158]
一种基于解析方法的多因素岩爆预测方法，实施岩爆预测的详细过程如下：
[0159]
①
获取围岩和隧道的基本特征参数，包括隧道的洞径a、埋深h、侧压力系数λ，围岩的抗压强度rc、抗拉强度σ
t
，容重γ等。
[0160]
②
获取洞室弹性应力分量解及应力组合结果，如式(5a～6d)。
[0161]
③
将应力组合结果带入隧道围岩的格里菲斯起裂判据选择条件及判据表达式，如式(4a～4b)，判断围岩是否会发生起裂。
[0162]
⑤
若围岩发生起裂，根据起裂判据可获得起裂半径和起裂范围，如式(7a～8b)。
[0163]
⑥
根据起裂半径，计算准爆体的平均压应力，如式(9a～9b)。
[0164]
⑦
根据准爆体的强度应力比对岩爆等级进行预判。
[0165]
《引汉济渭工程超长深埋隧道岩爆防治技术研究》：
[0166]
引汉济渭工程秦岭隧洞某段，埋深660m，容重28.6kn/m3，围压19mp，变形模量38gpa，抗压强度80mpa，抗拉强度3.1mpa，侧压力系数1.25，洞径3.4m，实际为强岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为3.69m，进而可计算准爆体的平均压应力为114.4mpa。通过多因素岩爆预测模型判断，该段洞室为边墙强岩爆，与实际情况吻合较好。
[0167]
《引汉济渭工程超长深埋隧道岩爆防治技术研究》：
[0168]
引汉济渭工程秦岭隧洞某段，埋深800m，容重27kn/m3，围压22mp，变形模量35gpa，抗压强度130mpa，抗拉强度2.7mpa，侧压力系数1.19，洞径3.4m，实际为中岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为3.99m，进而可计算准爆体的平均压应力为66.71mpa。通过多因素岩爆预测模型判断，该段洞室为边墙中岩爆，与实际情况吻合较好。
[0169]
《引汉济渭工程超长深埋隧道岩爆防治技术研究》：
[0170]
引汉济渭工程秦岭隧洞某段，埋深1070m，容重28kn/m3，围压30mp，变形模量33gpa，抗压强度80mpa，抗拉强度2.7mpa，侧压力系数1.13，洞径3.4m，实际为强岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为4.34m，进而可计算准爆体的平均压应力为59.81mpa。通过多因素岩爆预测模型判断，该段洞室为边墙强岩爆，与实际情况吻合较好。
[0171]
《引汉济渭工程秦岭隧洞岩爆数值模拟与岩爆预测研究》：
[0172]
引汉济渭工程秦岭隧洞某段，埋深800m，容重27kn/m3，围压22mp，变形模量35gpa，抗压强度46mpa，抗拉强度2.5mpa，侧压力系数1.15，洞径3.4m，实际为强岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为4.07m，进而可计算准爆体的平均压应力为59.5mpa。通过多因素岩爆预测模型判断，该段洞室为边墙强岩爆，与实际情况吻合较好。
[0173]
《引汉济渭工程秦岭隧洞岩爆数值模拟与岩爆预测研究》：
[0174]
引汉济渭工程秦岭隧洞某段，埋深1070m，容重28kn/m3，围压29mp，变形模量33gpa，抗压强度105mpa，抗拉强度3.5mpa，侧压力系数1.05，洞径3.4m，实际为中岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为4.09m，进而可计算准爆体的平均压应力为54.1mpa。通过多因素岩爆预测模型判断，该段洞室为边墙中岩爆，与实际情况吻合较好。
[0175]
《拉林铁路桑珠岭隧道地应力场分析及岩爆预测研究》：
[0176]
拉林铁路桑珠岭隧道某段，埋深138m，容重24kn/m3，围压3.3mp，变形模量20gpa，抗压强度40mpa，抗拉强度1.1mpa，侧压力系数3.32，洞径3.8m，实际为无岩爆。根据以上参数及相关公式，可得洞室弹性应力分量。将应力组合结果带入隧道围岩起裂判据选择条件及判据表达式，边墙结果满足起裂判据
②
，则边墙围岩会发生起裂。根据起裂判据
②
，可获得围岩起裂半径为3.94m，进而可计算准爆体的平均压应力为7.5mpa。通过多因素岩爆预测模型判断，该段洞室为边墙无岩爆，与实际情况吻合较好。
[0177]
实施例1～6表明：通过该方法进行岩爆判断，结果准确，满足工程需求。一种基于解析方法的多因素岩爆预测方法可为其它隧道工程进行岩爆预测服务。