一种双相介质中横波、快纵波和慢纵波的解耦方法

1.本发明涉及勘探地球物理技术领域，尤其涉及一种双相介质中横波、快纵波和慢纵波的解耦方法。


背景技术：

2.双相介质理论是一种经典的研究地震波传播的理论方法。实际的地下介质富含大量含流体的孔隙，这些孔隙中的流体和固体骨架间存在相互作用，对地震波的传播有很大的影响。相比传统的单相介质理论，双相介质理论兼顾了地下介质中固体骨架和孔隙流体的性质，同时考虑了二者之间相互作用的影响，因而能够更加精确地描述地震波在地下的实际传播情况。不同特征波场的解耦是一种常用的地震波现象分析方法，有助于研究不同类型的波场传播机制，并在成像和反演中减少串扰影响，提高成像和反演的精度，但地震波在双相介质中传播时会产生快纵波、慢纵波和横波三种波类型，尤其是快纵波和慢纵波的耦合情况较复杂，不同于常规快慢波的耦合，目前基本没有方法能将它们完全分离。
3.在传统的单相介质波场解耦中，一种常用的方法是根据纵波和横波不同的偏振方向，利用内积运算将它们进行分离，这种方法首先使用特征分析求出纵波和横波的特征向量，得到二者相互正交的偏振方向，然后将整个波场分别通过内积映射到各自的偏振方向上来分离二者。但对于双相介质的情况，其中的快纵波和慢纵波的偏振方向并不是相互正交的，使用内积法将波场映射到某个波型的偏振方向上时，不能完全去除另一种波，因此传统单相介质波场解耦的方法不适用于双相介质的情况，无法完全分离双相介质中的三种波型，尤其是快纵波和慢纵波。
4.因此，亟需寻找一种双相介质中精确的波场解耦方法将快纵波、慢纵波和横波三种波型进行完全分离，从而能够更好地对各种波形的传播机制进行系统研究。


技术实现要素：

5.为解决上述技术问题，本发明公开了一种双相介质中横波、快纵波和慢纵波的解耦方法，基于biot双相介质理论，本发明使用亥姆霍兹分解对无耗散的biot方程求取散度和旋度，从而先将纵波和横波分离并得到二者的势波场；然后将特征分析法应用到纵波的势方程中，得到快纵波和慢纵波的偏振向量，根据二者不同的偏振方向，利用一次外积将快纵波和慢纵波从纵波势波场中分离，然后再作用一次外积来恢复它们的振幅和相位；最终得到分离的横波、快纵波和慢纵波波场。
6.为实现上述目的，本发明采用下述技术方案：
7.根据本发明实施例的一个方面，提出了一种双相介质中横波、快纵波和慢纵波的解耦方法。
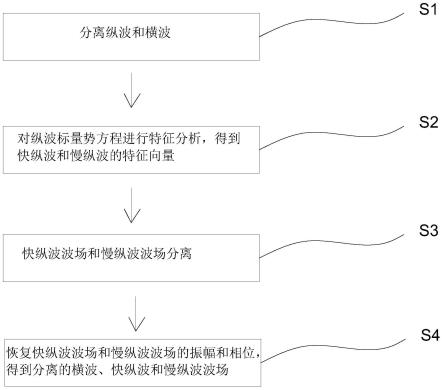
8.在一个实施例中，双相介质中横波、快纵波和慢纵波的解耦方法，包括以下步骤：
9.s1：对无耗散的biot方程利用亥姆霍兹分解求散度和旋度，得到纵波势方程和横波势方程，分离纵波和横波；
10.s2：对纵波势方程进行特征分析，得到快纵波和慢纵波的特征向量；
11.s3：将快纵波和慢纵波的特征向量分别与纵波标量势做外积，得到分离后的快纵波波场和慢纵波波场；
12.s4：恢复快纵波波场和慢纵波波场的振幅和相位。
13.可选地，步骤s1中，所述biot方程为：
[0014][0015][0016]
其中，us＝(u
solid_x
,u
solid_z
)
t
，uf＝(u
fluid_x
,u
fluid_z
)
t
，u
solid_x
和u
solid_z
为固相x和z方向位移分量，u
fluid_x
和u
fluid_z
为液相x和z方向位移分量，a、n、q、r为弹性参数，ρ
11
、ρ
12
、ρ
22
为质量系数，t为时间，x和z分别为水平和垂直方向；
[0017]
所述纵波势方程为：
[0018][0019][0020]
所述横波势方程为：
[0021][0022][0023]
其中，和分别为固相和液相的纵波标量势，和分别为固相和液相的横波矢量势。
[0024]
可选地，步骤s2中，对纵波势方程进行特征分析，得到快纵波和慢纵波的特征向量包括以下步骤：
[0025]
s21将纵波势方程转换为以下表达式：
[0026][0027][0028]
s22将步骤s21中得到的表达式转换到频率-波数域，得到以下表达式：
[0029][0030]
其中，和分别为θ
solid
和θ
fluid
的傅里叶变换，k
x
和kz分别为x和z方向的波数，ω为角频率；
[0031]
s23记步骤s22中表达式系数矩阵为则m的特征值λ为
[0032][0033]
其中，参数c和d分别表示为：
[0034][0035][0036]
m的特征向量为
[0037][0038][0039]
其中，和分别是a
fast
和a
slow
的傅里叶变换，a
fast
和a
slow
是快纵波和慢纵波的特征向量。
[0040]
可选地，步骤s3中，将特征向量a
fast
与纵波标量势向量θ做外积，得到分离后的慢纵波波场u
slow
＝a
fast
×
θ；将特征向量a
slow
与纵波标量势向量θ做外积，得到分离后的快纵波波场u
fast
＝a
slow
×
θ，其中，a
fast
和a
slow
由和经反傅里叶变换得到，标量势向量θ由固相和液相标量势组成，表示为：θ＝[θ
solid
,θ
fluid
]
t
。
[0041]
可选地，步骤s4包括：
[0042]
s41通过特征向量a
fast
和a
slow
分别构建两个矩阵a
slow
＝[a
fast a
slow
]和a
fast
＝[a
slow a
fast
]，并通过以下步骤求取两个辅助向量b
fast
和b
slow
：
[0043]
设a
fast
＝(x1,y1)，a
slow
＝(x2,y2)，x和y分别为向量的横纵坐标，计算x1y
2-x2y1的值。若x1y
2-x2y1的值小于0，则b
fast
＝(-y1,x1)，b
slow
＝(y2,-x1)；若x1y
2-x2y1的值大于0，则b
fast
＝(y1,-x1)，b
slow
＝(-y2,x1)；
[0044]
s42利用u
fast
、u
slow
、a
fast
、a
slow
、b
fast
、b
slow
得到恢复振幅和相位的快纵波波场和慢纵波波场其中θ
fast
＝[θ
solid_fast
θ
fluid_fast
]
t
，θ
slow
＝[θ
solid_slow
θ
fluid_slow
]
t
，θ
solid_fast
为固相快纵波，θ
fluid_fast
为液相快纵波，θ
solid_slow
为固相慢纵波，θ
fluid_slow
为液相慢纵波。
[0045]
本发明的有益效果是，本发明的解耦方法为先分离纵波和横波，再在分离得到的纵波中将快纵波和慢纵波分离。本发明首先利用亥姆霍兹分解法将初始波场分解为纵波和横波，并得到二者的势方程；然后利用特征分析，在纵波势方程中求出快纵波和慢纵波的特征值和特征向量，得到二者的偏振方向；根据二者不同的偏振方向，作用第一次外积将二者分离，并在此之上再作用一次外积，从而得到真振幅的快纵波和慢纵波波场。该方法不仅能够有效地将快纵波、慢纵波和横波进行完全分离，而且还恢复了快纵波和慢纵波的振幅和
相位，从而可以大大提高后续成像和反演等工作的质量。
附图说明
[0046]
图1为本发明一实施例示出的一种双相介质中横波、快纵波和慢纵波的解耦方法流程图；
[0047]
图2为地震波在双层的双相介质中传播的波场快照，其中，(a)为固相x方向速度分量，(b)为固相z方向速度分量，(c)为液相x方向速度分量，(d)为液相z方向速度分量；
[0048]
图3为利用本发明的方法分离得到的纵波势波场和横波势波场的快照，其中，(a)为固相纵波势波场，(b)为液相纵波势波场，(c)为固相横波势波场，(d)为液相横波势波场；
[0049]
图4为利用本发明的方法分离得到的快纵波和慢纵波波场快照，其中，(a)为固相快纵波，(b)为固相慢纵波，(c)为液相快纵波，(d)为液相慢纵波；
[0050]
图5为利用本发明的方法的分离误差，其中，(a)为固相误差，(b)为液相误差。
具体实施方式
[0051]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0052]
一种双相介质中横波、快纵波和慢纵波的解耦方法，如图1所示，包括以下步骤：
[0053]
s1：对无耗散的biot方程利用亥姆霍兹分解求散度和旋度，得到纵波势方程和横波势方程，分离纵波和横波；
[0054]
s2：对纵波势方程进行特征分析，得到快纵波和慢纵波的特征向量；
[0055]
s3：将快纵波和慢纵波的特征向量分别与纵波标量势做外积，得到分离后的快纵波波场和慢纵波波场；
[0056]
s4：恢复快纵波波场和慢纵波波场的振幅和相位。
[0057]
可选地，步骤s1中，所述biot方程为：
[0058][0059][0060]
其中，us＝(u
solid_x
,u
solid_z
)
t
，uf＝(u
fluid_x
,u
fluid_z
)
t
，u
solid_x
和u
solid_z
为固相x和z方向位移分量，u
fluid_x
和u
fluid_z
为液相x和z方向位移分量，a、n、q、r为弹性参数，ρ
11
、ρ
12
、ρ
22
为质量系数，t为时间，x和z分别为水平和垂直方向；
[0061]
所述纵波势方程为：
[0062][0063][0064]
所述横波势方程为：
[0065][0066][0067]
其中，和分别为固相和液相的纵波标量势，和分别为固相和液相的横波矢量势。
[0068]
可选地，步骤s2中，对纵波势方程进行特征分析，得到快纵波和慢纵波的特征向量包括以下步骤：
[0069]
s21将纵波势方程转换为以下表达式：
[0070][0071][0072]
s22将步骤s21中得到的表达式转换到频率-波数域，得到以下表达式：
[0073][0074]
其中，和分别为θ
solid
和θ
fluid
的傅里叶变换，k
x
和kz分别为x和z方向的波数，ω为角频率；
[0075]
s23记步骤s22中表达式系数矩阵为则m的特征值λ为
[0076][0077]
其中，参数c和d分别表示为：
[0078][0079][0080]
m的特征向量为
[0081][0082][0083]
其中，和分别是a
fast
和a
slow
的傅里叶变换，a
fast
和a
slow
是快纵波和慢纵波的特征向量。
[0084]
可选地，步骤s3中，将特征向量a
fast
与纵波标量势向量θ做外积，得到分离后的慢纵波波场u
slow
＝a
fast
×
θ；将特征向量a
slow
与纵波标量势向量θ做外积，得到分离后的快纵波
波场u
fast
＝a
slow
×
θ，其中，a
fast
和a
slow
由和经反傅里叶变换得到，标量势向量θ由固相和液相标量势组成，表示为：θ＝[θ
solid
,θ
fluid
]
t
。
[0085]
可选地，所述步骤s4包括：
[0086]
s41通过特征向量a
fast
和a
slow
分别构建两个矩阵a
slow
＝[a
fast a
slow
]和a
fast
＝[a
slow a
fast
]，并通过以下步骤求取两个辅助向量b
fast
和b
slow
：
[0087]
设a
fast
＝(x1,y1)，a
slow
＝(x2,y2)，x和y分别为向量的横纵坐标，计算x1y
2-x2y1的值。若x1y
2-x2y1的值小于0，则b
fast
＝(-y1,x1)，b
slow
＝(y2,-x1)；若x1y
2-x2y1的值大于0，则b
fast
＝(y1,-x1)，b
slow
＝(-y2,x1)；
[0088]
s42利用u
fast
、u
slow
、a
fast
、a
slow
、b
fast
、b
slow
得到恢复振幅和相位的快纵波波场和慢纵波波场其中θ
fast
＝[θ
solid_fast
θ
fluid_fast
]
t
，θ
slow
＝[θ
solid_slow
θ
fluid_slow
]
t
，θ
solid_fast
为固相快纵波，θ
fluid_fast
为液相快纵波，θ
solid_slow
为固相慢纵波，θ
fluid_slow
为液相慢纵波。
[0089]
将本实施例所提供的方法应用于层状模型中，可以得到较好的分离结果，图2为使用爆炸震源激发的地震波在双层的双相介质中传播的波场，可见快纵波、慢纵波以及横波耦合在一起，且波场较复杂，其中的横波是由快纵波和慢纵波遇到层界面转换产生。图3为实施步骤s1得到的纵波势波场和横波势波场，可以看出纵波和横波此时已经完全分离；但在纵波波场中，快纵波和慢纵波仍然耦合在一起。图4为实施步骤s3、s4后得到的分离并恢复了的快纵波波场和慢纵波波场，可以看到快纵波和慢纵波不仅完全分离，而且它们的振幅和相位也与图3中的纵波势波场相一致。图5为分离后的误差，可见误差非常小，分离结果很好。
[0090]
当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。