一种线性谐振马达谐振频率检测方法及系统与流程

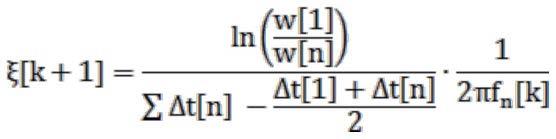
1.本发明实施例涉及线性谐振马达谐振频率检测技术领域，具体涉及一种线性谐振马达谐振频率检测方法及系统。


背景技术：

2.线性谐振马达(linear resonant actuator，lra)通常用于在便携终端上提供触觉反馈效果。lra包括弹簧、线圈和振子等构成部件。由lra驱动芯片提供驱动。驱动芯片在线圈上施加励磁电流，产生磁场，推动带有磁性的振子往某个方向移动。当励磁电流方向发生改变时，磁场和推动力也发生改变。因此，若在驱动芯片在线圈上施加周期电压信号，其产生的周期励磁电流，就会推动振子发生往返振动，达到触觉反馈的效果。由于lra的谐振特性，振子震动的幅度随驱动信号频率呈现带通特性，当驱动信号频率处于振子的固有频率(f0)时，振子震动的幅度达到最高，震动效率最佳。
3.在现有lra谐振频率检测中，驱动芯片在提供驱动电压波形中间关闭驱动信号，使lra振子自由震荡若干个周期，利用采集电路采集振子自有震荡时产生的感生电动势波形(back electromagnetic flux，bemf)。感生电动势波形是一阻尼震荡波形，通过对感生电动势波形的过零点间隔求平均，取倒数后计算出lra的阻尼震荡频率。
4.现有技术通过在驱动电压波形关闭时，检测bemf波形的过零点，对过零点间隔求平均后计算出lra的阻尼震荡频率。此方案有以下缺点：
5.(1)对bemf检测电路精度有较高要求，由于bemf波形为一阻尼震荡波形，随着周期数增加，bemf幅值会逐渐衰减至噪声门限以下，低信噪比下过零点检测会受噪声干扰而产生抖动，即使被平均几次，依然较难保证精度；
6.(2)二阶线性谐振系统的阻尼震荡频率与自由震荡频率之间存在的误差，ξ为马达阻尼系数，需要额外测出阻尼系数并进行校准才能得到自由振荡频率。


技术实现要素：

7.为此，本发明实施例提供一种线性谐振马达谐振频率检测方法及系统，以解决现有技术中的技术问题。
8.为了实现上述目的，本发明实施例提供如下技术方案：
9.根据本发明实施例的第一方面，本技术实施例提供了一种线性谐振马达谐振频率检测方法，所述方法包括：
10.通过驱动电路以预设频率播放若干个周期的波形，随后关闭所述驱动电路；
11.采集线性谐振马达两端电压波形，得到振子自由震荡时产生的感生电动势波形；
12.从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，其中，n为采样周期序号；
[0013]
利用所述峰值信号采集序列w[n]对所述过零信号时间间隔采集序列δt[n]进行
加权平均计算，得到加权平均过零时间
[0014]
利用所述加权平均过零时间峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，得到最终输出的线性谐振马达谐振频率。
[0015]
进一步地，利用所述加权平均过零时间峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，包括：
[0016]
将自由震荡阻尼系数初值ξ[0]赋为0，进行迭代运算；
[0017]
每次迭代运算完成后，判断所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]是否均满足各自的收敛条件；
[0018]
若所述自由震荡频率fn[k]或所述自由震荡阻尼系数ξ[k]不满足对应的收敛条件，则，令k＝k+1，进行下一次迭代运算；
[0019]
若所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]均满足对应的收敛条件，则迭代运算结束，将此时得到的自由震荡频率fn[k]作为最终输出的线性谐振马达谐振频率。
[0020]
进一步地，所述迭代运算的公式为：
[0021][0022][0023]
其中，k为迭代次数，k的初始值为0。
[0024]
进一步地，所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]的收敛条件分别为：
[0025][0026][0027]
其中，fn(lower_limit)为自由震荡频率fn[k]迭代运算收敛下限值，fn(upper_limit)为自由震荡频率fn[k]迭代运算收敛上限值，ξ[k](lower_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛下限值，ξ[k](upper_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛上限值。
[0028]
进一步地，所述加权平均过零时间的计算公式为：
[0029][0030]
其中，n为大于或等于1的整数。
[0031]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，包括：
[0032]
判断待测线性谐振马达的类型；
[0033]
如果待测线性谐振马达为对称类型线性谐振马达，则进入对称感生电动势波形检测模式；
[0034]
按照采样周期采集并记录下感生电动势波形中每个峰值电压的绝对值以及相邻两个异相过零点的时间间隔，其中，所述采样周期为所述感生电动势波形的变化周期的一半；
[0035]
每个所述采样周期采样完成后，判断记录的峰值电压的绝对值是否小于预设电压；
[0036]
若记录的峰值电压的绝对值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；
[0037]
若记录的峰值电压的绝对值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0038]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，还包括：
[0039]
如果待测线性谐振马达为非对称类型线性谐振马达，则进入非对称感生电动势波形检测模式；
[0040]
按照采样周期采集并记录下感生电动势波形中峰峰值以及相邻两个同相过零点的时间间隔，其中，所述采样周期等于所述感生电动势波形的变化周期；
[0041]
每个所述采样周期采样完成后，判断记录的峰峰值是否小于预设电压；
[0042]
若记录的峰峰值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；
[0043]
若记录的峰峰值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0044]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，还包括：
[0045]
若记录的峰值电压的绝对值或峰峰值未小于预设电压，则判断所述采样周期是否超出预设周期；
[0046]
若所述采样周期未超出预设周期，则进行下一个采样周期的采样；
[0047]
若所述采样周期超出预设周期，则立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0048]
进一步地，判断待测线性谐振马达的类型，包括：
[0049]
判断振子在正向和反向振动过程中速度大小是否相同以及方向是否相反；
[0050]
若振子在正向和反向振动过程中速度大小相同，且方向相反，则待测线性谐振马
达为对称类型线性谐振马达，上位机将模式选择信号设为0；
[0051]
若振子在正向和反向振动过程中速度大小不同，且方向相反，则待测线性谐振马达为非对称类型线性谐振马达，上位机将模式选择信号设为1。
[0052]
根据本发明实施例的第二方面，本技术实施例提供了一种线性谐振马达谐振频率检测系统，所述系统包括：
[0053]
驱动波形生成模块，用于通过驱动电路以预设频率播放若干个周期的波形，随后关闭所述驱动电路；
[0054]
驱动波形采集模块，用于采集线性谐振马达两端电压波形，得到振子自由震荡时产生的感生电动势波形；
[0055]
感生电动势波形检测模块，用于从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，其中，n为采样周期序号；
[0056]
加权平均过零时间计算模块，用于利用所述峰值信号采集序列w[n]对所述过零信号时间间隔采集序列δt[n]进行加权平均计算，得到加权平均过零时间
[0057]
迭代运算模块，用于利用所述加权平均过零时间峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，得到最终输出的线性谐振马达谐振频率。
[0058]
进一步地，利用所述加权平均过零时间对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，包括：
[0059]
将自由震荡阻尼系数初值ξ[0]赋为0，进行迭代运算；
[0060]
每次迭代运算完成后，判断所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]是否均满足各自的收敛条件；
[0061]
若所述自由震荡频率fn[k]或所述自由震荡阻尼系数ξ[k]不满足对应的收敛条件，则，令k＝k+1，进行下一次迭代运算；
[0062]
若所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]均满足对应的收敛条件，则迭代运算结束，将此时得到的自由震荡频率fn[k]作为最终输出的线性谐振马达谐振频率。
[0063]
进一步地，所述迭代运算的公式为：
[0064][0065][0066]
其中，k为迭代次数，k的初始值为0。
[0067]
进一步地，所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]的收敛条件分别为：
[0068][0069][0070]
其中，fn(lower_limit)为自由震荡频率fn[k]迭代运算收敛下限值，fn(upper_limit)为自由震荡频率fn[k]迭代运算收敛上限值，ξ[k](lower_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛下限值，ξ[k](upper_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛上限值。
[0071]
进一步地，所述加权平均过零时间的计算公式为：
[0072][0073]
其中，n为大于或等于1的整数。
[0074]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，包括：
[0075]
判断待测线性谐振马达的类型；
[0076]
如果待测线性谐振马达为对称类型线性谐振马达，则进入对称感生电动势波形检测模式；
[0077]
按照采样周期采集并记录下感生电动势波形中每个峰值电压的绝对值以及相邻两个异相过零点的时间间隔，其中，所述采样周期为所述感生电动势波形的变化周期的一半；
[0078]
每个所述采样周期采样完成后，判断记录的峰值电压的绝对值是否小于预设电压；
[0079]
若记录的峰值电压的绝对值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；
[0080]
若记录的峰值电压的绝对值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0081]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，还包括：
[0082]
如果待测线性谐振马达为非对称类型线性谐振马达，则进入非对称感生电动势波形检测模式；
[0083]
按照采样周期采集并记录下感生电动势波形中峰峰值以及相邻两个同相过零点的时间间隔，其中，所述采样周期等于所述感生电动势波形的变化周期；
[0084]
每个所述采样周期采样完成后，判断记录的峰峰值是否小于预设电压；
[0085]
若记录的峰峰值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；
[0086]
若记录的峰峰值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根
据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0087]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，还包括：
[0088]
若记录的峰值电压的绝对值或峰峰值未小于预设电压，则判断所述采样周期是否超出预设周期；
[0089]
若所述采样周期未超出预设周期，则进行下一个采样周期的采样；
[0090]
若所述采样周期超出预设周期，则立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0091]
进一步地，判断待测线性谐振马达的类型，包括：
[0092]
判断振子在正向和反向振动过程中速度大小是否相同以及方向是否相反；
[0093]
若振子在正向和反向振动过程中速度大小相同，且方向相反，则待测线性谐振马达为对称类型线性谐振马达，上位机将模式选择信号设为0；
[0094]
若振子在正向和反向振动过程中速度大小不同，且方向相反，则待测线性谐振马达为非对称类型线性谐振马达，上位机将模式选择信号设为1。
[0095]
与现有技术相比，本技术实施例提供的一种线性谐振马达谐振频率检测方法及系统，在驱动波形关闭期间，以较高采样率(48khz)同时对lra的bemf信号的峰值和过零时间进行采集。采用对过零点时间间隔加权平均的计算方法，以峰值或峰峰差值作为过零信号时间间隔采集序列的权重，进行加权平均，减小了低信噪比下bemf过零时间间隔的权重，可以有效改善低信噪比下bemf检测电路噪声对过零点抖动的影响，从而提高了线性谐振马达谐振频率检测精度。另外，自由震荡频率的计算考虑了阻尼系数的影响，在马达阻尼系数未知的条件下，通过对采集数据进行迭代运算，同时计算出马达的阻尼系数和自由震荡频率，达到了比现有技术更高的谐振马达谐振频率检测精度。
附图说明
[0096]
为了更清楚地说明本发明的实施方式或现有技术中的技术方案，下面将对实施方式或现有技术描述中所需要使用的附图作简单地介绍。显而易见地，下面描述中的附图仅仅是示例性的，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图引伸获得其它的实施附图。
[0097]
本说明书所绘示的结构、比例、大小等，均仅用以配合说明书所揭示的内容，以供熟悉此技术的人士了解与阅读，并非用以限定本发明可实施的限定条件，故不具技术上的实质意义，任何结构的修饰、比例关系的改变或大小的调整，在不影响本发明所能产生的功效及所能达成的目的下，均应仍落在本发明所揭示的技术内容得能涵盖的范围内。
[0098]
图1为本发明实施例提供的一种线性谐振马达谐振频率检测系统的结构示意图；
[0099]
图2为本发明实施例提供的一种线性谐振马达谐振频率检测方法的流程示意图；
[0100]
图3为本发明实施例提供的一种线性谐振马达谐振频率检测方法中对称感生电动势波形检测模式示意图；
[0101]
图4为本发明实施例提供的一种线性谐振马达谐振频率检测方法中非对称感生电动势波形检测模式示意图。
具体实施方式
[0102]
以下由特定的具体实施例说明本发明的实施方式，熟悉此技术的人士可由本说明书所揭露的内容轻易地了解本发明的其他优点及功效，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0103]
在现有检测方法中，驱动芯片在提供驱动电压波形中间关闭驱动信号，使lra振子自由震荡若干个周期，利用采集电路采集振子自有震荡时产生的bemf。bemf是一阻尼震荡波形，通过对感生电动势波形的过零点间隔求平均，取倒数后计算出lra的阻尼震荡频率。由于bemf波形为一阻尼震荡波形，随着周期数增加，bemf幅值会逐渐衰减至噪声门限以下，低信噪比下过零点检测会受噪声干扰而产生抖动，即使被平均几次，依然较难保证精度。
[0104]
为了解决上述技术问题，如图1所示，本技术实施例提供了一种线性谐振马达谐振频率检测系统包括：驱动波形生成模块01、驱动波形采集模块02、感生电动势波形检测模块03、加权平均过零时间计算模块04、迭代运算模块05。
[0105]
具体地，驱动波形生成模块01用于通过驱动电路06以预设频率播放若干个周期的波形，随后关闭驱动电路06；驱动波形采集模块02用于采集线性谐振马达07两端电压波形，得到振子自由震荡时产生的感生电动势波形并发送至感生电动势波形检测模块03；感生电动势波形检测模块03用于从感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]并发送至加权平均过零时间计算模块04，其中，n为采样周期序号；加权平均过零时间计算模块04用于利用峰值信号采集序列w[n]对过零信号时间间隔采集序列δt[n]进行加权平均计算，得到加权平均过零时间并发送至迭代运算模块05；迭代运算模块05用于利用加权平均过零时间峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，得到最终输出的线性谐振马达谐振频率。
[0106]
与现有技术相比，本技术实施例提供的一种线性谐振马达谐振频率检测系统，在驱动波形关闭期间，以较高采样率(48khz)同时对lra的bemf信号的峰值和过零时间进行采集。采用对过零点时间间隔加权平均的计算方法，以峰值或峰峰差值作为过零信号时间间隔采集序列的权重，进行加权平均，减小了低信噪比下bemf过零时间间隔的权重，可以有效改善低信噪比下bemf检测电路噪声对过零点抖动的影响，从而提高了线性谐振马达谐振频率检测精度。另外，自由震荡频率的计算考虑了阻尼系数的影响，在马达阻尼系数未知的条件下，通过对采集数据进行迭代运算，同时计算出马达的阻尼系数和自由震荡频率，达到了比现有技术更高的谐振马达谐振频率检测精度。
[0107]
与上述公开的一种线性谐振马达谐振频率检测系统相对应，本发明实施例还公开了一种线性谐振马达谐振频率检测方法。以下结合上述描述的一种线性谐振马达谐振频率检测系统详细介绍本发明实施例中公开的一种线性谐振马达谐振频率检测方法。
[0108]
如图2所示，本技术实施例提供了一种线性谐振马达谐振频率检测方法具体包括以下步骤。
[0109]
驱动波形生成模块01用于通过驱动电路06以预设频率播放若干个周期的波形，随后关闭驱动电路06。
[0110]
驱动波形采集模块02采集线性谐振马达07两端电压波形，得到振子自由震荡时产生的感生电动势波形并发送至感生电动势波形检测模块03。
[0111]
具体地，本发明实施例中的驱动波形采集模块02为模数转换电路(analog to digital converter)，当驱动电路06以预设的频率播放若干个周期的波形，随后关闭驱动波形后，即打开模数转换电路采集采集线性谐振马达07两端电压波形，即bemf波形。
[0112]
感生电动势波形检测模块03从感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]并发送至加权平均过零时间计算模块04，其中，n为采样周期序号。
[0113]
进一步地，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，包括：首先判断待测线性谐振马达的类型。具体地，判断待测线性谐振马达的类型，包括：判断振子在正向和反向振动过程中速度大小是否相同以及方向是否相反；若振子在正向和反向振动过程中速度大小相同，且方向相反，则待测线性谐振马达为对称类型线性谐振马达，上位机将模式选择信号设为0；若振子在正向和反向振动过程中速度大小不同，且方向相反，则待测线性谐振马达为非对称类型线性谐振马达，上位机将模式选择信号设为1。
[0114]
参考图3，如果待测线性谐振马达为对称类型线性谐振马达，因为模式选择信号为0，则感生电动势波形检测模块03进入对称感生电动势波形检测模式；按照采样周期采集并记录下感生电动势波形中每个峰值电压的绝对值以及相邻两个异相过零点的时间间隔，其中，所述采样周期为所述感生电动势波形的变化周期的一半；每个所述采样周期采样完成后，判断记录的峰值电压的绝对值是否小于预设电压；若记录的峰值电压的绝对值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；若记录的峰值电压的绝对值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0115]
参考图4，如果待测线性谐振马达为非对称类型线性谐振马达，因为模式选择信号为1，则感生电动势波形检测模块03进入非对称感生电动势波形检测模式；按照采样周期采集并记录下感生电动势波形中峰峰值以及相邻两个同相过零点的时间间隔，其中，所述采样周期等于所述感生电动势波形的变化周期；每个所述采样周期采样完成后，判断记录的峰峰值是否小于预设电压；若记录的峰峰值未小于预设电压，则判定线性谐振马达还处于震动状态，进行下一个采样周期的采样；若记录的峰峰值小于预设电压，则判定线性谐振马达停止震动，立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0116]
优选地，无论是对称感生电动势波形检测模式，还是非对称感生电动势波形检测模式，从所述感生电动势波形中检测出峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]，还包括：若记录的峰值电压的绝对值或峰峰值未小于预设电压，则判断所述采样周期是否超出预设周期；若所述采样周期未超出预设周期，则进行下一个采样周期的采样；若所述采样周期超出预设周期，则立即停止采集，根据记录信息生成所述峰值信号采集序列w[n]和所述过零信号时间间隔采集序列δt[n]。
[0117]
加权平均过零时间计算模块04利用峰值信号采集序列w[n]对过零信号时间间隔采集序列δt[n]进行加权平均计算，得到加权平均过零时间并发送至迭代运算模块05。
具体地，所述加权平均过零时间的计算公式为：
[0118][0119]
其中，n为大于或等于1的整数。
[0120]
本技术实施例中，在驱动波形关闭期间，以较高采样率(48khz)同时对lra的bemf信号的峰值和过零时间进行采集。采用对过零点时间间隔加权平均的计算方法，以峰值或峰峰差值作为过零信号时间间隔采集序列的权重，进行加权平均，减小了低信噪比下bemf过零时间间隔的权重，可以有效改善低信噪比下bemf检测电路噪声对过零点抖动的影响，从而提高了线性谐振马达谐振频率检测精度。
[0121]
迭代运算模块05利用加权平均过零时间峰值信号采集序列w[n]和过零信号时间间隔采集序列δt[n]对自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]进行迭代运算，得到最终输出的线性谐振马达谐振频率。进一步地，其具体包括：将自由震荡阻尼系数初值ξ[0]赋为0，进行迭代运算；所述迭代运算的公式为：
[0122][0123][0124]
其中，k为迭代次数，k的初始值为0。
[0125]
即，先利用自由震荡阻尼系数初值ξ[0]为0，计算自由震荡频率初值fn[0]，利用自由震荡频率初值fn[0]计算自由震荡阻尼系数初值ξ[1]，之后利用上述迭代运算的公式进行持续运算。
[0126]
每次迭代运算完成后，判断所述自由震荡频率fn[k]和所述自由震荡阻尼系数ξ[k]是否均满足各自的收敛条件。自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]的收敛条件分别为：
[0127][0128][0129]
其中，fn(lower_limit)为自由震荡频率fn[k]迭代运算收敛下限值，fn(upper_limit)为自由震荡频率fn[k]迭代运算收敛上限值，ξ[k](lower_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛下限值，ξ[k](upper_limit)为自由震荡阻尼系数ξ[k]迭代运算收敛上限值。
[0130]
若自由震荡频率fn[k]或自由震荡阻尼系数ξ[k]不满足对应的收敛条件，则，令k
＝k+1，进行下一次迭代运算；若自由震荡频率fn[k]和自由震荡阻尼系数ξ[k]均满足对应的收敛条件，则迭代运算结束，将此时得到的自由震荡频率fn[k]作为最终输出的线性谐振马达谐振频率。
[0131]
本技术实施例中，自由震荡频率的计算考虑了阻尼系数的影响，在马达阻尼系数未知的条件下，通过对采集数据进行迭代运算，同时计算出马达的阻尼系数和自由震荡频率，达到了比现有技术更高的谐振马达谐振频率检测精度。
[0132]
虽然，上文中已经用一般性说明及具体实施例对本发明作了详尽的描述，但在本发明基础上，可以对之作一些修改或改进，这对本领域技术人员而言是显而易见的。因此，在不偏离本发明精神的基础上所做的这些修改或改进，均属于本发明要求保护的范围。