一种氢气泄漏量测量方法及测量装置

1.本技术属于氢气应用技术领域，尤其涉及一种氢气泄漏量测量方法及测量装置。


背景技术：

2.氢气在进行存储时可能存在泄漏的危险，或者有时为了防止更大的危险发生，人们也会使用爆破片对储氢系统进行人工爆破，使得储氢系统中存储的氢气泄漏出来，减小储氢系统内的压力，以防止危险发生，并且氢气在泄漏到自然环境中时遇到明火可能发生危险，但是不同的泄漏量其遇到明火发生爆炸的范围也不一样，因此精确计算氢气的泄漏量至关重要。
3.但是，现有的氢气泄漏量计算模型复杂，且测量结果不准确。


技术实现要素：

4.有鉴于此，本技术实施例提供了一种氢气泄漏量测量方法及测量装置，能够解决现有的氢气泄漏计算模型复杂，且测量结果不准确的问题。
5.本技术实施例的第一方面提供了一种氢气泄漏量测量方法，所述氢气泄漏量测量方法包括：
6.计算储氢系统泄漏氢气的速度；其中，所述储氢系统泄漏氢气的速度分为第一阶段和第二阶段，从储氢系统开始泄漏氢气到泄漏口完全打开为第一阶段，从储氢系统的泄漏口完全打开到氢气停止泄漏为第二阶段，其中第一阶段需要的时间为t1，第一阶段和第二阶段共需要的时间为t2；
7.建立第一阶段泄漏口的面积变化模型a1；
[0008][0009]
其中，a0为泄漏口的初始泄漏面积，p1为储氢系统内的初始压强，p0为外界压强，t
(1)
为第一阶段内的任意时刻，e为泄漏口的有效弹性模量；
[0010]
根据第一阶段泄漏口的面积变化模型a1计算氢气在第一阶段的氢气泄漏速度v1；
[0011][0012]
其中，α为氢气的比热，m为氢气的摩尔质量，c为氢气的压缩因子，d 为气体常数，t为储氢系统内的温度；
[0013]
建立第二阶段储氢系统内压强变化模型
[0014]
根据第二阶段储氢系统内压强变化模型计算氢气在第二阶段的泄漏速度 v2；
[0015]
建立储氢系统的初始压强对氢气泄漏量的影响模型ζ；
[0016]
建立储氢系统氢气泄漏量的修正系数模型β；
[0017]
根据第一阶段氢气的泄漏速度、第二阶段氢气的泄漏速度以及储氢系统的初始压强对泄漏量的影响建立氢气的泄漏量q的数学模型，计算氢气的泄漏量 q。
[0018]
在一个实施例中，所述建立氢气的泄漏量q的数学模型为：
[0019][0020]
在一个实施例中，所述第一阶段需要的时间为t1，第一阶段和第二阶段共需要的时间为t2的测量方法为：
[0021]
在所述储氢系统周围设置至少一个计时传感器，所述至少一个计时传感器用于在所述储氢系统开始泄漏氢气时开始计时，在所述泄漏口完全打开不在增大时，输出时间t1，在所述储氢系统停止泄漏氢气时输出时间t2。
[0022]
在一个实施例中，所述建立第二阶段储氢系统内压强变化模型为：
[0023][0024]
其中，p1为储氢系统内的初始压强，ε1为初始压强随时间变化的比例系数，ε2为第二阶段储氢系统内压强变化的纠正因子，t
(2)
为第二阶段内的任意时刻。
[0025]
在一个实施例中，所述建立第二阶段储氢系统内压强变化模型为：
[0026]
其中，δ1为压强变化系数，δ2为压强比例系数，t
(2)
为第二阶段内的任意时刻。
[0027]
在一个实施例中，所述计算氢气在第二阶段的泄漏速度v2为：
[0028][0029]
其中，a
max
为泄漏口泄漏口完全打开的面积。
[0030]
在一个实施例中，所述泄漏口泄漏口完全打开的面积a
max
为：
[0031][0032]
其中，a0为泄漏口的初始泄漏面积，p1为储氢系统内的初始压强，p0为外界压强，t1为第一阶段需要的时间。
[0033]
在一个实施例中，所述建立储氢系统的初始压强对氢气泄漏量的影响模型ζ为：
[0034]
ζ＝λ1+λ2*cos(p1*λ4)+λ3*sin(p1*λ4)；
[0035]
其中，λ1为修正因子，λ2为余弦系数，λ3为正弦系数，λ4为初始压强的比例系数。
[0036]
在一个实施例中，所述建立储氢系统氢气泄漏量的修正系数模型β：
[0037]
其中，μ1为氢气泄漏量的指数系数，μ2为储氢系统内的初始压强的发展系数，μ3为氢气泄漏量的转换系数。
[0038]
本技术实施了的第二方面提供了一种测量装置，所述测量装置用于执行如上述任一项所述的氢气泄漏量测量方法。
[0039]
本技术实施例的有益效果是：通过提供一种氢气泄漏量测量方法，包括：计算储氢系统泄漏氢气的速度；其中，储氢系统泄漏氢气的速度分为第一阶段和第二阶段，从储氢系统开始泄漏氢气到泄漏口完全打开为第一阶段，从储氢系统的泄漏口完全打开到氢气停止泄漏为第二阶段，其中第一阶段需要的时间为t1，第一阶段和第二阶段共需要的时间为t2；然后建立第一阶段泄漏口的面积变化模型，根据第一阶段泄漏口的面积变化模型计算氢气在第一阶段的氢气泄漏速度；其次建立第二阶段储氢系统内压强变化模型，根据第二阶段储氢系统内压强变化模型计算氢气在第二阶段的泄漏速度，建立储氢系统的初始压强对氢气泄漏量的影响模型，建立储氢系统氢气泄漏量的修正系数模型，根据第一阶段氢气的泄漏速度、第二阶段氢气的泄漏速度以及储氢系统的初始压强对泄漏量的影响建立氢气的泄漏量的数学模型，计算氢气的泄漏量，本技术实施例通过将氢气泄漏速度分为两个阶段，并建立相应的数学模型，能够解决现有的氢气泄漏量计算模型复杂，且测量结果不准确的问题。
附图说明
[0040]
为了更清楚地说明本技术实施例中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本技术的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
[0041]
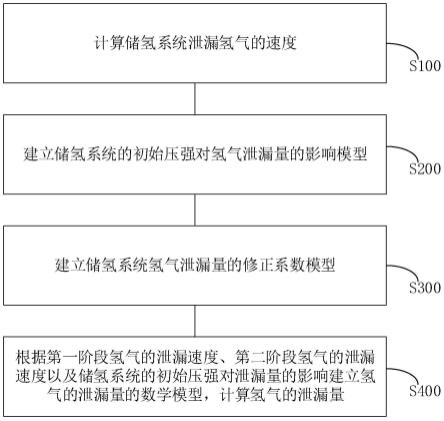
图1是本技术一个实施例提供的一种氢气泄漏量测量方法的步骤示意图；
[0042]
图2是本技术一个实施例提供地一种氢气泄漏量测量方法的具体步骤示意图；
[0043]
图3是本技术一个实施例提供的一种氢气泄漏量测量方法的结构示意图；
[0044]
图4是本技术一个实施例提供的一种氢气泄漏量测量方法的本专利方法与现有技术相比的误差率示意图。
具体实施方式
[0045]
以下描述中，为了说明而不是为了限定，提出了诸如特定系统结构、技术之类的具体细节，以便透彻理解本技术实施例。然而，本领域的技术人员应当清楚，在没有这些具体细节的其它实施例中也可以实现本技术。在其它情况中，省略对众所周知的系统、装置、电路以及方法的详细说明，以免不必要的细节妨碍本技术的描述。
[0046]
下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行清楚地描述，显然，所描述的实施例是本技术一部分实施例，而不是全部的实施例。基于本技术中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本技术保护的范围。
[0047]
氢气在进行存储时可能存在泄漏的危险，或者有事为了防止更大的危险发生，人们也会使用爆破片对储氢系统进行人工爆破，使得储氢系统中存储的氢气泄漏出来，减小储氢系统内的压力，以防止危险发生，并且氢气在泄漏到自然环境中时遇到明火可能发生危险，但是不同的泄漏量其遇到明火发生爆炸的范围也不一样，因此精确计算氢气的泄漏
量至关重要。
[0048]
但是，现有的氢气泄漏量计算模型复杂，且测量结果不准确。
[0049]
为了解决上述技术问题，本技术实施例提供了一种氢气泄漏量测量方法，参考图1、图2、图3所示，其中，氢气泄漏量测量方法包括：步骤s100至步骤s400。
[0050]
具体的，步骤s100，计算储氢系统泄漏氢气的速度；其中，储氢系统泄漏氢气的速度分为第一阶段和第二阶段，从储氢系统开始泄漏氢气到泄漏口完全打开为第一阶段，从储氢系统的泄漏口完全打开到氢气停止泄漏为第二阶段，其中第一阶段需要的时间为t1，第一阶段和第二阶段共需要的时间为t2；
[0051]
步骤s110：建立第一阶段泄漏口的面积变化模型a1；
[0052][0053]
其中，a0为泄漏口的初始泄漏面积，p1为储氢系统内的初始压强，p0为外界压强，t
(1)
为第一阶段内的任意时刻，e为泄漏口的有效弹性模量，t1为泄漏口的初始泄漏面积a0到泄漏口完全打开所需要的时间，此时储氢系统内压强基本不变。
[0054]
步骤s120：根据第一阶段泄漏口的面积变化模型a1计算氢气在第一阶段的氢气泄漏速度v1；(0《t《t1)
[0055][0056]
其中，α为氢气的比热，m为氢气的摩尔质量，c为氢气的压缩因子，d 为气体常数，t为储氢系统内的温度；
[0057]
步骤s130：建立第二阶段储氢系统内压强变化模型
[0058]
步骤s140：根据第二阶段储氢系统内压强变化模型计算氢气在第二阶段的泄漏速度v2；
[0059]
步骤s200：建立储氢系统的初始压强对氢气泄漏量的影响模型ζ；
[0060]
步骤s300：建立储氢系统氢气泄漏量的修正系数模型β；
[0061]
步骤s400：根据第一阶段氢气的泄漏速度、第二阶段氢气的泄漏速度以及储氢系统的初始压强对泄漏量的影响建立氢气的泄漏量q的数学模型，计算氢气的泄漏量q。
[0062]
在本实施例中，在步骤s100中，储氢系统可以是高压储氢罐、地下储氢空间或者是管道储氢等储氢形式。将储氢系统泄漏氢气的速度分为第一阶段和第二阶段，可以理解的是，储氢系统在开始泄漏时，泄漏氢气的口称之为泄漏口，泄漏口在开始泄漏时面积很小，随着泄漏时间的增加以及储氢系统内外压差的影响，使得泄漏口逐渐增大，当增加到一定程度时，不再增大，当开始出现泄漏口到泄漏口完全打开时为第一阶段，第一阶段可以通过传感器检测泄漏口的面积大小进行判断，在第一阶段：从储氢系统开始泄漏氢气到泄漏口完全打开经历的时间t1很短，在第一阶段氢气的泄漏速度逐渐增大，此时速度增大的主要原因是泄漏口逐渐增大导致的，因为第一阶段的时间t1很短，所以此时储氢系统中的压强基本保持不变，按照定值计算。
[0063]
在本实施例中，在步骤s100中，从储氢系统的泄漏口完全打开到氢气停止泄漏为
第二阶段。第一阶段与第二阶段的总时间t2同样通过传感器检测得到，可以理解的是，当传感器检测到储氢系统开始泄漏氢气时开始计时，并在检测到泄漏口不再增大，即视为完全打开，即泄漏口打开到最大，此时输出时间t1，并继续计时，并在检测到储氢系统不再泄漏氢气或者氢气泄漏完后停止计时，并输出总时间t2，则第二阶段的时间为t
1-t2。
[0064]
在本实施例中，第二阶段泄漏氢气时，泄漏口的面积已经达到最大，可以理解的是，泄漏口的面积已经完全打开，在第二阶段氢气的泄漏速度是先增大再减小，即泄漏速度的加速度是先增大再减小的，此时，泄漏口面积完全打开为a
max
，此时储氢系统中的压强是逐渐减小的，直到储氢系统中的压强与外界压强相等才停止泄漏，或者可以理解氢气泄漏完成。
[0065]
在本实施例中，在步骤s110中，建立第一阶段泄漏口的面积变化模型a1，可以理解的是，在第一阶段泄漏口的面积是在很短的时间内逐渐增大的，即在第一阶段泄漏口的面积一直是变化的，这就需要建议泄漏口面积变化模型a1，随时计算第一阶段泄漏口的面积大小，并且第一阶段的泄漏口的面积与泄漏口的有效弹性模量有关，不同材料的弹性模量也不相同，其中，泄漏口的面积与弹性模量呈反比，泄漏口的有效弹性模量可以为泄漏口的弹性模量的平均值。可以理解的是，a1并不是一个固定值，t
(1)
是第一阶段内的任意时刻，即，可以理解的是，t
(1)
的范围是：(0＜t
(1)
≤t1)，即t
(1)
可以是0到t1内的任意值，t
(1)
不同时，则对应的a1就表示此时泄漏口的面积大小，通过建立第一阶段泄漏口的面积变化模型a1可以实时得到第一阶段泄漏口的面积大小，通过第一阶段泄漏口的面积变化模型计算第一阶段的氢气泄漏速度。
[0066]
在本实施例中，在步骤s120中，根据第一阶段泄漏口的面积变化模型a1计算氢气在第一阶段的氢气泄漏速度v1；
[0067][0068]
其中，α为氢气的比热，m为氢气的摩尔质量，c为氢气的压缩因子，d 为气体常数，t为储氢系统内的温度；在本实施例中，v1对应的是第一阶段的氢气泄漏速度，可以理解的是，不同的时间t
(1)
对应的泄漏口的面积a1是不相同的，不同的泄漏口面积a1对应的第一阶段的泄漏速度v1是不相同的，通过变化的泄漏口的面积计算第一阶段的泄漏速度可以使得计算结果更加准确，能够解决现有的氢气泄漏计算模型复杂，且测量结果不准确的问题。
[0069]
在一个实施例中，氢气的比热采用14300j/(kg
·
k)，氢气的摩尔质量2g/mol，气体常数为8.314j/(mol
·
k)，氢气的压缩因子与储氢系统的压强和温度有关，上述参数一般可以通过物性参数表查的，在此不再赘述。
[0070]
在本实施例中，在步骤s130中，建立第二阶段储氢系统内压强变化模型
[0071]
具体的，建立第二阶段储氢系统内压强变化模型为：
[0072][0073]
其中，p1为储氢系统内的初始压强，ε1为初始压强随时间变化的比例系数，ε2为第二阶段储氢系统内压强变化的纠正因子，t
(2)
为第二阶段内的任意时刻。在本实施例中，在
第二阶段中，储氢系统中的压强是一直变化的，并且压强跟第二阶段中的时间t
(2)-t1有关，t
(2)
为大于第一阶段的时间t1的值，位于第二阶段内的时间，可以理解的是，t
(2)
的取值范围是t1＜t
(2)
≤t2，通过设定第二阶段内压强变化计算第二阶段的氢气泄漏速度，可以使得计算结果更加准确，能够解决现有的氢气泄漏计算模型复杂，且测量结果不准确的问题。
[0074]
在一个实施例中，出初始压强p1为7.4mpa，初始压强随时间变化的比例系数ε1为0.56，第二阶段储氢系统内压强变化的纠正因子ε2为1.86，分别计算在1秒、1.5秒、2秒、3秒、4秒、5秒、7秒、10秒计算第二阶段储氢系统内压强变化模型分别为：6.6mpa、4.8mpa、3.7mpa、2.8mpa、2mpa、1.7mpa、 1.3mpa、1mpa，直到21秒时接近0mpa。
[0075]
在本实施例中，在步骤s140中，根据第二阶段储氢系统内压强变化模型计算氢气在第二阶段的泄漏速度v2。
[0076]
具体的，计算氢气在第二阶段的泄漏速度v2，通过建立泄漏速度v2的数学模型为：
[0077][0078]
其中，a
max
为泄漏口泄漏口完全打开的面积。
[0079]
在本实施例中，可以理解的是，第二阶段的泄漏速度v2是时刻在发生变化的，其与储氢罐内的压强有关，即，储氢罐中的压强不同时，对应的第二阶段的泄漏速度v2是不相同的，可以理解的是，在第二阶段泄漏口的面积是保持不变的，即一直保持a
max
不变，此时的面积是泄漏口完全打开，即泄漏口面积最大，通过设置第二阶段的泄漏速度随着储氢罐中的压强变化而变化，可以使得氢气泄漏量的计算更加准确，能够解决现有的氢气泄漏计算模型复杂，且测量结果不准确的问题。
[0080]
在本实施例中，在步骤s200中，建立储氢系统的初始压强对氢气泄漏量的影响模型ζ。
[0081]
具体的，建立储氢系统的初始压强对氢气泄漏量的影响模型ζ为：
[0082]
ζ＝λ1+λ2*cos(p1*λ4)+λ3*sin(p1*λ4)；
[0083]
其中，λ1为修正因子，λ2为余弦系数，λ3为正弦系数，λ4为初始压强的比例系数。
[0084]
具体的，不同的储氢系统的初始压强对氢气的泄漏量也有影响，通过设置建立储氢系统的初始压强对氢气泄漏量的影响模型ζ可以使得储氢系统的氢气泄漏量计算结果更加准确。在一个实施例中，修正因子λ1为2.80，余弦系数λ2为
ꢀ‑
2.69，正弦系数λ3为1.82，初始压强的比例系数λ4为0.15。在一个实施例中，初始压强分别为9.52mpa、8.45mpa、7.38mpa、6.12mpa、4.9mpa、4.09mpa、 3.3mpa对氢气泄漏量的影响模型ζ分别为0.42kg、0.38kg、0.33kg、0.26kg、 0.20kg、0.16kg、0.12kg，通过建立储氢系统的初始压强对氢气泄漏量的影响模型ζ可以使得氢气泄漏量计算更加准确。
[0085]
在本实施例中，在步骤s300中，建立储氢系统氢气泄漏量的修正系数模型β。建立储氢系统氢气泄漏量的修正系数模型β：
[0086]
其中，μ1为氢气泄漏量的指数系数，μ2为储氢系统内的初始压强的发展系数，μ3为氢气泄漏量的转换系数。
[0087]
在本实施例中，氢气泄漏量的指数系数μ1为4858，储氢系统内的初始压强的发展系数μ2为23.24，氢气泄漏量的转换系数μ3为15.37，通过储氢系统氢气泄漏量的修正系数模型β可以对储氢罐中氢气泄漏量进行修正。
[0088]
在本实施例中，在步骤s400中，根据第一阶段氢气的泄漏速度、第二阶段氢气的泄漏速度以及储氢系统的初始压强对泄漏量的影响建立氢气的泄漏量 q的数学模型，计算氢气的泄漏量q。
[0089]
具体的，建立氢气的泄漏量q的数学模型为：
[0090]
通过将第一阶段氢气的泄漏速度v1、第二阶段氢气的泄漏速度v2；进行积分处理，然后加上储氢系统的初始压强对氢气泄漏量的影响模型ζ和储氢系统氢气泄漏量的修正系数模型β；可以准确的计算出储氢罐中氢气的泄漏量，其中t2可以进行更换不一定非要计算泄露完成时的氢气泄漏量，可以计算任意时刻的氢气的泄漏量。
[0091]
在一个实施例中，第一阶段需要的时间为t1，第一阶段和第二阶段共需要的时间为t2的测量方法为：
[0092]
在储氢系统周围设置至少一个计时传感器，至少一个计时传感器用于在储氢系统开始泄漏氢气时开始计时，在泄漏口完全打开不在增大时，输出时间t1，在储氢系统停止泄漏氢气时输出时间t2。
[0093]
在一个实施例中，建立第二阶段储氢系统内压强变化模型还可以为：
[0094][0095]
其中，δ1为压强变化系数，δ2为压强比例系数，t
(2)
为第二阶段内的任意时刻。
[0096]
在本实施例中，压强变化系数δ1为14.98，压强比例系数δ2为1.89，t
(2)
为第二阶段内的任意时刻。
[0097]
在一个实施例中，泄漏口泄漏口完全打开的面积a
max
为：
[0098][0099]
其中，a0为泄漏口的初始泄漏面积，p1为储氢系统内的初始压强，p0为外界压强，t1为泄漏口的初始泄漏面积a0到泄漏口完全打开所需要的时间，即t1为第一阶段需要的时间。
[0100]
在一个实施例中，如图4所示，采用本专利方法在不同地下储氢气空间中进行了15次速度测量实验，由图可知采用本专利方法测量地下储氢气空间速度的平均误差值为1.48％，方差为1.79，最大误差为1.41％，故本专利方法稳定。采用本专利方法在不同地下储氢气空间中进行了15次速度测量实验，并将平均值作为结果记录，比现有测量方法准确。
[0101]
本技术实施例还提供了一种测量装置，所述测量装置用于执行如上述任一项所述的氢气泄漏量测量方法。
[0102]
在上述实施例中，对各个实施例的描述都各有侧重，某个实施例中没有详述或记载的部分，可以参见其它实施例的相关描述。
[0103]
以上实施例仅用以说明本技术的技术方案，而非对其限制；尽管参照前述实施例对本技术进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本技术各实施例技术方案的精神和范围，均应包含在本技术的保护范围之内。