基于移动节点的纯方位目标定位方法

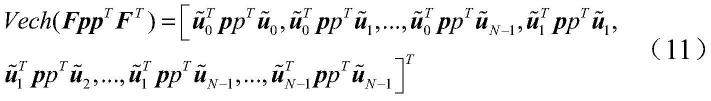
1.本发明属于目标定位技术领域，具体涉及一种基于移动节点的纯方位目标定位方法。


背景技术：

2.基于到达角(angle-of-arrival，aoa)量测信息的目标定位方法在无线传感器网络、航空航天电子系统和自动控制等民用和军事领域获得了广泛应用，因此几十年来吸引了大量学者对此进行研究。aoa量测信息通常由传感器对目标发出的信号监听获得。在二维平面上，利用单个移动传感器测量的aoa信息能够估计出目标位置。移动传感器可以是无人机或无人水下航行器。
3.从估计理论的角度来看，aoa定位是一个非线性估计问题，其主要挑战来自aoa量测值与真实目标位置之间的高度非线性关系。目前的主流方法有网格搜索法、最大似然估计方法、闭式伪线性估计方法等。网格搜索法通过搜索所有可能的目标位置来获得测量的最佳拟合，计算耗时。最大似然估计方法具有渐近无偏性和有效性，但是通常需要搜索方法(如最速下降算法、高斯—牛顿迭代算法)获得估计值，计算复杂度高。除此之外，当初始值设置不合理时，最大似然估计方法的估计性能会不稳定。
4.闭式伪线性估计方法通常构造一个线性最小二乘估计器，可以获得闭式解，因此计算量较小。但是由于测量矩阵和伪线性噪声向量之间的相关性，当量测噪声较大时，估计精度会严重下降。为了提高估计精度，学者们基于线性最小二乘估计器，提出许多改进方法，如偏差补偿方法、加权辅助变量估计方法、加权最小二乘估计方法等。这些改进方法需要测量噪声的统计信息(例如方差)作为先验信息，来计算偏差补偿或加权矩阵。然而，在实际工程中，先验信息通常需要估计获得。一方面，估计先验信息会增加系统的复杂性；另一方面，先验信息的估计误差较大时，偏差补偿或加权矩阵也会含有较大噪声，对目标定位精度造成不利影响，难以满足定位需求。


技术实现要素：

5.本发明的目的在于提供一种基于移动节点的纯方位目标定位方法，不仅可以得到闭式解，计算量低；而且能够有效提高定位精度，稳定性较好。
6.本发明所采用的技术方案是：基于移动节点的纯方位目标定位方法，包括以下步骤：
7.步骤1、基于目标信号的真实aoa值非线性函数和aoa量测噪声建立aoa量测值模型，aoa量测噪声为零均值、方差与目标-节点距离相关的加性高斯白噪声；
8.步骤2、将步骤1所得aoa量测值代入步骤1中的真实aoa值非线性函数得到伪线性方程，通过最小二乘法求解得到目标估计位置；
9.步骤3、使用步骤2所得目标估计位置计算得到aoa估计值，建立辅助变量矩阵，利用辅助变量估计方法得到新的目标估计位置；
10.步骤4、计算步骤2中伪线性方程的二阶表达式并将其展开成向量形式，再将向量形式与步骤2中的伪线性方程联立，得到广义伪线性方程组；
11.步骤5、利用泰勒级数展开公式，将步骤4所得广义伪线性方程组改写成新的伪线性方程，基于步骤3所得新的目标估计位置建立并引入新的辅助变量矩阵，得到目标定位估计值。
12.本发明的特点还在于，
13.步骤1具体为：在时刻k∈{0,1,2,...,n-1}，目标信号的真实aoa值θk为：
[0014][0015]
式(1)中，rk＝[xk,yk]
t
是移动节点在时刻k的位置，p＝[p
x
,py]
t
为目标位置，函数f(.,.)表示θk与目标和节点位置之间的非线性关系；
[0016]
通过移动节点对目标进行观测，得到的aoa量测值为：
[0017][0018]
式(2)中，nk是aoa量测噪声，为零均值、方差的加性高斯白噪声，即方差与信噪比有关，而信噪比与目标-节点之间的距离有关，因此将方差建模为与距离相关的函数：
[0019][0020]
式(3)中，dk表示时刻k时目标到节点的距离，α是路径损耗指数，d0是参考距离，设置d0＝1，表示d0处aoa量测噪声的方差。
[0021]
步骤2具体为：将aoa量测值代入公式(1)得到如下伪线性方程：
[0022]
f p＝b+η
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0023]
式(4)中，f为测量矩阵，通过如下公式(5a)表示；b为测量向量，通过如下公式(5b)表示；η为噪声向量，通过如下公式(5c)表示：
[0024][0025][0026]
η＝[η0,η1,...,η
n-1
]
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5c)
[0027]
式(5a)和(5b)中，uk通过如下公式(5d)表示：
[0028][0029]
通过最小二乘法求解得到目标估计位置：
[0030][0031]
式(6)中，上标
t
表示矩阵的转置操作。
[0032]
步骤3的具体步骤为：
[0033]
步骤3.1、将步骤2所得目标估计位置代入公式(1)计算得到aoa估计值
[0034]
步骤3.2、基于步骤3.1所得建立辅助变量矩阵h：
[0035][0036]
步骤3.3、用h
t
替换公式(6)中的测量矩阵f
t
，得到新的目标估计位置：
[0037][0038]
步骤4具体为：计算伪线性方程即公式(4)的二阶表达式：
[0039]
bb
t
＝(fp-η)(fp-η)
t
＝fpp
tft
+γ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0040]
式(9)中，γ＝ηη
t-fpη
t-ηp
tft
表示噪声项，将公式(9)写成向量形式：
[0041]
vech(bb
t
)＝vech(fpp
tft
)+vech(γ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0042]
式(10)中，vech(fpp
tft
)是大小为n(n+1)/2
×
1的向量，里面的元素为：
[0043][0044][0045]
将公式(4)与公式(10)联立，得到一组广义伪线性方程：
[0046][0047]
式(13)中，a(p)表示p的二次函数，ε是噪声项。
[0048]
步骤5具体为：借助于一阶泰勒级数展开式，将公式(13)在处进行线性化展开，结果如下：
[0049][0050]
式(14)中，是将a(p)中的p替换为计算得出的，由下式给出：
[0051][0052]
[0053][0054]
经过代数运算后，公式(14)变为新的伪线性方程：
[0055][0056]
式(18)中，g是测量矩阵，是数据向量，-ε是伪线性噪声向量；
[0057]
使用公式(7)中新的目标估计位置带入公式(1)计算得到新的aoa估计值并由构建一个新的辅助变量矩阵将公式(18)等号左右两边同时乘以d
t
，并用d替换等号右边的g，忽略噪声项，得到：
[0058][0059]
求解得到目标定位估计值：
[0060][0061]
本发明的有益效果是：本发明的基于移动节点的纯方位目标定位方法，基于距离相关噪声模型，通过对最小二乘估计方法进行改进，可以获得闭式解，避免了迭代的复杂计算；同时不需要量测噪声的先验信息，避免增加系统的复杂性。并且，本发明通过构建广义伪线性方程，引入辅助变量矩阵，可以有效提升目标定位的精度和稳定性。
附图说明
[0062]
图1是本发明中基于aoa的移动节点目标定位场景；
[0063]
图2是模拟定位场景；
[0064]
图3是是0.04
°
≤σ
θ
≤0.22
°
时最大似然估计、最小二乘法、辅助变量法和本发明方法的偏差范数关系曲线；
[0065]
图4是0.04
°
≤σ
θ
≤0.22
°
时最大似然估计、最小二乘法、辅助变量法和本发明方法的均方误差关系曲线。
具体实施方式
[0066]
下面结合附图以及具体实施方式对本发明进行详细说明。
[0067]
本发明提供了一种基于移动节点的纯方位目标定位方法，具体步骤如下：
[0068]
步骤1，建立噪声模型；
[0069]
在aoa定位问题中，目标位置未知，需要对其进行估计。如图1所示，在时刻k∈{0,1,2,...,n-1}，目标信号的真实aoa值θk为：
[0070][0071]
其中，rk＝[xk,yk]
t
是移动节点在时刻k的位置，p＝[p
x
,py]
t
为目标位置，θk为在时刻k静止目标p与节点rk的方向角，函数f(.,.)表示θk与目标和节点位置之间的非线性关系。在实际工程中，真实aoa值是未知的。通过移动节点对目标进行观测，得到的aoa量测值
为：
[0072][0073]
其中，nk是aoa量测噪声，建模为零均值、方差的独立高斯白噪声，即本发明中，设定的先验知识是未知的。
[0074]
aoa噪声方差与信噪比有关，而信噪比与目标-节点之间的距离有关。因此，将建模为与距离相关的函数：
[0075][0076]
其中，dk表示时刻k时目标到节点的距离，α是路径损耗指数，d0是参考距离(本发明中，设置d0＝1)，表示d0处aoa量测噪声的方差。
[0077]
步骤2，构建线性最小二乘估计器；
[0078]
利用建立的aoa目标定位模型，推导出线性最小二乘估计的目标位置。将aoa量测值代入公式(1)，进行整理后，可以得到如下伪线性方程：
[0079]
f p＝b+η
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0080]
其中，
[0081][0082][0083]
η＝[η0,η1,...,η
n-1
]
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5c)
[0084][0085]
利用最小二乘估计方法，可以得到目标估计位置：
[0086][0087]
该最小二乘求解结果被称为最小二乘估计器，其中b为测量向量，上标
t
表示矩阵的转置操作。
[0088]
步骤3，构建辅助变量估计器；
[0089]
由于测量矩阵f和噪声向量η之间的相关性，最小二乘估计器是有偏差的。为了减少偏差，建立辅助变量矩阵h，用h
t
去替换测量矩阵f
t
。因此，伪线性方程f
t
f p＝f
t
b被修改为新的正规方程h
t
f p＝h
t
b，从而得到辅助变量估计器。其目标位置估计结果如下
[0090][0091]
其中，辅助变量矩阵h由aoa估计值来构造，即：
[0092][0093]
其中，aoa估计值是将公式(6)的代入公式(1)计算得到的，即
[0094]
步骤4，构建广义伪线性方程组；
[0095]
尽管辅助变量估计器的精度优于最小二乘估计器，但当测量噪声较大时，仍然具有一定的偏差。为了进一步提高定位性能，本发明构建了一组广义伪线性方程。首先，计算伪线性方程(4)的二阶表达式：
[0096]
bb
t
＝(fp-η)(fp-η)
t
＝fpp
tft
+γ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0097]
式中，γ＝ηη
t-fpη
t-ηp
tft
表示噪声项。由于bb
t
和fpp
tft
都是对称矩阵，所以只考虑(9)中矩阵的对角元素和下对角元素。因此，可将式(9)写成向量形式
[0098]
vech(bb
t
)＝vech(fpp
tft
)+vech(γ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0099]
其中，vech(fpp
tft
)是大小为n(n+1)/2
×
1的向量，里面的元素为
[0100][0101][0102]
将公式(4)与公式(10)相结合，得到一组广义伪线性方程
[0103][0104]
其中a(p)表示p的二次函数，ε是噪声项。
[0105]
步骤5，引入辅助变量矩阵，得到目标位置。
[0106]
借助于一阶泰勒级数展开式，将公式(13)在处进行线性化展开，结果如下：
[0107][0108]
其中，是将a(p)中的p替换为计算得出的，由下式给出：
[0109][0110][0111]
[0112]
经过代数运算后，公式(14)变为
[0113][0114]
上述方程可视为一种新的伪线性方程，其中g是测量矩阵，是数据向量，-ε是伪线性噪声向量。
[0115]
使用公式(7)中的带入公式(1)计算得到新的aoa估计值并由此估计值构建一个新的辅助变量矩阵将公式(18)等号左右两边同时乘以d
t
，并用d替换等号右边中的g，忽略噪声项，得到
[0116][0117]
因此，得到一个新的闭式解，
[0118][0119]
利用公式(20)计算的结果为本发明提出的目标定位估计值。
[0120]
性能分析
[0121]
采用蒙特卡罗模拟统计方法，将提出的本发明方法算法的定位性能与最小二乘算法、辅助变量算法和最大似然估计算法进行了比较。其中，最大似然估计的迭代次数指定为k＝10。使用估计误差和均方误差作为精度衡量标，作为性能比较的依据。估计误差和均方误差分别由以下公式计算：
[0122][0123][0124]
其中，表示第i次蒙特卡罗试验中p的估计值，m＝2000表示蒙特卡罗试验的次数。在模拟场景中，假设目标位于[25,300]
t
，移动节点沿着py＝0.8p
x
+10线性路径移动。当5≤p
x
≤35和k＝0,1,...,49时，模拟定位场景如图2所示，其中三角形代表移动节点运动的轨迹，圆形代表静止目标的位置。
[0125]
当σ
θ
从0.04
°
增加至0.22
°
且步长为0.03
°
时，四个估计器的偏差范数结果如图3所示。在四个估计量中，最小二乘法表现出最大的误差，说明其存在严重的偏差问题。虽然辅助变量法与最小二乘法相比减少了偏差，但它仍然比本发明方法有更大的偏差。对于σ
θ
≤0.19
°
最大似然估计的偏差小于最小二乘法的偏差，但对于较大的aoa噪声(例如σ
θ
》0.22
°
)，最大似然估计的误差会迅速增加。这一观察结果表明了最大似然估计方法具有发散问题。由于本发明方法利用构建的广义伪线性方程组，能够利用更多的信息，并且借用辅助变量方法的优势，因此本发明方法优于其他估计器。
[0126]
图4比较了不同σ
θ
值下最大似然估计、最小二乘法、辅助变量法和本发明方法的均方误差性能。当σ
θ
≤0.19
°
时，最小二乘法不如其它三种估计。与最小二乘法相比，最大似然估计和辅助变量法具有更小的均方误差。然而，当σ
θ
大于0.19
°
时，辅助变量法的均方误差变得非常大。这一观察结果表明，对于较大的aoa噪声，辅助变量法的均方误差性能变得不稳定。此外，当σ
θ
》0.19
°
时，最大似然估计的均方误差会出估计结果发散的问题。在四种估
计方法中，本发明方法表现出优越的目标定位性能。