一种三维激光扫描系统的自校准方法

1.本发明属于三维激光扫描技术领域，特别涉及一种三维激光扫描系统的自校准方法。


背景技术：

2.三维激光扫描技术，也称“实景复制”技术，是一种无接触的空间数据快速获取技术。与传统的测量方式相比，三维扫描具有数据获取速度快，实时性强，主动性强，数据量大，能全天候工作，全数字特征，信息传输、处理、表达容易，操作方便等优点。一方面，三维扫描系统在搭建时各部分存在加工和装配误差，另一方面，由于激光扫描设备出现较晚，结构相对复杂，缺乏对应的检定标准与校准规范，导致难以对其测量数据质量进行有效控制。
3.目前三维激光扫描系统的校准方法大都采用标准模板法，即通过标准模板上三维坐标已知的被测点将扫描系统坐标系和测量基准坐标系联系起来，进而求得两个坐标系间的变换方程。比如文献“rondeel s.calibration,validation,and verification of static terrestrial laser scanning forprofessional land surveying of3d boundaries”用莱卡全站仪对地面三维激光扫描仪的测量结果进行校准，验证了激光扫描测量结果的精度。这类方法通常需要借助额外的已标定好测量仪器(例如激光跟踪仪、全站仪等)及其标靶，提前确定被测点及扫描系统的准确位置；并且，由于扫描测距系统的激光脉冲是不可见的、而且扫描点是离散的，因此被测点在扫描系统坐标系内的三维坐标难于精确获得。
4.近年来，一些学者尝试无测量仪器的三维测量装置标定方法，例如专利cn 112179291a“一种自旋转扫描式线结构光三维测量装置标定方法”借助平面靶标，基于各组平面靶标在自旋转扫描式线结构光三维测量装置下的三维数据分别满足平面约束的条件，采用最小二乘法拟合各平面，实现对线结构光轮廓测量仪的坐标系和三维测量装置的坐标系之间位置参数的标定，该方法对于影响扫描目标形状的参数误差有较好的标定效果，但无法补偿影响扫描目标整体位置偏差的参数误差。


技术实现要素：

5.本发明提出了一种新的激光扫描系统校准方法，其目的在于克服三维激光扫描系统校准过程中对其它测量仪器的依赖，简化校准流程，补偿三维扫描系统各测量参数误差，提高扫描精度。首先，明确扫描系统测量参数与各测点坐标直接的关系，根据扫描设备相关的测量参数，如采样点密度、扫描范围等，准备一块尺寸合适且已知的方块；然后用待校准的扫描设备扫描该方块，在扫描方块得到的点云中，分离出方块顶点坐标，建立方块顶点之间的测量距离与扫描系统参数的关系；最后通过优化算法来找到一个合适的扫描系统参数校准值，使得方块顶点测量距离与方块实际边长最接近。校准过程无需额外的测量仪器，借助边长已知的方块作为标定物，避免了其他测量仪器本身的测量误差、标靶加工及安装带来的累计误差。
6.为达到上述目的，本发明采用如下技术方案：
7.步骤1：确定激光扫描系统的测量模型，根据扫描系统采样点密度、扫描范围，准备一块边长为l的正方体方块作为标定物。
8.步骤2：将方块置于扫描系统的扫描范围内进行扫测，方块与扫描系统底座处于同一平面，分离出方块4个顶点坐标及对应的测量参数。
9.步骤3：建立扫描校准模型，计算4个顶点对应的误差转换矩阵。
10.步骤4：通过最小二乘法优化求解出各测量参数修正量，对测量模型进行修正。
11.步骤5：重复步骤3、步骤4，直到距离测算误差在容许值内，输出更新后的测量模型。
12.使用上述一种三维激光扫描系统的自校准方法，对线激光与旋转云台搭建的三维激光扫描系统进行个测量参数的校准，与现有技术相比能够得到以下有益效果：
13.本发明借助一尺寸已知的方块进行校准，校准过程无需借助其他测量设备，简化校准流程，有效补偿三维扫描系统各参数测量误差，保证扫描各点坐标测量精度。
附图说明
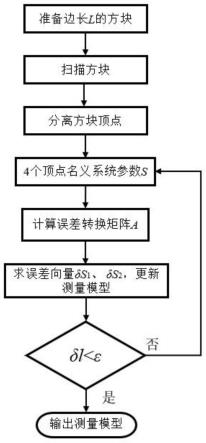
14.图1为三维激光扫描系统校准的流程图；
15.图2为三维激光扫描系统测量参数说明图；
16.图3为方块各顶点扫描测量图。
具体实施方式
17.为了使本发明的目的、技术方案及优点更加清晰，下面结合附图和具体实施方式对本发明进行详细说明。
18.三维激光扫描系统的自校准方法流程参见图1，具体步骤如下：
19.步骤1：确定激光扫描系统的测量模型，根据扫描系统采样点密度、扫描范围，准备一块边长为l的正方体方块；
20.本发明研究的三维激光扫描系统，是通过将现有线激光安装于旋转云台上实现对空间环境的三维扫描测算，参见图2，线激光返回扫描扇形区域内各测量点与扫描中心的距离r，扇形区域内的转角α；线激光安装于回转平台上，绕水平轴旋转，回转平台转角β可实时读取；回转轴与底座距离d，扫描扇面保持平行，与回转轴线距离为a；本扫描系统的测量参数s＝[a，d，r，α，β]
t
与测点p坐标的关系如下：
[0021][0022]
其中：x，y，z表示各测量点在扫描系统坐标系o-xyz下的坐标，坐标系原点定在回转平台底面中心，α，r通过线激光返回数据提取，β由回转平台编码器实时返回；a，d为固定值，可通过云台及线激光设计图纸获得其设计值。
[0023]
确定扫描系统的测量模型后，需准备一尺寸已知的正方体方块作为标定物，边长l不宜太大或太小，尺寸若接近或者小于扫描系统采样点间距，则无法完整获取方块的各个顶点；尺寸若远大于扫描中心与底座距离d，则会出现无法扫描到方块上表面，影响顶点坐
标的获取精度。此外，方块不能是玻璃、塑料等反射效果强烈的材质，避免扫描探头无法捕捉反射回来的激光。本发明所研究的三维扫描系统测量点间隔0.5
°
，扫描范围可达10m，方块采用铝合金材质，表面喷着色剂，边长为10cm。
[0024]
步骤2：将方块置于扫描系统的扫描范围内进行扫测，分离出方块4个顶点坐标及对应的测量参数。
[0025]
将方块置于扫描系统的扫描范围内，方块与扫描系统平台底座处于同一平面；方块与扫描设备的距离不宜太近或太远，太近时扫描区域仅能覆盖方块某一个面，太远时采样点太稀疏，很难获得准确的顶点坐标；同时需避免方块某个面正对扫描探头的情况，应当以方块的某条边对准扫描探头，使扫描区域能完整覆盖到方块上表面及两个侧面，参考图3，在扫描到的点云数据中，分离4个方块顶点，则点p3的实际z坐标为0，点p0、p1、p2的实际z坐标为l。在本发明研究中，方块离扫描探头距离在0.9m左右，测量点间距在2.6mm～3.5mm内。
[0026]
由于测量点之间存在间距，很难覆盖方块各个顶点，但必然会有些采样点落在方块的边线上面或者无限接近于边线，故而可以首先通过点云法矢分类提取出方块边线上及其附近的点云，通过ransac(随机采样一致)方法对边线点云进行处理，拟合出方块边线，求出相邻边线的交点即为方块顶点，假设得到的4个相邻顶点的坐标p0＝[x0,y0,z0]
t
，p1＝[x1,y1,z1]
t
，p2＝[x2,y2,z2]
t
，p3＝[x3,y3,z3]
t
。
[0027]
步骤3：建立扫描校准模型，计算4个顶点对应的误差转换矩阵；
[0028]
p0与相邻顶点之间的测量距离：
[0029][0030]
对上式两边微分有：
[0031][0032]
式(3)可简记为：
[0033]
δli＝(p
i-p0)
t
(a
i-a0)δs/liꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0034]
式中a表示误差转换矩阵：
[0035][0036]
通过计算观察发现误差转换矩阵a求差运算之后，a
i-a0第2列元素全为0，说明δl与d的偏差值δd无关；(p
i-p0)
t
(a
i-a0)第5列元素全为0，说明δl与β的偏差值δβ无关；故而可将上式中d，β的相关项剔除，先对a，r，α三个变量进行校准；记s1＝[a，r，α]
t
，s2＝[d，β]
t
，矩阵a更新为：
[0037][0038]
则有：
[0039]
(l
i-l)li＝(p
i-p0)
t
(a
i-a0)δs1ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0040]
步骤4：通过最小二乘法优化求解出各测量参数修正量，对测量模型进行修正：
[0041]
每次测量方块4个顶点，可以获得3组l与对应的δl，可将式(7)扩展为如下线性方程：
[0042][0043]
简记为：
[0044][0045]
式中：
[0046][0047]
可求出测量参数s1的误差：
[0048][0049]
对点p0、p1、p2的z坐标进行微分可得：
[0050][0051]
其中：
[0052][0053]
通过最小二乘法可求出测量参数s2的误差：
[0054][0055]
式中，(k
2t
k2)-1k2t
为k2的伪逆。
[0056]
根据式(14)、(19)计算出测量参数误差δs1、δs2后，则可对测量模型进行修正：
[0057][0058]
步骤5：重复步骤3、步骤4，直到距离测算误差在容许值内；
[0059]
根据式(15)更新后的测量模型，可从新获得方块4个相邻顶点的坐标p0，p1，p2，p3，重复步骤3、步骤4，可获得一组新的s1、s2及测量模型，直到距离测算误差δl在容许值ε内，输出更新后的测量模型。