一种太赫兹SAR二维自聚焦成像算法

本发明涉及雷达信号处理，尤其涉及一种太赫兹sar二维自聚焦成像算法。

背景技术：

1、太赫兹(terahertz,thz)波是指频谱在100ghz至10thz之间的电磁波，具有载频高、通信容量大、穿透性好、光子能量低、无生物电离等特点。与微波合成孔径雷达(synthetic aperture radar，sar)成像相比，太赫兹合成孔径雷达(thz-sar)成像具有更高分辨率、更高帧率、更高检测概率和更容易识别等显著优势，使其在现代雷达成像领域中受到越来越多的关注。

2、thz-sar成像时通常会受到一些非理想因素的影响，在雷达回波信号中引入相位误差。该误差可分为距离向和方位向两部分。其中距离向相位误差是由于基于固态源的太赫兹雷达系统只能通过多次倍频产生太赫兹信号，而扫频源和收发链路倍频器的非理想特性使得在太赫兹信号中引入非线性相位误差。这些非线性相位误差将直接影响目标回波的相位，从而导致距离像畸变和分辨率下降，造成目标支撑区不符合真实情况。而方位向相位误差是由于载机平台受到气流等因素影响使得飞行轨迹偏离理想状态而引入的平台运动误差导致的。现代sar系统中,通过惯性测量单元(inertial measurement unit，imu)和全球定位系统(global positioning system,gps)的结合可测量出平台的运动状态数据，然后通过测量数据对回波进行补偿。而对thz-sar来说，其波长较短使得较小的振动误差对回波相位的影响都不能忽略，这使得现有传感器达不到补偿所需要的精度要求。因此，对于上述的距离向和方位向相位误差，在进行基于测量数据的补偿后还需要利用自聚焦算法来提高成像质量。

3、子孔径相关(map drift,md)和相位梯度自聚焦(phase gradient autofocus,pga)是比较重要的两种自聚焦算法。md方法的缺点是只能估计二次相位误差，改进的多子孔径相关算法原理上能估计高阶相位误差，但由于子孔径过短而使估计结果偏差更大，往往不能适应高分辨成像的要求。pga的鲁棒性好且成像效率高，但必须在有特显点的情况下才能有效补偿误差，在实际应用中具有局限性。最小熵(minimum entropy algorithm，mea)算法基于整体图像熵值无需特显点，应用范围更广，更具有实用性。

技术实现思路

1、本发明的目的是为了提供一种太赫兹sar二维自聚焦成像算法，通过基于测量数据补偿和基于mea的二维自聚焦算法的联合，获得thz-sar高分辨聚焦图像。

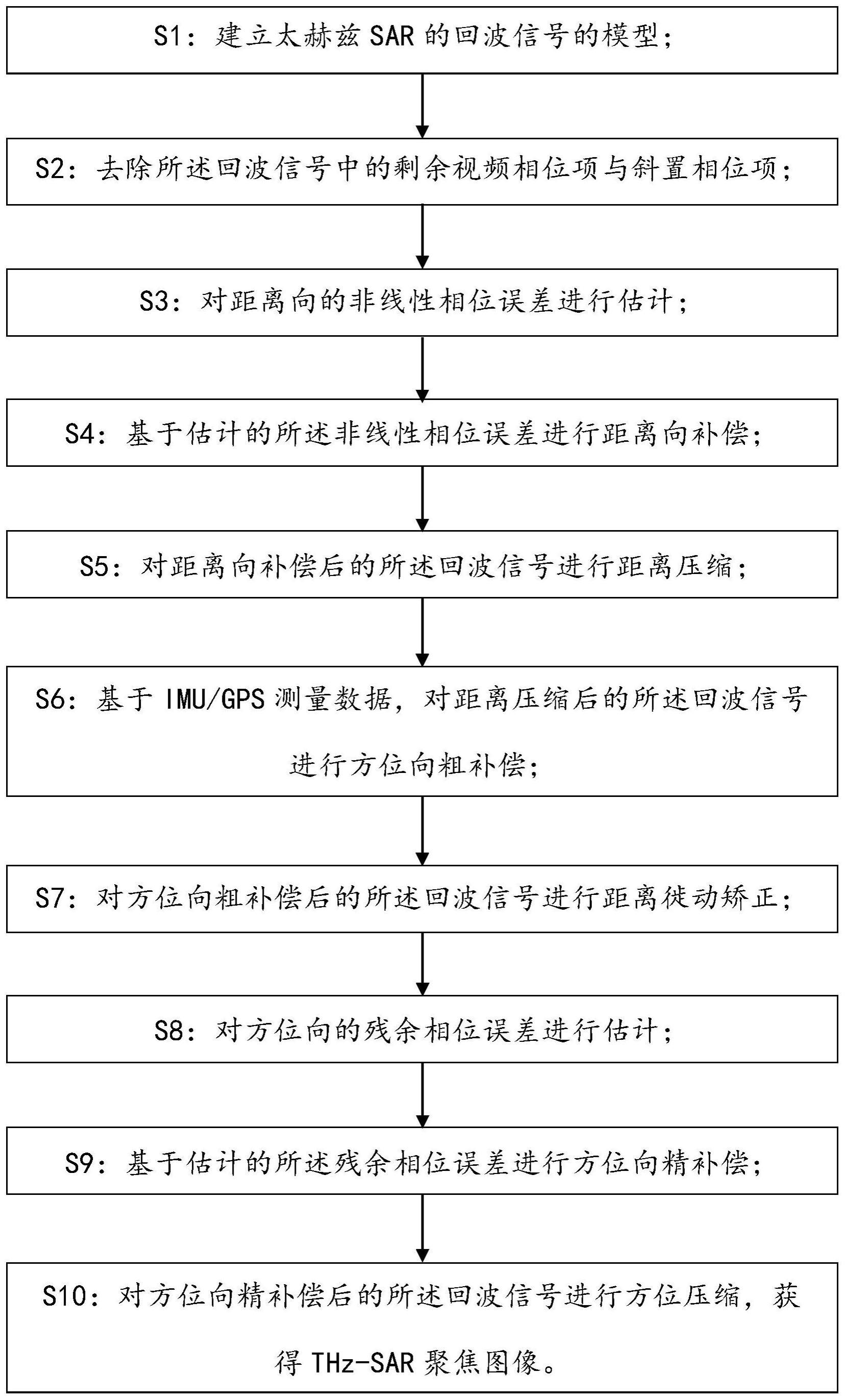
2、为了实现上述目的，本发明提出一种太赫兹sar二维自聚焦成像算法，包括以下步骤：

3、s1：建立太赫兹sar的回波信号的模型；

4、s2：去除所述回波信号中的剩余视频相位项与斜置相位项；

5、s3：对距离向的非线性相位误差进行估计；

6、s4：基于估计的所述非线性相位误差进行距离向补偿；

7、s5：对距离向补偿后的所述回波信号进行距离压缩；

8、s6：基于imu/gps测量数据，对距离压缩后的所述回波信号进行方位向粗补偿；

9、s7：对方位向粗补偿后的所述回波信号进行距离徙动矫正；

10、s8：对方位向的残余相位误差进行估计；

11、s9：基于估计的所述残余相位误差进行方位向精补偿；

12、s10：对方位向精补偿后的所述回波信号进行方位压缩，获得thz-sar聚焦图像。

13、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s1中，所述太赫兹sar发射线性调频脉冲信号，并将接收的回波信号进行解线性调频，生成的所述回波信号的模型表达式为：

14、

15、其中：τ为距离向快时间；t为方位向慢时间；tp为脉冲宽度；c为光速；λ为波长；ri为雷达的实际距离；rref为雷达的参考距离；rδ为雷达的实际距离与参考距离之差；j为虚数单位；γ为调频斜率。

16、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s2中，对式(1)进行距离向的傅里叶变换(fft)，可得：

17、

18、其中：fr为距离向频率；fc为中心频率；为多普勒项；为剩余视频相位项；为回波包络的斜置相位项；

19、式(2)中的剩余视频相位项和斜置相位项表示为：

20、

21、式(2)乘以所述剩余视频相位项与斜置相位项的补偿函数可得：

22、

23、对式(4)进行快时间的傅里叶逆变换(ifft)，即变换后所述回波信号的模型表达式为：

24、

25、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s3中，假设距离向的所述非线性相位误差的函数为则存在所述非线性相位误差的所述回波信号的模型表达式为：

26、

27、其中：τ为距离向快时间；t为方位向慢时间；

28、将τ和t分别离散化为tn(n＝0：n-1)和tm(m＝0：m-1)，则式(6)离散化，可得：

29、

30、将最小熵准则作为评价准则，通过迭代优化进行所述非线性相位误差的估计，具体步骤如下：

31、s3.1：假设估计的距离向的所述非线性相位误差为且初始化设置为0，即补偿后的距离像表达式为：

32、

33、其中：k为距离频率；m为回波脉冲数目；n为距离单元；n为总的距离单元数；

34、s3.2：基于最小熵准则，建立相位误差的模型，表达式为：

35、

36、其中：ent为图像熵值，表达式为：

37、

38、其中：e为距离像能量，表达式为：

39、

40、s3.3：基于牛顿法求解式(9)，可得所述相位误差进行迭代的表达式为：

41、

42、其中：

43、

44、

45、其中：s0(l-1)(n，m)为利用第(l-1)次迭代估计的相位误差进行校正后的所述回波数据；为gk，m中每个元素取复共轭；

46、s3.4：判断估计的所述相位误差是否足够精确，即判断第l次与第(l-1)次迭代后分别求出的所述图像熵值ent与ent(l-1)之间的差值是否低于预先设置的门限值j，即：

47、|ent(l)-ent(l-1)|≤j   (13)

48、若满足式(13)，则所需要补偿的距离向的所述非线性相位误差为：

49、

50、在步骤s4中，根据步骤s3估计的所述非线性相位误差则距离向的所述非线性相位误差的补偿函数为并乘以式(7)以对所述回波信号进行距离向补偿，可得：

51、

52、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s5中，对距离向补偿后的所述回波信号进行距离向傅里叶变换(fft)，完成距离压缩的所述回波信号的模型表达式为：

53、

54、其中：ti为目标到雷达的离散延迟快时间；为波束中心穿过目标的离散慢时间；b为距离向信号带宽；wa(·)为方位向包络；

55、基于运动相位误差的存在，实际上完成距离压缩的所述回波信号的模型表达式为：

56、

57、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s6中，基于imu/gps测量数据，计算获得天线和场景的实际斜距与理想斜距之间的差值dlos(tn，tm)，以进行相应的运动相位补偿，且所述运动相位误差的补偿函数为：

58、

59、式(17)乘以式(18)以对所述回波信号进行方位向粗补偿，可得：

60、sa，com1(tn，tm)＝sa(tn，tm)·dcom

61、

62、基于方位向因所述imu/gps测量数据存在的残余相位误差对式(19)进行变换，可得：

63、

64、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s7中，对方位向粗补偿后的所述回波信号进行方位向傅里叶变换(fft)，所述回波信号变换到距离多普勒域，通过插值对所述回波信号进行距离徙动矫正，在消除所述距离徙动的影响后，对所述回波信号进行方位向傅里叶逆变换(ifft)，可得：

65、

66、其中：为目标到雷达最近斜距的离散延迟快时间。

67、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s8中，基于最小熵准则，通过步骤s3.2中的所述相位误差的模型进行方位向的残余相位误差的估计，经过l次迭代后，判断求出的所述图像熵值ent是否满足式(13)，若满足，则所需要补偿的方位向的所述残余相位误差为：

68、

69、在步骤s9中，根据步骤s8估计的所述残余相位误差则方位向的所述残余相位误差的补偿函数为并乘以式(21)以对所述回波信号进行方位向精补偿，可得：

70、

71、进一步地，在所述的太赫兹sar二维自聚焦成像算法中，在步骤s10中，对精补偿后的所述回波信号进行匹配滤波，完成方位压缩后，获得的thz-sar聚焦图像的模型表达式为：

72、

73、其中：bd为多普勒带宽。

74、与现有技术相比，本发明的有益效果主要体现在：综合考虑了距离向的非线性相位误差和方位向的运动相位误差，并估计后相应的进行补偿，以获得高分辨的thz-sar聚焦图像；同时，基于imu/gps测量数据和mea自聚焦算法的联合使用，相较于直接采用自聚焦算法能有效降低了运算量。