基于最小二乘迭代计算的开关损耗拟合方法与流程

1.本发明属于汽车电驱动系统结温估算模型中开关损耗拟合计算技术领域，具体涉及一种基于最小二乘迭代计算的开关损耗拟合方法。


背景技术：

2.在现有汽车电驱动系统结温估算模型中，其开关损耗模型的参数是由双脉冲测试的数据拟合得到。拟合的损耗ex是关于温度tj、母线电压v
dc
以及电流i的函数。常规的拟合方法是通过类似求偏导的方法，对每个变量的系数进行分步拟合。这种方法对所提供的原始数据一致性要求较高，例如，在某个温度、电压，不同电流下的测试数据，必须保证测试所有数据中的电压值离目标电压值较近；且当拟合精度不理想时，还需要人工手动调整参数并校验，这会花费较多的时间。
3.因此，针对上述问题，予以进一步改进。


技术实现要素：

4.本发明的主要目的在于提供基于最小二乘迭代计算的开关损耗拟合方法，对原始测试数据一致性要求低，且由于迭代后会收敛至最小二乘解，其拟合精度高，可达数值最优解，具有拟合精度高、通用性强和对原始测试数据一致性要求低等优点，并且可通过编程实现自校验拟合，无需人工手动校验，从而节省开发时间。
5.为达到以上目的，本发明提供一种基于最小二乘迭代计算的开关损耗拟合方法，对结温估算模型的开关损耗模型的数据进行处理，包括以下步骤：
6.步骤s1：在结温估算模型中，设定开关损耗模型的拟合公式为：
[0007][0008]
其中，a0、a1、b1、a2、b2、a3、b3、c3为8个待求系数；v
dc
为母线电压；tj为结温；i为电流；ex为损耗(可为开通损耗eon、关断损耗eoff或反向恢复损耗erec)；
[0009]
步骤s2：计算5个待求系数a0、a1、b1、a2、b2，获取一组双脉冲测试数据exk(t
jk
,v
dck
,ik)，k＝1,2,...,n
，
n＞8，并且给定初始值a3、b3、c3，将双脉冲测试数据和初始值a3、b3、c3带入步骤s1的拟合公式，以获得一组线性方程并且矩阵形式为：
[0010]
ax1＝b；
[0011]
其中，系数矩阵an×5第k行的元素为：
[0012][0013]
解向量x1和已知向量b分别为：
[0014]
x1＝[a
0 a
1 b
1 a
2 b2]
t
；
[0015]
b＝[ex
1 ex2...exk...exn]
t
；
[0016]
由于步骤s2中的矩阵形式是超定的，进而用最小二乘法求解得到a0、a1、b1、a2、b2，并且对给定的初始值a3、b3、c3进行修正(由于一开始给定的a3、b3、c3初始值并不准确，因此
需要修正)；
[0017]
步骤s3：计算3个待求系数a3、b3、c3，将同一组双脉冲测试数据及求解得到的a0、a1、b1、a2、b2带入步骤s1的拟合公式，以获得一组线性方程，其矩阵形式为：
[0018]
cx2＝b；
[0019]
其中，系数矩阵cn×3第k行的元素为：
[0020][0021]
解向量x2为：
[0022]
x2＝[a
3 b
3 c3]
t
；
[0023]
由于步骤s3中的矩阵形式是超定的，进而用最小二乘法求解得到a3、b3、c3，并且将计算得到的a3、b3、c3替代步骤s2的矩阵形式中的a3、b3、c3的初始值，重复迭代过程预设次数直至收敛，最终获得满足精度要求的待求系数a0、a1、b1、a2、b2、a3、b3、c3。
[0024]
作为上述技术方案的进一步优选的技术方案，在步骤s3中，重复迭代过程为在(上一次步骤s3)新计算得到的a3、b3、c3替代步骤s2的矩阵形式中的a3、b3、c3的初始值并且进行计算，然后再将新得到的a0、a1、b1、a2、b2在步骤s3进行计算，以获得再次新的a3、b3、c3的初始值，通过步骤s2和步骤s3的不断重复迭代计算，进而在收敛状态下最终获得满足精度要求的待求系数a0、a1、b1、a2、b2、a3、b3、c3。
[0025]
作为上述技术方案的进一步优选的技术方案，在步骤s2中，第一次给定初始值a3、b3、c3时，满足a3、b3、c3均不为0，取a3＝1、b3＝1、c3＝1。
[0026]
为达到以上目的，本发明还提供一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现所述基于最小二乘迭代计算的开关损耗拟合方法的步骤。
[0027]
为达到以上目的，本发明还提供一种非暂态计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现所述基于最小二乘迭代计算的开关损耗拟合方法的步骤。
[0028]
本发明的有益效果为：
[0029]
本发明采用了最小二乘迭代计算的方法来拟合开关损耗。常规的分步拟合方法的对原始数据一致性要求较高，且在拟合精度不理想时，需要人工手动调整参数并校验。而本发明所提出的最小二乘迭代计算的方法对原始测试数据一致性要求低，且由于迭代后会收敛至最小二乘解，其拟合精度高，可达数值最优解。
附图说明
[0030]
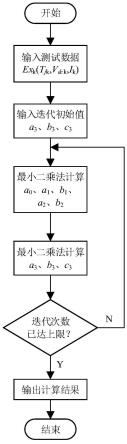
图1是本发明的基于最小二乘迭代计算的开关损耗拟合方法的示意图。
具体实施方式
[0031]
以下描述用于揭露本发明以使本领域技术人员能够实现本发明。以下描述中的优选实施例只作为举例，本领域技术人员可以想到其他显而易见的变型。在以下描述中界定的本发明的基本原理可以应用于其他实施方案、变形方案、改进方案、等同方案以及没有背离本发明的精神和范围的其他技术方案。
[0032]
在本发明的优选实施例中，本领域技术人员应注意，本发明所涉及的汽车电驱动系统、结温估算模型和开关损耗模型等可被视为现有技术。
[0033]
优选实施例。
[0034]
本发明公开了一种基于最小二乘迭代计算的开关损耗拟合方法，对结温估算模型的开关损耗模型的数据进行处理，包括以下步骤：
[0035]
步骤s1：在结温估算模型中，设定开关损耗模型的拟合公式为：
[0036][0037]
其中，a0、a1、b1、a2、b2、a3、b3、c3为8个待求系数；v
dc
为母线电压；tj为结温；i为电流；ex为损耗(可为开通损耗eon、关断损耗eoff或反向恢复损耗erec)；
[0038]
步骤s2：计算5个待求系数a0、a1、b1、a2、b2，获取一组双脉冲测试数据exk(t
jk
,v
dck
,ik)，k＝1,2,...,n，n＞8，并且给定初始值a3、b3、c3，将双脉冲测试数据和初始值a3、b3、c3带入步骤s1的拟合公式，以获得一组线性方程并且矩阵形式为：
[0039]
ax1＝b；
[0040]
其中，系数矩阵an×5第k行的元素为：
[0041][0042]
解向量x1和已知向量b分别为：
[0043]
x1＝[a
0 a
1 b
1 a
2 b2]
t
；
[0044]
b＝[ex
1 ex2...exk...exn]
t
；
[0045]
由于步骤s2中的矩阵形式是超定的，进而用最小二乘法求解得到a0、a1、b1、a2、b2，并且对给定的初始值a3、b3、c3进行修正(由于一开始给定的a3、b3、c3初始值并不准确，因此需要修正)；
[0046]
步骤s3：计算3个待求系数a3、b3、c3，将同一组双脉冲测试数据及求解得到的a0、a1、b1、a2、b2带入步骤s1的拟合公式，以获得一组线性方程，其矩阵形式为：
[0047]
cx2＝b；
[0048]
其中，系数矩阵cn×3第k行的元素为：
[0049][0050]
解向量x2为：
[0051]
x2＝[a
3 b
3 c3]
t
；
[0052]
由于步骤s3中的矩阵形式是超定的，进而用最小二乘法求解得到a3、b3、c3，并且将计算得到的a3、b3、c3替代步骤s2的矩阵形式中的a3、b3、c3的初始值，重复迭代过程预设次数直至收敛，最终获得满足精度要求的待求系数a0、a1、b1、a2、b2、a3、b3、c3。
[0053]
具体的是，在步骤s3中，重复迭代过程为在(上一次步骤s3)新计算得到的a3、b3、c3替代步骤s2的矩阵形式中的a3、b3、c3的初始值并且进行计算，然后再将新得到的a0、a1、b1、a2、b2在步骤s3进行计算，以获得再次新的a3、b3、c3的初始值，通过步骤s2和步骤s3的不断重复迭代计算，进而在收敛状态下最终获得满足精度要求的待求系数a0、a1、b1、a2、b2、a3、b3、c3。
[0054]
更具体的是，在步骤s2中，第一次给定初始值a3、b3、c3时，满足a3、b3、c3均不为0，取a3＝1、b3＝1、c3＝1。
[0055]
本发明还公开了一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现所述基于最小二乘迭代计算的开关损耗拟合方法的步骤。
[0056]
本发明还公开了一种非暂态计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现所述基于最小二乘迭代计算的开关损耗拟合方法的步骤。
[0057]
值得一提的是，本发明专利申请涉及的汽车电驱动系统、结温估算模型和开关损耗模型等技术特征应被视为现有技术，这些技术特征的具体结构、工作原理以及可能涉及到的控制方式、空间布置方式采用本领域的常规选择即可，不应被视为本发明专利的发明点所在，本发明专利不做进一步具体展开详述。
[0058]
对于本领域的技术人员而言，依然可以对前述各实施例所记载的技术方案进行修改，或对其中部分技术特征进行等同替换，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围。