一种基于非圆信号的新型移位阵列设计方法

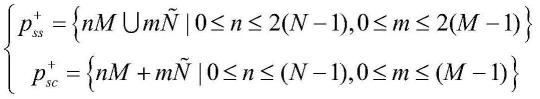
1.本发明涉及目标检测和信号处理领域，具体涉及一种用于非圆信号doa(direction of arrival)估计的新型移位阵列设计方法。


背景技术：

2.新技术革命浪潮下，高超声速目标、声呐雷达信号检测、复杂电子对抗等现代化技术手段的快速发展给现有空间和安全防控领域带来严峻考验。因此，利用新型阵列设计理论开展多目标doa估计算法研究，实现对敌方目标的快速有效定位，对于空间和安全防控领域具有重要的现实意义。
3.相比于均匀线阵，稀疏阵列具有更大的虚拟延迟、更高的自由度和更弱的互耦效应，带来了估计性能的极大提升，从而成为近年来doa估计问题的研究热点。在所有的稀疏阵列设计中，嵌套阵列和互质阵列是最具代表性的阵列设计方法，已有方法大多是基于上述方法的改进。嵌套阵列由单位间距的均匀子阵和较大间距的稀疏子阵排列构成，可以使用n个传感器估计o(n2)个信源，但嵌套阵列中的均匀子阵存在耦合效应，从而影响其估计性能。


技术实现要素：

4.本发明解决的技术问题是：针对现有模型doa估计问题，提出一种无孔虚拟阵列设计方法，实现高效的doa估计。
5.本发明的技术解决方案是：一种非圆信号新型移位阵列设计方法，步骤如下：
6.步骤1：对原始嵌套阵列的两组子阵列进行重新排列设计，以构建新型移位阵列；
7.步骤2：基于非圆信号椭圆协方差不为0的特性，计算新型移位阵列的差分共阵和求和共阵及其连续自由度；
8.步骤3：对目标信号源进行空间采样，计算新型移位阵列接收信号的协方差矩阵并将其向量化处理；
9.步骤4：构造选择矩阵，提取向量化矩阵中的非零元素；
10.步骤5：利用music算法实现目标信号源的doa估计。
11.进一步地，步骤1所述的新型移位阵列由两部分构成，在一条直线上排列的非均匀互质阵列，分别分为子阵一和子阵二。子阵一包含n个阵元，阵元间距为md；子阵二包含m-1个阵元，阵元间距为d；其中m＝4,d代表半波长。新型阵列的构型表达式为p＝p1∩p2,
[0012][0013]
其中,p1和p2分别代表子阵1和子阵2的物理阵元排列位置。
[0014]
进一步地，由于虚拟阵元的位置关于0位置对称，为了便于说明，仅取虚拟阵元的非负部分进行分析。步骤2中非圆信号的稀疏阵列总延迟由差分共阵与求和共阵p
s+
组
成，而差分共阵包括自差集和互差集而求和共阵p
s+
包括自和集与互和集相应的集合可表示为：
[0015][0016][0017][0018]
进一步地，步骤3中的接收信号表示为：其中，x(t)为接收信号矢量，sk(t)为发送信源，为相应于θk的导向矢量，dm代表第m个阵元与参考阵元之间的距离，a是阵列流形，为相位偏移矩阵,φk是第k个信源的非圆相位，s(t)为信源矢量，n(t)是功率为的加性高斯白噪声，n(t)为相应的噪声矩阵；
[0019]
非圆信号的协方差矩阵可表示为：
[0020][0021]
矢量化后的协方差矩阵为：
[0022][0023]
进一步地，步骤4中采用选择矩阵提取矢量化矩阵中的非零元素：
[0024]
zc＝j
·
z，
[0025]
其中j代表选择矩阵。
[0026]
本发明的有益效果：针对现有设计方法存在孔洞，连续滞后少的问题，通过改变阵元排布方式，基于非圆信号椭圆协方差不为0的特性，设计一种虚拟阵元无孔的移位阵列。给出了联合利用差分共阵与求和共阵条件下连续延迟的数学表达式，大大提高了自由度，增加了doa估计精度。
附图说明
[0027]
为使得本发明中的技术方案，下面将会选取一些附图对本发明进行阐述。下述附图仅为本发明的一些实例；使用者可根据该附图获得其他类似的附图。其中：
[0028]
图1为本发明的流程示意图；
[0029]
图2为同条件下本发明与原始互质阵列、原始嵌套阵列的空间谱图；
[0030]
图3为同条件下本发明与原始互质阵列、原始嵌套阵列的均方根误差随信噪比变化图；
[0031]
图4为同条件下本发明与原始互质阵列、原始嵌套阵列的均方根误差随快拍变化图；
具体实施方式
[0032]
下面将更加深刻，完整的阐述本发明实施案例中的技术方案。所述实施案例为部分实施案例。使用者可根据本发明，不需付出创造性劳动的获得其他实施案例。该“其他实施案例”均属于本发明保护的范围。
[0033]
如图1所示，一种无孔阵列doa估计流程图，包括以下步骤：
[0034]
对原始互质阵列进行重新排列设计构建新型移位阵列，新阵列包括子阵一和子阵二。子阵一包含n个阵元，阵元间距为md；子阵二包含m-1个阵元，阵元间距为d；其中m＝4,d代表半波长。新型阵列的构型表达式为p＝p1∩p2,
[0035][0036]
步骤2：计算新模型的差分共阵、求和共阵、以及连续自由度，包括：
[0037]
步骤2.1：计算差分共阵与求和共阵：非圆信号的稀疏阵列总延迟由差分共阵与求和共阵p
s+
组成，而差分共阵包括自差集和互差集而求和共阵p
s+
包括自和集与互和集由于虚拟阵元的位置关于0位置对称，为了便于说明，仅取虚拟阵元的非负部分进行分析。相应的集合可表示为：
[0038][0039][0040][0041]
步骤2.2：计算连续自由度：
[0042]
对于阵元数为q＝m+n-1的新型互质阵列，其连续自由度为：4(n-1)m+1。
[0043]
步骤3：对目标信号源进行采样，并对接收信号的协方差矩阵进行向量化处理，包括：
[0044]
步骤3.1：对目标信号源进行采样，得到接收信号向量表示为：
[0045][0046]
其中，x(t)为接收信号，sk(t)为发送信号，为相应于θk的导向矢量，dm代表第m个阵元与参考阵元之间的距离，a是阵列流形，为相位偏移矩阵,φk是第k个信源的非圆相位，s(t)为信源矢量，n(t)是功率为的加性高斯白噪声，n(t)为相应的噪声矩阵；
[0047]
步骤3.2：计算接收到的非圆信号的协方差矩阵，可表示为：
[0048][0049]
步骤3.3：对协方差矩阵矢量化处理：
[0050][0051]
步骤4：采用选择矩阵提取矢量化矩阵中的非零元素：
[0052]
zc＝j
·
z，
[0053]
其中j代表选择矩阵。
[0054]
步骤5：利用music算法实现目标信号源的doa估计。
[0055]
具体实施例
[0056]
现在结合附图2——4对本发明作进一步详细的说明。
[0057]
采用阵元数目q＝m+n-1＝12的物理阵列，其中m＝4,n＝9。子阵1包含n个间距为md的物理阵元，子阵2包含m个间距为d的物理阵元，物理阵元排列位置为{0,4,8,12,16,20,24,28,29,30,31,32}。利用非圆信号椭圆协方差不为0的特性，差分共阵与求和共阵的虚拟阵元范围为[-64,64]，虚拟阵列的连续自由度为129。
[0058]
仿真1：10个非圆入射信源均匀分布在[-40
°
，40
°
]，信噪比为-5db，快拍为500。由图2可以看出，本发明设计的模型由于提供更高的虚拟阵元，与其它两种模型的空间谱相比，图2.(c)中的谱峰更尖锐，对信号的估计效果更精准，可以更准确的估计入射信号的位置。
[0059]
仿真2：均方根误差随信噪比性能
[0060]
采用均方根误差对三种阵列进行估计性能评估：
[0061][0062]
上式中为第i次蒙特卡洛实验的第q个信号源的doa估计，θq是真实的信号源角度。仿真参数与实验1相同，除了蒙特卡洛为1000，快拍为2000，信噪比变化区间为[-5,20]，从图3可以看出，优化后的阵列优于互质阵列原始模型、嵌套阵列，因为本发明的阵列具有更长的阵列孔径、更多的连续虚拟阵元，所以获得了更好的估计性能。
[0063]
仿真3：均方根误差随快拍变化图
[0064]
仿真条件与实验2相同，除了信噪比设置为20,图4为快拍数由500增加到3000时的均方根误差图，可以看出，随着快照数的增加，所有阵列构型的均方根误差均逐渐减小并趋于稳定，而本发明的阵列的性能优于其他阵列。归其原因，主要是由于提出阵列孔径大、连续延迟多，带来了性能提升。
[0065]
以上所述仅为本发明的一个实施方式而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。