一种基于蠕变变形机制的高温蠕变寿命预测方法

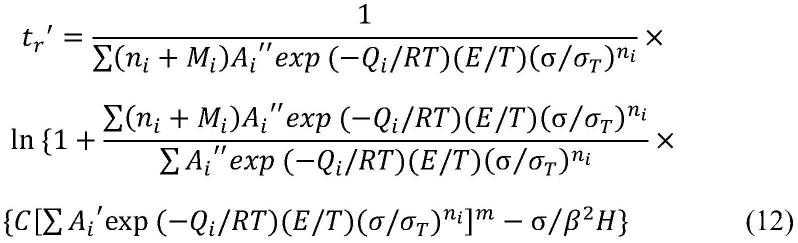
1.本发明涉及寿命预测领域，尤其是一种基于蠕变变形机制的高温蠕变寿命预测方法。


背景技术：

2.在核电、航空、化工等领域，设备通常在高温条件下服役，高温下材料会发生蠕变导致设备失效，因此，蠕变寿命是高温材料的重要性能之一，对材料进行蠕变寿命预测也不可或缺。目前广泛采用的larson-miller(lm)、orr-sherby-dorn(osd)参数法依据短时蠕变数据外推预测材料的蠕变寿命，无法预测不同蠕变机制主导时材料的蠕变寿命，而基于变形机制的真应力应变模型没有考虑晶粒尺寸的影响，材料寿命预测的精度不高，传统的延性耗竭法采用断裂应变作为蠕变延性建立蠕变延性与最小蠕变速率之间的关系，未考虑材料断裂前颈缩引起的塑性变形对断裂应变的影响。


技术实现要素：

3.针对上述现有技术的不足，本发明提供一种基于蠕变变形机制的蠕变寿命预测方法，使用90％寿命处的应变作为蠕变延性修正延性耗竭法，并考虑晶粒尺寸的影响，能够精准预测多种蠕变机制主导下材料的蠕变寿命。
4.为了实现上述目的，本发明提供一种考虑不同蠕变机制作用的高温蠕变寿命预测方法，包括以下步骤：
5.s1：在不同试验温度下，对材料进行不同应力水平的蠕变断裂试验；
6.s2：根据所述蠕变断裂实验的结果，建立所述材料的稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式；
7.s3：根据上述稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式，得到蠕变应变ε随蠕变时间t变化的函数关系；
8.s4：根据上述蠕变应变ε随蠕变时间t变化的函数关系，得到蠕变断裂时间tr的计算式；
9.s5：考虑尺寸效应，得到修正后上述蠕变断裂时间tr′
的计算式；
10.s6：采用90％断裂寿命处的应变作为蠕变延性的延性耗竭法，得到蠕变延性ε
0.9
与稳态/最小蠕变应变率的函数关系式；
11.s7：根据所述稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式，所述修正后的蠕变断裂时间tr′
的计算式，所述蠕变延性ε
0.9
与稳态/最小蠕变应变率的函数关系式，得到蠕变断裂时间tr′
与应力σ、温度t的函数关系式，预测所述材料的蠕变寿命。
12.进一步地，所述s2包括：
13.s21：采用诺顿幂律方程形式，不同蠕变变形机制下蠕变应变率与应力σ、温度t之间的函数关系表示为：
[0014][0015]
式(1)中，i＝s,g,c；s表示晶界滑移蠕变机制，g表示位错滑移蠕变机制，c表示位错攀移蠕变机制(本文下标i均表示此含义，不再赘述)；a表示材料常数，n表示应力指数；q表示蠕变激活能；r表示摩尔气体常数，r＝8.314j/(k
·
mol)。
[0016]
s22：采用bmd方程，改写式(1)，并采用抗拉强度σ
t
或弹性模量e规则化应力σ(为书写方便，只列了用抗拉强度σ
t
规则化应力的公式，但公式中σ
t
均可用e代替)，改写后蠕变应变率与应力σ、温度t之间的函数关系表示为：
[0017][0018]
式(2)中，a0表示材料常数；d0表示扩散系数；k表示boltzmann常数；e表示材料在试验温度下的弹性模量；b表示柏氏矢量。
[0019]
s23：各变形机制蠕变速率线性累加，得到稳态/最小蠕变速率为：
[0020][0021]
式(3)中，ai′
＝a
i0di0
(b/k)
[0022]
s24：引入真应力应变关系：
[0023]
σ＝σ0exp(ε)
ꢀꢀꢀ
(4-a)
[0024]
ε＝ln(1+e)
ꢀꢀꢀ
(4-b)
[0025]
式(4-a)、(4-b)中，σ0表示名义工程应力，e表示工程应变。
[0026]
s25：考虑位错攀移蠕变变形机制导致的位错增值效应：
[0027][0028]
式(5)中，当i＝s、g时，mi＝0；m表示位错增值系数。
[0029]
s26：根据式(4-a)、式(5)，并利用泰勒级数展开得到：
[0030][0031]
式(6)中，
[0032]
进一步地，所述s3包括：
[0033]
s31：对式(6)积分得到蠕变第二阶段蠕变应变ε
ss
：
[0034][0035]
s32：根据晶界滑移蠕变变形机制下瞬态蠕变计算公式，蠕变应变ε随蠕变时间t变化的函数关系表示为：
[0036][0037][0038]
式(8)中，ε
e0
表示初始弹塑性应变；表示第一阶段的蠕变应变，
β表示材料常数，h表示晶界滑移机制加工硬化系数；(当i＝s时)，表示第一阶段蠕变时间。
[0039]
进一步地，根据上述蠕变应变ε随蠕变时间t变化的函数关系，当蠕变时间t很大时，exp(-t/t
t
)趋于0，并可以忽略式(8)中初始弹塑性应变ε
e0
，所述s4中蠕变断裂时间tr的计算式为：
[0040][0041]
式(9)中，εr表示蠕变断裂应变。
[0042]
进一步地，所述s5中，考虑晶粒尺寸，修正后的断裂时间tr′
计算式为：
[0043][0044]
式(10)中，p为晶粒尺寸指数。
[0045]
进一步地，所述s6中用90％断裂寿命处的应变ε
0.9
作为蠕变失效应变εr，建立ε
0.9
与稳态/最小蠕变应变率的函数关系式：
[0046][0047]
进一步地，根据上述式(6)、(10)、(11)，所述s7中蠕变断裂时间tr
′
与应力σ、温度t的函数关系式为：
[0048][0049]
本发明一种基于蠕变变形机制的蠕变寿命预测方法有如下优点：
[0050]
1)运用90％断裂寿命处的应变作为断裂应变修正延性耗竭法模型，使该方法能够精确预测材料的蠕变寿命。并且适用于不同温度应力条件下，考虑不同蠕变机制主导时材料的蠕变寿命；
[0051]
2)考虑晶粒尺寸的影响，提高预测精度。
附图说明
[0052]
图1为本发明的蠕变寿命预测方法的流程图；
[0053]
图2为根据本发明的一个实施例求取应力指数的拟合结果图；
[0054]
图3为根据本发明的一个实施例求取蠕变激活能的拟合结果图；
[0055]
图4为根据本发明的一个实施例求取用90％断裂寿命处应变ε
0.9
作为蠕变断裂应变εr的延性耗竭法常数的拟合结果图；
[0056]
图5为本发明实例的预测寿命结果图。
具体实施方式
[0057]
下面结合附图，以具体实例对本发明作进一步详细说明使能更好地理解本发明的功能和特点。
[0058]
如图1所示，本发明一种蠕变寿命预测方法包括以下步骤：
[0059]
s1：在不同试验温度下，实例部分选取800℃、850℃两个温度点，对sa508
‑ⅲ
钢进行15-30mpa应力水平的蠕变断裂试验。
[0060]
s2：根据所述蠕变断裂实验的结果，利用双对数坐标拟合材料常数，建立所述材料的稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式。
[0061]
s3：根据上述稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式，得到蠕变应变ε随蠕变时间t变化的函数关系。
[0062]
s4：根据上述蠕变应变ε随蠕变时间t变化的函数关系，得到蠕变断裂时间tr的计算式。
[0063]
s5：考虑尺寸效应，对上述计算式进行修正。
[0064]
s6：采用90％断裂寿命处的应变作为蠕变延性的延性耗竭法，得到蠕变延性ε
0.9
与稳态/最小蠕变应变率的函数关系式。
[0065]
s7：根据所述稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式，所述蠕变应变ε随蠕变时间t变化的函数关系，所述蠕变断裂应变εr与稳态/最小蠕变应变率的函数关系式，得到蠕变断裂时间tr与应力σ、温度t的函数关系式，预测所述材料的蠕变寿命。
[0066]
下面分别对上述s2-s6进行详细的描述：
[0067]
s2建立稳态/最小蠕变应变率与应力σ、温度t之间的函数关系式包括：
[0068]
首先采用诺顿幂律方程形式，不同蠕变变形机制下蠕变应变率与应力σ、温度t之间的函数关系表示为：
[0069][0070]
式(1)中，i＝s,g,c；s表示晶界滑移蠕变机制，g表示位错滑移蠕变机制，c表示位错攀移蠕变机制(后文下标i均表示此含义，不再赘述)；a表示材料常数，n表示应力指数；q表示蠕变激活能；r表示摩尔气体常数，r＝8.314j/(k
·
mol)。利用蠕变速率与应力双对数坐标曲线如图2所示拟合得到应力指数n。
[0071]
实例中对sa508
‑ⅲ
钢进行s1所述的蠕变断裂试验，并结合文献中900℃，1000℃下sa508
‑ⅲ
钢的蠕变试验数据，拟合出800℃、850℃、900℃、1000℃下的应力指数分别为3.56、3.36、3.22、3.40。根据不同蠕变机制对应的参数表，可以得出800-1000℃上述材料为单一位错滑移机制控制，取ng＝3。
[0072]
接着采用bmd方程，改写式(1)，并规则化应力，并采用抗拉强度σ
t
或弹性模量e规则化应力σ，改写后蠕变应变率与应力σ、温度t之间的函数关系表示为：
[0073][0074]
式(2)中，a0表示材料常数；d0表示扩散系数；k表示boltzmann常数；e表示材料在试验温度下的弹性模量；b表示柏氏矢量。实例中采用弹性模量e规则化应力σ，改写后蠕变应变率与应力σ、温度t之间的函数关系表示为：
[0075]
接着各变形机制蠕变速率线性累加，实例中温度与应力下，主导蠕变机制为位错滑移，得到稳态/最小蠕变速率为：
[0076][0077]
式(3)中，ai′
＝a
i0di0
(b/k)
[0078]
在实例中，式中ag′
＝a
g0dg0
(b/k)。
[0079]
然后考虑蠕变试验过程中试样形状的改变引起应力应变的改变，引入真应力应变关系：
[0080]
σ＝σ0exp(ε)
ꢀꢀꢀ
(4-a)
[0081]
ε＝ln(1+e)
ꢀꢀꢀ
(4-b)
[0082]
式(4-a)、(4-b)中，σ0表示名义工程应力，e表示工程应变。
[0083]
然后又考虑位错攀移蠕变变形机制导致的位错增值效应：
[0084][0085]
式(5)中，当i＝s、g时，mi＝0；m表示位错增值系数。在实例中，i＝g，故
[0086]
最后根据将式(4-a)代入式(5)，并利用泰勒级数将指数项展开，取展开式的前两项得到：
[0087][0088]
式(6)中，
[0089]
本实例中本实例中式中，
[0090]
s3建立蠕变应变ε随蠕变时间t变化的函数关系包括：
[0091]
首先对式(6)积分得到蠕变第二阶段蠕变应变ε
ss
：
[0092][0093]
实例中
[0094]
接着根据晶界滑移蠕变变形机制下瞬态蠕变计算公式，蠕变应变ε随蠕变时间t变化的函数关系表示为：
[0095][0096]
式(8)中，ε
e0
表示初始弹塑性应变；表示第一阶段的蠕变应变，β表示材料常数，h表示晶界滑移机制加工硬化系数；(当i＝s时)，表示第一阶段蠕变时间。本实例条件中，材料为单一位错滑移机制控制，故
[0097]
s4中，因为材料的蠕变试验时间很长，exp(-t/t
t
)趋于0，并可以忽略式(8)中初始弹塑性应变ε
e0
，简化式(8)得到蠕变断裂时间tr的计算式为：
[0098][0099]
式(9)中，εr表示蠕变断裂应变。
[0100]
实例中
[0101]
s5中，考虑尺寸效应：
[0102][0103]
式(10)中，p为晶粒尺寸指数。本实例中
[0104]
s6中用90％断裂寿命处的应变ε
0.9
作为蠕变断裂应变εr，建立ε
0.9
与稳态/最小蠕变应变率的函数关系式：
[0105][0106]
s7中，根据式(6)、(10)、(11)，蠕变断裂时间tr′
与应力σ、温度t的函数关系式为：
[0107][0108]
本实例中，
[0109][0110]
采用本发明的蠕变寿命预测方法对800℃、900℃的sa508
‑ⅲ
钢进行蠕变寿命预测。首先根据s1所述的蠕变断裂试验，并结合文献中900℃，1000℃下sa508
‑ⅲ
钢的蠕变试验数据，拟合出800℃、850℃、900℃、1000℃下的应力指数，如图2所示，分别为3.56、3.36、3.22、3.40。根据不同蠕变机制对应的参数表，可以得出800-1000℃上述材料为单一位错滑移机制控制，则应力指数ng＝3，晶粒尺寸指数pg＝0，然后根据800℃、850℃、900℃、1000℃下的试验数据拟合可得，在800-1000℃温度区间，蠕变激活能由图3拟合得出，qg＝61638j/mol，ag′
＝ag″
＝24292。根据800℃、850℃蠕变曲线在用90％断裂寿命处应变ε
0.9
作为蠕变断裂应变εr的延性耗竭法中，根据800℃、850℃下的蠕变断裂试验数据，材料常数由图4拟合求取，本实例中求得c＝44，m＝0.14。对sa508
‑ⅲ
钢在800℃下，应力为14mpa、26mpa和900℃下，应力为18mpa、22mpa、30mpa时的蠕变寿命进行预测，预测结果与试验结果比较，如图5所示。
[0111]
从图5可以看出，预测寿命精度在2.5倍误差带内，试验结果与预测结果接近，且预测结果具有保守性。由此可见，本发明所示的蠕变寿命预测模型可以预测800℃、900℃下不同应力水平sa508
‑ⅲ
钢的蠕变寿命。