一种基于形状-空间联合特征的曲面轮廓监控方法

1.本发明属于曲面监控技术领域，具体涉及一种基于形状-空间联合特征的曲面轮廓监控方法。


背景技术：

2.随着高精密光学测量和传感技术的应用和发展，对于曲面的测量已从传统的单点、片段测量迈向高稠密点云、全轮廓测量，如近年来应用广泛的激光三角测量仪、高精度复合式三维激光扫描仪等，它可以在几十秒内生成数十万点云数据以表征整个工件的三维曲面轮廓。
3.曲面轮廓质量是衡量工件加工质量的重要指标，它可以反映出工件在加工过程中受设备精度、原材料的成分以及加工工艺等各种因素的影响情况，故监控曲面轮廓质量的变化能更精确地识别工件加工质量特征是否在受控范围内。目前曲面轮廓监控方法主要有使用张量回归的多元线性代数方法建模和监测点云数据的结构，以及将三维点云转化为二维图像后监控等，这些方法只监控单一变量，仅仅提取了曲面点云离散的关键质量特性，未充分利用点云丰富的内在信息，无法检测出较小的质量缺陷或故障。同时，曲面点云的各点之间存在很强的空间相关性，而现有方法无法体现这种空间关系，所以在监控过程中常常会出现错检或漏检，对工件的生产制造过程产生了极大的影响。
4.目前常用的曲面轮廓监控方法基于参数化建模实现，通过将点云数据映射嵌入到它们的二维流形空间中，输入矢量来获得低维流形参数化，并对参数化模型进行监控。与传统方法相比，这种方法能够描述工件形状的变化，但它在监控前需要对曲面点云进行配准，计算成本较高，且其参数化模型仅仅考虑了工件形状的变化，未考虑工件表面点云的空间相关性，无法准确监控工件加工质量的变化。因此需要一种能够结合工件表面点云的空间相关性判断曲面轮廓是否合格的检测方法。


技术实现要素：

5.基于现有技术中存在的上述缺点和不足，本发明的目的之一是至少解决现有技术中存在的上述问题之一或多个，换言之，本发明的目的之一是提供满足前述需求之一或多个的一种基于形状-空间联合特征的曲面轮廓监控方法。
6.为了达到上述发明目的，本发明采用以下技术方案：
7.一种基于形状-空间联合特征的曲面轮廓监控方法，方法包括如下步骤：
8.s1、获取工件表面的点云数据；
9.s2、根据点云数据计算工件表面的拉普拉斯-贝尔特拉米谱，并选择拉普拉斯-贝尔特拉米谱的前若干个值的平均值作为工件表面的曲面特征数据；
10.s3、将点云数据以若干种不同的尺寸分割为分块点云；
11.s4、计算分块点云中任意两块点群的最小测地线距离，根据最小测地线距离构建空间测地线距离矩阵；
12.s5、根据空间测地线距离矩阵计算每个分块点云的greary’s g指数；
13.s6、选择greary’s g指数最低的分块点云的尺寸作为统计尺寸，根据统计尺寸计算每个分块点云的集聚度；
14.s7、根据集聚度及拉普拉斯-贝尔特拉米谱计算每个分块点云的hotelling’st2统计量；
15.s8、根据hotelling’s t2统计量检测存在异常曲面。
16.作为优选方案，步骤s1之后、s2之前还包括步骤：
17.s11、剔除点云数据中的离群点和冗余点。
18.作为优选方案，步骤s2具体包括如下步骤：
19.s21、根据每个点云数据生成对应的曲面模型；
20.s22、将曲面模型的曲面定义为黎曼流形；
21.s23、根据黎曼流形计算每个点云数据的拉普拉斯-贝尔特拉米谱；
22.s24、选择每个点云数据的拉普拉斯-贝尔特拉米谱中前若干个值的平均值作为点云数据对应工件表面的曲面特征数据。
23.作为进一步优选的方案，步骤s24中，选择每个点云数据的拉普拉斯-贝尔特拉米谱中前50个值的平均值作为工件表面的曲面特征数据。
24.作为优选方案，步骤s5之后、s6之前还包括步骤：
25.s51、根据空间测地线距离矩阵计算每个分块点云的z检验值，并删除z检验值低于预设值的点云分块尺寸。
26.作为优选方案，步骤s8具体包括：
27.s81、根据hotelling’s t2统计量生成hotelling’s t2控制图；
28.s82、根据hotelling’s t2控制图检测存在异常曲面。
29.7.如权利要求1的一种基于形状-空间联合特征的曲面轮廓监控方法，其特征在于，
30.步骤s3中，尺寸包括5
×
5mm、10
×
10mm、15
×
15mm、20
×
20mm、25
×
25mm、30
×
30mm、35
×
35mm、40
×
40mm、45
×
45mm、50
×
50mm。
31.本发明与现有技术相比，有益效果是：
32.本发明的方法利用了点云内在的丰富信息检测出工件表面的微小变化，实现了对工件表面质量变化的监控；
33.本发明的方法去除了传统曲面监控前配准的步骤，减少了点云预处理的时间，降低了曲面监控的成本。
附图说明
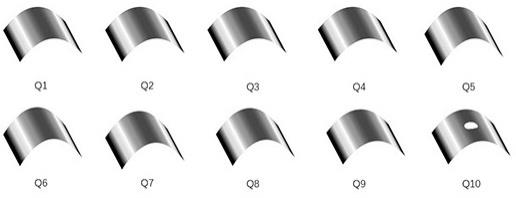
34.图1是本发明实施例的分块点云的示意图；
35.图2是本发明实施例的分块点云的greary’s g指数折线图；
36.图3是本发明实施例的分块点云的hotelling’s t2控制图。
具体实施方式
37.为了更清楚地说明本发明实施例，下面将对照附图说明本发明的具体实施方式。
显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图，并获得其他的实施方式。
38.实施例：本实施例提供一种基于形状-空间联合特征的曲面轮廓监控方法，具体包括如下步骤：
39.首先执行s1、获取工件表面的点云数据，点云数据可以采用激光扫描相机进行采集，在本实施例使用matlb人为生成十个曲面作为假想的工件表面，以供后续步骤根据该十个曲面示例本发明的具体实施方式。
40.生成的十片点云分别为q1、q2、q3、q4、q5、q6、q7、q8、q9、q10，曲面点云模型图如图1所示。其中q1-q8曲面的曲率有细微变化，但仍处于受控范围内；q9曲面相比于q1-q8曲面的曲率变化明显，处于失控状态；q10曲面的曲率虽然与q1-q8曲面的曲率相似，但具有20mm半径的孔洞，因此也处于失控状态。
41.进一步的，在步骤s1之后还包括步骤s11、剔除各个点云数据中的离群点和冗余点，提高曲面精度，筛除扫描误差。
42.s2、得到点云数据后，根据点云数据使用线性有限元方法计算其对应工件表面的拉普拉斯-贝尔特拉米谱。
43.点云数据不能直接用于曲面的线性有限元方法，本实施例提供步骤s2的一种实施方法，包括如下步骤：
44.s21、根据每个点云数据生成对应的曲面模型，使用工程建模软件如solidworks中的网格化功能将点云数据连接生成三角网格，然后进一步使用曲面生成功能将三角网格拟合为曲面模型；
45.s22、读取曲面模型文件，将曲面定义为黎曼流形m；
46.s23、根据黎曼流形计算每个点云数据的拉普拉斯-贝尔特拉米谱；
47.具体的，步骤s23的拉普拉斯-贝尔特拉米谱以如下方法计算：获取黎曼流形m上的亥姆霍兹方程
△mf＝λf，特征值的集合即为曲面的拉普拉斯-贝尔特拉米谱。
48.因此使用伽辽金变分公式将亥姆霍兹方程转换为：
49.,其中dv是流形上的表面元素。
50.因为其中g为流形表面度规张量，f为n个形状函数的线性组合：
[0051][0052]
最后得到
[0053]
将其写成矩阵形式的广义特征值问题：au＝λbu，其中和b
lm
＝《h
l
,hm》，对该a、b矩阵求解即可得到拉普拉斯-贝尔特拉米谱。
[0054]
a、b矩阵的求解过程如下：
[0055]
将曲面划分为若干个三角网格，先在局部坐标中参数化地描述由三个特殊坐标
(特殊坐标分别为p1(0,0,0)，p2(0,1,0)，p3(1,0,0))构成的特定三角形，此三角形中的点坐标为p(u,v,0)，其中0≤u≤1,0≤v≤1,u+v≤1。
[0056]
计算此平面的度量张量g，首先计算此三角形的两个顶点p2、p3在u、v两个方向上的偏导
[0057]
然后得到平面度量张量的分量
[0058]
由此计算得到平面的度量张量
[0059]
计算上述三角形上三个点的形状函数，该形状函数的表达式为h
l
(u,v)＝c
l,1
+c
l,2
u+c
l,3
v，以点p1的形状函数h1(u,v)＝c
1,1
+c
1,2
u+c
1,3
v为例，它只在p1处取值为1，在其他地方取值为0。
[0060]
所以可获得以下方程组
[0061]
求解得到得到点p1的形状函数h1(u,v)＝1-u-v。
[0062]
同理可得到点p2的形状函数h2(u,v)＝v，点p3的形状函数h3(u,v)＝u。
[0063]
考虑曲面上普通点p1(x1,y1,z1)、p2(x2,y2,z2)、p3(x3,y3,z3)构成的三角平面，通过表面参数化将普通点坐标转换为特殊坐标：
[0064]
p(u,v)＝(x1+u(x
3-x1)+v(x
2-x1),y1+u(y
3-y1)+v(y
2-y1),z1+u(z
3-z1)+v(z
2-z1))。
[0065]
其中0≤u≤1,0≤v≤1,u+v≤1，平面度量张量分量得到
[0066]
此时a、b矩阵变为：
[0067][0068]
[0069]
将上述a、b矩阵代入au＝λbu，即可计算得到拉普拉斯-贝尔特拉米谱。
[0070]
得到拉普拉斯-贝尔特拉米谱后，执行步骤s24、选择每个点云数据的拉普拉斯-贝尔特拉米谱中前若干个值的平均值作为点云数据对应工件表面的曲面特征数据，在本实施例中，选择前50个值的平均值。
[0071]
基于上述q1-q10的点云数据，所得到的拉普拉斯-贝尔特拉米谱分别为0.005069837、0.005092308、0.005114155、0.00513565、0.00513565、0.005227028、0.005274232、0.00531914、0.005913554、0.005913554。
[0072]
步骤s2的拉普拉斯-贝尔特拉米谱计算完成后，执行步骤s3、将点云数据以若干种不同的尺寸分割为分块点云，在本实施例中，分割以5
×
5mm、10
×
10mm、15
×
15mm、20
×
20mm、25
×
25mm、30
×
30mm、35
×
35mm、40
×
40mm、45
×
45mm、50
×
50mm为分割尺寸。
[0073]
s4、计算分块点云中全部任意两块点群之间的最小测地线距离，并将全部的最小测地线距离数据构建成空间测地线距离矩阵。
[0074]
具体的，在计算每个块之间的最小测地线距离时采用每个点群的质心作为特征点，采用点群质心之间的距离作为点群距离。
[0075]
s5、根据上述空间测地线距离矩阵中的最小测地线距离数据计算每个分块点云的greary’s g指数，各个尺寸的分块点云的greary’s g指数如图2所示，使用如下方法计算：
[0076]
其中n为点云的分块数，w
ij
为测地线距离矩阵，i,j是点云中任意两个块的索引，xi,xj分别为第i块，第j块点云的集聚度；分别为第i块，第j块点云的集聚度；是整片点云的集聚度。
[0077]
另外，为了进一步筛查空间相关性显著的分块点云，在步骤s5之后还包括步骤s51、计算每个分块点云的z检验值，并删除z检验值低于预设值的分块尺寸，其中，z检验值当z检验值大于1.96时认为该分块点云的空间相关性显著，删除z检验值小于1.96的分块点云。
[0078]
s6、选择greary’s g指数最低的分块点云的尺寸作为统计尺寸，并根据统计尺寸计算每个分块点云的集聚度。在上述实例的q1-q10曲面中，选择greary’s g指数最小的分块尺寸，即15
×
15mm来计算分块点云的集聚度。
[0079]
集聚度使用如下方法计算：
[0080]
其中n、m指整片点云的尺寸为n
×
m，n、m指点云分块后每个小块的尺寸为n
×
m，n
t
为点云所有点数，bd表示有点落在其中的小分块个数，b
t
表示总分块数，v
ij
指点云分块后每个小块内的点数，其中i,j表示分块索引，即位于点云中第i行j列的小分块。
[0081]
计算得到拉普拉斯-贝尔特拉米谱和集聚度之后，执行步骤s7、根据集聚度及拉普拉斯-贝尔特拉米谱计算每个分块点云的hotelling’s t2统计量。
[0082]
具体的，hotelling’s t2统计量其中n为样本量，为第t个样本的样本均值，μ0和为受控状态下均值向量和协方差矩阵。
[0083]
最后执行步骤s8、根据hotelling’s t2统计量检测存在异常曲面分块点云，具体的，检测以如下方法进行：
[0084]
s81、根据hotelling’s t2统计量生成如图3所示的hotelling’s t2控制图；
[0085]
s82、根据图3的hotelling’s t2控制图找到异常点，从而检测存在异常曲面的分块点云，在图3中根据折线检测出q9、q10为异常曲面。
[0086]
应当说明的是，上述实施例仅是对本发明的优选实施例及原理进行了详细说明，对本领域的普通技术人员而言，依据本发明提供的思想，在具体实施方式上会有改变之处，而这些改变也应视为本发明的保护范围。