光自旋轨道相互作用的调节方法及系统

1.本发明涉及纳米光子技术领域，尤其涉及一种光自旋轨道相互作用的调节方法及系统。


背景技术：

2.自旋轨道相互作用指光子的自旋角动量(对应于经典理论中的圆偏振态)和轨道角动量(对应于经典理论中的角向相位梯度)之间相互转化。圆偏振光正入射到一个反射式的半波片后，其反射场的偏振态将转换为其正交偏振；当该半波片绕其主轴旋转时，反射正交偏振的相位也随之发生线性变化，这种相位变化与波长无关，仅与波片旋转角度有关，因此被称为几何相位。基于几何相位，可实现几何外形与电磁外形解耦。通过光子的自旋轨道相互作用实现局域相位调控。
3.近年来,随着对光的自旋-轨道相互作用相关研究的发展,基于几何相位理论可以提供更多的自由度对光场进行调控。具有更加多样化偏振态分布的矢量光场的出现丰富了矢量光场的种类,并提供了新的调控自由度,因此被应用于光场调控、光学微加工、光学微操纵和光信息传输等领域。在线性光学过程中，自旋角动量到轨道角动量的转换与入射光强度无关。相反，在非线性光学过程中，自旋轨道相互作用可以通过调节光的输入强度来控制。非线性在光学角动量的应用中显示出巨大的潜力。此外，非线性波中的等离子体超表面证明了高阶非线性自旋轨道相互作用。但现有对光自旋轨道相互作用进行调节通常都是通过改变颗粒的形状、大小或者是拓扑粒子，这些调节方法步骤比较复杂、灵活性不够高，因此，亟需一种新的调节方法解决上述问题。


技术实现要素：

4.为此，本发明实施例提供了一种光自旋轨道相互作用的调节方法及系统，用于解决现有技术中调节光自旋轨道相互作用的方法步骤比较复杂、灵活性不够高的问题。
5.为解决上述技术问题，本发明提供了一种光自旋轨道相互作用的调节方法，该方法包括：
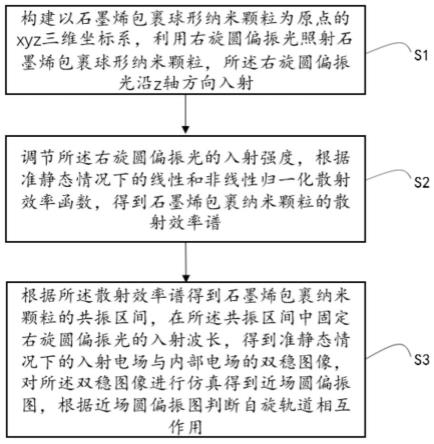
6.s1：构建以石墨烯包裹球形纳米颗粒为原点的xyz三维坐标系，利用右旋圆偏振光照射石墨烯包裹球形纳米颗粒，所述右旋圆偏振光沿z轴方向入射；
7.s2：调节所述右旋圆偏振光的入射强度，根据准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱；
8.s3：根据所述散射效率谱得到石墨烯包裹纳米颗粒的共振区间，在所述共振区间中固定右旋圆偏振光的入射波长，得到准静态情况下的入射电场与内部电场的双稳图像，对所述双稳图像进行仿真得到近场圆偏振图，根据近场圆偏振图判断自旋轨道相互作用。
9.在本发明的一个实施例中，步骤s2中，所述右旋圆偏振光的入射强度表示为：
10.11.其中，e0表示纳米颗粒的局域场，i表示虚数单位,表示x方向的单位向量，表示y方向的单位向量，表示波数，ω表示角频率，λ表示波长，εh表示背景介质的介电常数，z表示xyz三维坐标系中的z轴，t表示时间。
12.在本发明的一个实施例中，所述准静态情况下的线性和非线性归一化散射效率函数的求解方法包括以下步骤：
13.s21：求解拉普拉斯方程在石墨烯界面处的通解，基于纳米颗粒表面的石墨烯层是一个导电率σ的导电壳层，得到边界条件；
14.s22：根据所述通解和所述边界条件求解出未知系数a、b；
15.s23：基于石墨烯的表面电导率是与场相关并且是非线性的特性，得到石墨烯的表面电导率的随机相位近似下的简化形式；
16.s24：根据准静态近似，结合未知系数a、b和简化形式，得到纳米颗粒内部的局域电场和外部电场的关系,并得到准静态情况下的线性和非线性归一化散射效率函数。
17.在本发明的一个实施例中，步骤s21中，所述拉普拉斯方程在石墨烯界面处的通解为：
[0018][0019][0020]
其中，φc表示纳米颗粒内部的电势，φh表示纳米颗粒外的电势，a表示系数，e0表示纳米颗粒的局域场，r表示纳米颗粒的半径，i表示虚数单位，θ表示该点与坐标原点的连线和电场x分量之间的夹角，θ
′
表示该点与坐标原点的连线和电场y分量之间的夹角。
[0021]
在本发明的一个实施例中，步骤s21中，所述边界条件表示如下：
[0022][0023][0024]
其中，eh、dh分别表示纳米颗粒外部的电场和电位移矢量，ec、dc分别表示纳米颗粒内部的线性局域场和电位移矢量，表示纳米颗粒的半径表面散度，j＝σe＝σec表示电流密度矢量，r表示纳米颗粒的半径，表示石墨烯和外部分界面法线方向的单位矢量。
[0025]
在本发明的一个实施例中，步骤s22中，所述未知系数a、b表示如下：
[0026][0027][0028]
其中，θ＝iσ/(ωaε0),i表示虚数单位，σ表示电导率，ε表示相对介电常数，εh表示背景介质的介电常数，ε0表示真空介电常数，ω表示角频率，a表示纳米颗粒的半径，a表示系数，b表示石墨烯包裹的球体的偶极化率。
[0029]
在本发明的一个实施例中，步骤s23中，所述石墨烯的表面电导率的随机相位近似
下的简化形式表示如下：
[0030][0031]
其中，ec表示纳米颗粒内部的线性局域场，σg表示石墨烯线性电导率，σ3表示石墨烯三阶非线性电导率，e，ef，τ分别表示电子电荷量，约化普朗克常数，费米能级，光电子弛豫时间，i表示虚数单位，ω表示角频率，υf表示费米速度；
[0032]
由此可知石墨烯表面电导率的非线性项是跟场紧密相关的，但是非线性电导率σ3远小于线性电导率σg，因此为了能够观察到石墨烯的非线性效应，石墨烯内部电场强度必须很大。而表面等离激元共振可以使局域场增强，从而增大本来很弱的非线性效应。
[0033]
在本发明的一个实施例中，步骤s24中，所述纳米颗粒内部的线性局域电场和外部电场的关系表示如下：
[0034][0035]
其中，ec表示纳米颗粒内部的线性局域场，e0表示纳米颗粒的局域场，ε＝2.25表示相对介电常数，εh表示背景介质的介电常数，ε0表示真空介电常数，σg表示石墨烯线性电导率，i表示虚数单位，ω表示角频率，a表示纳米颗粒的半径。
[0036]
在本发明的一个实施例中，步骤s24中，所述准静态情况下的线性和非线性归一化散射效率函数表示如下：
[0037][0038]
其中，λ表示入射波长，εh表示背景介质的介电常数，i表示虚数单位，a为纳米颗粒的半径，位，a为纳米颗粒的半径，α表示辐射校正过的电极化率，α0表示石墨烯包裹纳米球的电极化率，ε表示相对介电常数，εh表示背景介质的介电常数，θ＝iσ/(ωaε0)，σ表示电导率，ω表示角频率，ε0表示真空介电常数。
[0039]
本发明还提供了一种光自旋轨道相互作用的调节系统，该系统包括：
[0040]
入射模块，用于构建以石墨烯包裹球形纳米颗粒为原点的xyz三维坐标系，利用右旋圆偏振光照射石墨烯包裹球形纳米颗粒，所述右旋圆偏振光沿z轴方向入射；
[0041]
调节模块，用于调节所述右旋圆偏振光的入射强度，根据准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱；
[0042]
输出模块，用于根据所述散射效率谱得到石墨烯包裹纳米颗粒的共振区间，在所述共振区间中固定右旋圆偏振光的入射波长，得到准静态情况下的入射电场与内部电场的双稳图像，对所述双稳图像进行仿真得到近场圆偏振图，根据近场圆偏振图判断自旋轨道相互作用。
[0043]
本发明的上述技术方案相比现有技术具有以下优点：
[0044]
本发明提供了一种光自旋轨道相互作用的调节方法及系统，通过调节入射光的强
度，实现了对光自旋轨道相互作用的调节；通过求解得到石墨烯包裹纳米颗粒在准静态情况下的线性和非线性归一化散射效率函数，将三维石墨烯包裹纳米颗粒在圆偏振光入射下的散射效率推导方法从mie理论拓展到准静态理论；利用石墨烯的双稳特性可以调节远场的散射效率和近场的自旋轨道相互作用；通过右旋圆偏振光照射石墨烯包裹球形纳米颗粒，利用石墨烯光学非线性的高度可调节性，为灵活调节光自旋轨道相互作用提供了一种有效并且方便的方法。
附图说明
[0045]
为了更清楚地说明本发明实施案例或现有技术中的技术方案，下边将对实施例中所需要使用的附图做简单说明，通过参考附图会更清楚的会理解本发明的特征和优点，附图是示意性的而不应该理解为对本发明进行任何限制，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，可以根据这些附图获得其他的附图。其中：
[0046]
图1是根据本发明实施例中一种光自旋轨道相互作用的调节方法的流程示意图；
[0047]
图2是根据本发明实施例中石墨烯包裹的纳米颗粒在右圆偏振光入射下的模型示意图；
[0048]
图3中(a)是根据本发明实施例中准静态近似(连续线)和有限元法(点线)得到的线性和非线性在右旋圆偏振光入射的归一化散射效率示意图；(b)是根据本发明实施例中圆偏振光和右旋偏振光入射时纳米颗粒内部电场随入射场的示意图；
[0049]
图4中(a)-(c)是xp光入射局域电场在x-y、y-z和x-z平面的分布的示意图，(d)-(f)为rcp光入射局域电场在x-y、y-z和x-z平面的分布的示意图；
[0050]
图5是根据本发明实施例中在有限元rcp光入射时，内场与外部入射场e0的关系示意图；
[0051]
图6是根据本发明实施例中一种光自旋轨道相互作用的调节系统的框图示意图。
具体实施方式
[0052]
为使得本发明的发明目的、特征、优点能够更加的明显和易懂，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，下面所描述的实施例仅仅是本发明一部分实施例，而非全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。
[0053]
参照图1所示，本发明实施例提供了一种光自旋轨道相互作用的调节方法，该方法包括：
[0054]
s1：构建以石墨烯包裹球形纳米颗粒为原点的xyz三维坐标系，利用右旋圆偏振光照射石墨烯包裹球形纳米颗粒，所述右旋圆偏振光沿z轴方向入射；
[0055]
s2：调节所述右旋圆偏振光的入射强度，根据准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱；
[0056]
s3：根据所述散射效率谱得到石墨烯包裹纳米颗粒的共振区间，在所述共振区间中固定右旋圆偏振光的入射波长，得到准静态情况下的入射电场与内部电场的双稳图像，对所述双稳图像进行仿真得到近场圆偏振图，根据近场圆偏振图判断自旋轨道相互作用。
[0057]
本发明通过右旋圆偏振光照射石墨烯包裹球形纳米颗粒，利用石墨烯的高度可调性使得在实际操作中更易调节光的自旋轨道相互作用；通过求解得到石墨烯包裹纳米颗粒在准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱，有利于找到石墨烯包裹纳米颗粒的共振区间；通过comsol软件对获得的双稳图像进行仿真，得到近场圆偏振图，实现对自旋轨道相互作用的调节。本发明通过调节入射光的强度，实现了对光自旋轨道相互作用的调节，为灵活调节光自旋轨道相互作用提供了一种有效并且方便的方法。
[0058]
进一步地，在步骤s1中：
[0059]
如图2所示，构建以石墨烯包裹球形纳米颗粒为原点的xyz三维坐标系，利用右旋圆偏振光照射石墨烯包裹球形纳米颗粒，所述右旋圆偏振光沿z轴方向入射；通过右旋圆偏振光照射石墨烯包裹球形纳米颗粒，利用石墨烯的高度可调性使得在实际操作中更易调节光的自旋轨道相互作用。
[0060]
进一步地，在步骤s2中：
[0061]
调节所述右旋圆偏振光的入射强度，根据准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱；通过求解得到石墨烯包裹纳米颗粒在准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱，有利于找到石墨烯包裹纳米颗粒的共振区间，同时也实现了将三维石墨烯包裹纳米颗粒在圆偏振光入射下的散射效率推导方法从mie理论拓展到准静态理论。
[0062]
本发明实施例中右旋圆偏振光入射强度为：
[0063][0064]
其中，e0表示纳米颗粒的局域场，i表示虚数单位,表示x方向的单位向量，表示y方向的单位向量，表示波数，ω表示角频率，λ表示波长，εh表示背景介质的介电常数，z表示xyz三维坐标系中的z轴，t表示时间；
[0065]
所述准静态情况下的线性和非线性归一化散射效率函数的求解方法包括以下步骤：
[0066]
s21：求解拉普拉斯方程在石墨烯界面处的通解，基于纳米颗粒表面的石墨烯层是一个导电率σ的导电壳层，得到边界条件；
[0067]
s22：根据所述通解和所述边界条件求解出未知系数a、b；
[0068]
s23：基于石墨烯的表面电导率是与场相关并且是非线性的特性，得到石墨烯的表面电导率的随机相位近似下的简化形式；
[0069]
s24：根据准静态近似，结合未知系数a、b和简化形式，得到纳米颗粒内部的局域电场和外部电场的关系,并得到准静态情况下的线性和非线性归一化散射效率函数。
[0070]
在步骤s21中，所述拉普拉斯方程在石墨烯界面处的通解为：
[0071][0072][0073]
其中，φc表示纳米颗粒内部的电势，φh表示纳米颗粒外的电势，a表示系数，e0表
示纳米颗粒的局域场，r表示纳米颗粒的半径，i表示虚数单位，θ表示该点与坐标原点的连线和电场x分量之间的夹角，θ
′
表示该点与坐标原点的连线和电场y分量之间的夹角。
[0074]
在步骤s21中，所述边界条件表示如下：
[0075][0076][0077]
其中，eh、dh分别表示纳米颗粒外部的电场和电位移矢量，ec、dc分别表示纳米颗粒内部的线性局域场和电位移矢量，表示纳米颗粒的半径表面散度，j＝σe＝σec表示电流密度矢量，r表示纳米颗粒的半径，表示石墨烯和外部分界面法线方向的单位矢量。
[0078]
在步骤s22中，所述未知系数a、b表示如下：
[0079][0080][0081]
其中，θ＝iσ/(ωaε0),i表示虚数单位，σ表示电导率，ε表示相对介电常数，εh表示背景介质的介电常数，ε0表示真空介电常数，ω表示角频率，a表示纳米颗粒的半径，a表示系数，b表示石墨烯包裹的球体的偶极化率。
[0082]
在步骤s23中，所述石墨烯的表面电导率的随机相位近似下的简化形式表示如下：
[0083][0084]
其中，ec表示纳米颗粒内部的线性局域场，σg表示石墨烯线性电导率，σ3表示石墨烯三阶非线性电导率，e，ef，τ分别表示电子电荷量，约化普朗克常数，费米能级，光电子弛豫时间，i表示虚数单位，ω表示角频率，υf表示费米速度。
[0085]
在步骤s24中，所述纳米颗粒内部的线性局域电场和外部电场的关系表示如下：
[0086][0087]
其中，ec表示纳米颗粒内部的线性局域场，e0表示纳米颗粒的局域场，ε＝2.25表示相对介电常数，εh表示背景介质的介电常数，ε0表示真空介电常数，σg表示石墨烯线性电导率，i表示虚数单位，ω表示角频率，a表示纳米颗粒的半径。
[0088]
所述准静态情况下的线性和非线性归一化散射效率函数表示如下：
[0089][0090]
其中，λ表示入射波长，εh表示背景介质的介电常数，i表示虚数单
位，a为纳米颗粒的半径，位，a为纳米颗粒的半径，α表示辐射校正过的电极化率，α0表示石墨烯包裹纳米球的电极化率，ε表示相对介电常数，εh表示背景介质的介电常数，θ＝iσ/(ωaε0)，σ表示电导率，ω表示角频率，ε0表示真空介电常数。
[0091]
进一步地，在步骤s3中：
[0092]
根据所述散射效率谱得到石墨烯包裹纳米颗粒的共振区间，在所述共振区间中固定右旋圆偏振光的入射波长，得到准静态情况下的入射电场与内部电场的双稳图像，通过使用comsol软件对所述双稳图像进行仿真得到近场圆偏振图，根据近场圆偏振图判断自旋轨道相互作用。
[0093]
本发明通过调节入射光的强度，实现了对光自旋轨道相互作用的调节，为灵活调节光自旋轨道相互作用提供了一种有效并且方便的方法。
[0094]
下面结合附图与实施例对本发明作进一步说明。
[0095]
实施例中，石墨烯包裹纳米颗粒半径为50nm，粒子的相对介电常数为2.25，入射波长为13.5nm。
[0096]
如图3所示，在图3(a)中显示了归一化散射效率q
sca
与入射波长λ的关系。连续曲线分别对应于不同入射电场值的qsa的线性(linear)和非线性(nonlinear)的解:e0＝0.5mev和e0＝1.5mev。散射效率曲线中的共振峰是由于在太赫兹频率石墨烯层表现出金属的特性，这清楚地表明石墨烯在电导率上的类似克尔非线性通常会导致共振峰的红移和共振强度的降低。这是由于当入射光强度增加时，克尔型金属非线性的本征波长将发生红移。相比结果通过有限元方法(fem)与qsa,结果有限元非常类似于qsa但存在些许的不同。这是由于准静态极限的理论逼近，而在有限元中没有应用。在有限元中，当计算石墨烯的表面电流密度和非线性表面电导率时，使用石墨烯表面的局域电场，而不是纳米颗粒内部的电场，即j＝σe
local
和当光场较高时(e0＝1.5mev)，观察到光学双稳响应，在指定波长处有两个稳定的分支和一个突变的切换效应。
[0097]
在图3(b)中分别为xp光和rcp光在qsa和fem中的ec和入射场e0的光学双稳响应。从图中可以得到，在适当的入射电场范围内，存在双稳态响应，当入射场从较低的值(即e0＝0.8mev)增加时，纳米颗粒内部电场ec先增加，然后在开关阈值场e
0，up
处跃迁到上稳定支路；之后，电场ec随入射场单调增大；反之，当入射场从较高的值(即e0＝0.8mev)下降时，电场ec会在切换阈值场e
0，down
处不连续地跳到较低的稳定支路。需要注意的是，图中的虚线代表了计算出的不稳定分支，这是非线性问题的数学解，但在实际操作中是不存在的。从图3(b)，观察到，对于线偏振光(xp形式为观察到，对于线偏振光(xp形式为)和圆偏振光，qsa方法计算的内部电场ec和入射电场e0之间的关系是相同的。这是因为在准静态极限下，石墨烯包裹纳米颗粒的极化率与入射极化率无关。而用有限元法计算，结果有显著差异。更重要的是，对于两种极化波，基于fem计算的阈值场均小于qsa计算的结果。我们有理由推测这是因为qsa只考虑了内场ec，实际上边界处的电场得到了有效的增强，而这在计算中被忽略了。
[0098]
如图4所示，rcp波比xp波需要更小的阈值场，因为它们在石墨烯表面激发了更强的局域场和更大的增强区，所有的图都是用fem计算的，并且共享相同的颜色条。
[0099]
如图5所示，在有限元rcp入射时，内场与外部入射场e0的关系。插入(i～iv)为不
同位置近场的圆极化度(cpd)的分布，它们共享同一个颜色条，颜色范围归一化，插图是两个稳定分支中不同位置(标记为i、ii、iii、iv)近场的cpd分布，其中位置ii和位置iv的入射场强度相同(0.93mev)。这里，定义cpd为|ε0e
*
×
e+μ0h
*
×
h|/(ε0|e0|2+μ0|h|2)，实现cpd＝1的圆偏振。根据双稳态响应的特点，i
→
ii
→
iii和iii
→
iv
→
i分别通过切换上支和切换下支。首先，着重研究了入射场逐渐增大的过程，值得注意的是，由于点i和点ii都在较低的稳定分支中，它们得到了几乎相同的结果。同时，在阈值字段e
0，up
处发生突发性不连续跳跃后，iii位置处cpd跳转到较高的值。与位置ii的场相比，位置iii的高cpd意味着光子的大部分轨道角动量(oam)通过该区域的自旋轨道相互作用转换为自旋角动量(sam)。同理，当外加的场不断减小时，位置(iii-iv)的cpd先保持不变，然后在阈值场处突然不连续跳变e
0，down
后，cpd下降到较低的值。相反，与位置iv的场相比，位置i的低cpd意味着大部分光子的sam通过自旋轨道相互作用转换为oam。有趣的是，虽然ii和iv位置的入射场强相同，但cpd的分布却有很大的不同。
[0100]
本发明提出的光自旋轨道相互作用的调节方法，通过调节入射光的强度，实现了对光自旋轨道相互作用的调节；利用石墨烯的双稳特性可以调节远场的散射效率和近场的自旋轨道相互作用；通过右旋圆偏振光照射石墨烯包裹球形纳米颗粒，利用石墨烯光学非线性的高度可调节性，为灵活调节光自旋轨道相互作用提供了一种有效并且方便的方法。
[0101]
参照图6所示，本发明实施例提供了一种光自旋轨道相互作用的调节系统，该系统包括入射模块610、调节模块620以及输出模块630；
[0102]
所述入射模块610，用于构建以石墨烯包裹球形纳米颗粒为原点的xyz三维坐标系，利用右旋圆偏振光照射石墨烯包裹球形纳米颗粒，所述右旋圆偏振光沿z轴方向入射；
[0103]
所述调节模块620，用于调节所述右旋圆偏振光的入射强度，根据准静态情况下的线性和非线性归一化散射效率函数，得到石墨烯包裹纳米颗粒的散射效率谱；
[0104]
所述输出模块630，用于根据所述散射效率谱得到石墨烯包裹纳米颗粒的共振区间，在所述共振区间中固定右旋圆偏振光的入射波长，得到准静态情况下的入射电场与内部电场的双稳图像，对所述双稳图像进行仿真得到近场圆偏振图，根据近场圆偏振图判断自旋轨道相互作用。
[0105]
该系统用以实现上述所述的一种光自旋轨道相互作用的调节方法，为了避免冗余，在此不再赘述。
[0106]
本领域内的技术人员应明白，本技术的实施例可提供为方法、系统、或计算机程序产品。因此，本技术可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本技术可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。
[0107]
本技术是参照根据本技术实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0108]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0109]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0110]
显然，上述实施例仅仅是为清楚地说明所作的举例，并非对实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式变化或变动。这里无需也无法对所有的实施方式予以穷举。而由此所引申出的显而易见的变化或变动仍处于本发明创造的保护范围之中。