基于残差克里金法的电磁频谱地图构建方法、装置和设备

1.本技术涉及电磁频谱监测技术领域，特别是涉及一种基于残差克里金法的电磁频谱地图构建方法、装置和设备。


背景技术：

2.电磁频谱地图（spectrum map）也被称之为无线电环境地图（radio environment map）或无线电地图（radio map），可从时间、空间、频率和能量等多个维度对电磁环境进行定量描述，并结合地理信息系统进行可视化展示。电磁频谱地图为电磁空间认知与控制利用等诸多军民应用提供基础信息，其用途主要有四个方面，一是获取电磁频谱资源分布状况，支撑频谱资源精细化动态分配，实现电磁频谱资源高效利用；二是获取电磁辐射分布状况，为电磁污染监测与防治提供量化依据。三是获取电磁干扰行为规律，支撑黑广播、伪基站等违法行为查处，维护用频秩序；四是军事应用领域，电磁频谱地图可为电磁态势生成、装备部署运用、作战用频规划和用频冲突消解等应用提供辅助决策信息。因此，准确、快速构建电磁频谱地图具有十分重要的意义。
3.根据是否需要辐射源与传播模型等先验信息，电磁频谱地图构建方法通常分为直接构建法、间接构建法和混合构建法三类。直接构建法主要包括最近邻法、自然邻点法、反距离加权法、样条法、改进shepard法和梯度距离平方反比法等确定性插值法和克里金法等地统计学变分插值法。间接构建法需利用辐射源和传播模型等先验信息，主要包括基于完备先验信息的正演法、基于发射机位置估计法、接收信号强度差分法和信噪比辅助法等。混合构建法将直接构建法和间接构建法相结合，包括基于图像处理的混合构建法、利用克里金法对传播模型构建结果进行修正的混合构建法和基于多中心幂函数拟合的混合构建法等。实际应用中，由于先验信息无法全部获得，对先验信息依赖性较强的间接构建法的适用范围受限。而直接构建法因为无法利用已获得的部分先验信息，导致构建精度不高。如何提出一个混合构建方法可以利用部分先验信息，在提高算法适用性与鲁棒性的同时提高构建精度成为了当前电磁频谱地图构建中的关键问题。


技术实现要素：

4.基于此，有必要针对上述技术问题，提供一种基于残差克里金法的电磁频谱地图构建方法、装置和设备。
5.一种基于残差克里金法的电磁频谱地图构建方法，所述方法包括：获取电磁环境监测数据以及待估计点位置，所述电磁环境监测数据包括位置信息和对应位置的接收功率。
6.根据模型参数的先验分布和根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布。
7.根据所述模型参数的后验分布，采用吉布斯采样方式，得到模型参数估计值。
8.根据所述模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估
计值。
9.将所述接收功率与对应位置的所述路径衰减分量估计值作差，得到残差监测数据。
10.根据所述残差监测数据，采用指数模型的残差克里金插值方法，得到待估计点位置的阴影衰落分量估计值。
11.将所述路径衰减分量估计值和所述阴影衰落分量估计值求和，得到待估计点位置的接收功率估计值。
12.一种基于残差克里金的电磁频谱地图构建装置，所述装置包括：电磁环境监测数据获取模块：用于获取电磁环境监测数据以及待估计点位置，所述电磁环境监测数据包括位置信息和对应位置的接收功率。
13.路径衰减分量估计值确定模块，用于根据模型参数的先验分布和根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布；根据所述模型参数的后验分布，采用吉布斯采样方式，得到模型参数估计值；根据所述模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估计值。
14.阴影衰落分量估计值确定模块，用于将所述接收功率与对应位置的所述路径衰减分量估计值作差，得到残差监测数据；根据所述残差监测数据，采用指数模型的残差克里金插值，得到待估计点位置的阴影衰落分量估计值。
15.估计结果确定模块，用于将所述路径衰减分量估计值和所述阴影衰落分量估计值求和，得到待估计点位置的接收功率估计值。
16.一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述处理器执行所述计算机程序时实现上述任一所述方法的步骤。
17.上述基于残差克里金法的电磁频谱地图构建方法、装置和设备，该方法根据电波传播理论将电磁频谱地图构建分解为路径衰减和阴影衰落分量的估计，首先基于路径衰减模型参数的先验分布，以及监测数据构成的似然，通过贝叶斯定理构建贝叶斯层级模型，得到模型参数的后验分布，根据模型参数的后验分布采用吉布斯采样的方法获得模型参数的估计值，从而实现路径衰减的估计；然后将监测数据与对应位置的路径衰减分量估计值作差，得到残差监测数据，再通过克里金插值进行阴影衰落分量估计。本方法将贝叶斯层级模型和残差克里金法两者结合，达到提高方法的适用性、鲁棒性的同时完成电磁频谱地图的高精度构建。
附图说明
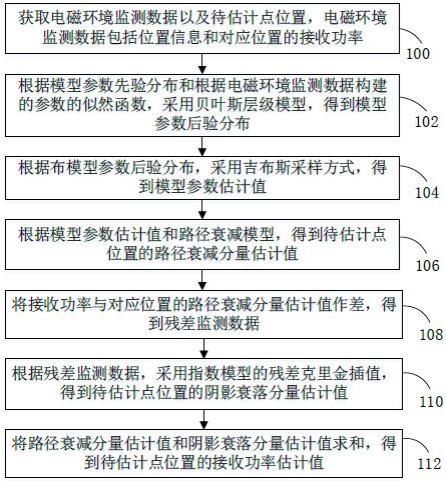
18.图1为一个实施例中基于残差克里金法的电磁频谱地图构建方法的流程示意图；图2为另一个实施例中贝叶斯层级模型；图3为另一个实施例中不同监测数据量条件下均方根误差对比；图4为另一个实施例中不同阴影衰落标准偏差条件下均方根误差对比；图5为一个实施例中基于残差克里金的电磁频谱地图构建装置的结构框图；图6为一个实施例中计算机设备的内部结构图。
具体实施方式
19.为了使本技术的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本技术进行进一步详细说明。应当理解，此处描述的具体实施例仅仅用以解释本技术，并不用于限定本技术。
20.在一个实施例中，如图1所示，提供了一种基于残差克里金法的电磁频谱地图构建方法，该方法包括以下步骤：步骤100：获取电磁环境监测数据以及待估计点位置，电磁环境监测数据包括位置信息和对应位置的接收功率。
21.具体的，获取感兴趣区域内有限数量电磁环境监测数据，包括接收功率及其位置信息，两者分布可以用向量形式表示为和，估计区域内任意位置处的接收功率，是电磁环境监测数据的数量，其取值范围为大于1的整数。
22.步骤102：根据模型参数的先验分布和根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布。
23.具体的，路径衰减模型为：（1）其中，为信号源辐射功率, 为信号源位置, 为路径衰减指数, 为与之间的距离，为天线远场参考距离, 为路径衰减因子, 是一个关于辐射信号工作波长的函数。
24.阴影衰落满足于gudmundson模型，其空间相关性可表示为：（2）其中，为阴影衰落标准偏差，为解相关距离。但在实际中，由于监测站点往往分散地分布在区域内，两两之间的距离远比解相关距离要大，故而相关性可进一步近似为。
25.根据模型参数的先验知识设计模型参数的先验分布，根据电磁环境监测数据构建模型参数的似然函数，根据贝叶斯理论，模型参数的后验估计满足：（3）其中，，为信号源辐射功率、为路径衰减指数，为阴影衰落标准偏差，为电磁环境监测数据。
26.根据模型参数的先验分布和模型参数的似然函数，根据如图2所示的模型参数的贝叶斯层级模型进行推导，得到模型参数的后验分布。
27.因此，电磁环境监测数据的均值和方差可表示为：（4）（5）其中，为单位矩阵。
28.步骤104：根据模型参数的后验分布，采用吉布斯采样方式，得到模型参数估计值。
29.具体的，根据模型参数的后验分布，通过使用基于吉布斯采样的贝叶斯层级模型，对模型参数求解，提升电磁地图构建精度。
30.获得了参数的后验分布后，传统方法是通过积分获得参数的估计。但在工程实际中并非所有的参数分布形式都可以获得闭合解，为提高算法适用性与鲁棒性，本发明使用了吉布斯采样对参数估计进行数值求解。
31.步骤106：根据模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估计值。
32.步骤108：将接收功率与对应位置的路径衰减分量估计值作差，得到残差监测数据。
33.具体的，残差监测数据的表达式为：（6）其中，为位置处的残差监测数据，为位置处的接收功率，为位置处的路径衰减分量估计。
34.步骤110：根据残差监测数据，采用指数模型的残差克里金插值方法，得到待估计点位置的阴影衰落分量估计值。
35.具体的，基于监测数据的残差值，满足地统计学前提条件，通过指数模型的残差克里金法求解，提升构建精度。
36.步骤112：将路径衰减分量估计值和阴影衰落分量估计值求和，得到待估计点位置的接收功率估计值。
37.具体的，将电磁频谱地图构建分解为路径衰减和阴影衰落分量的估计，提升电磁地图构建精度。
38.电磁频谱地图的构建可表示为路径衰减与阴影衰落两个分量估计之和：（7）其中，为位置处的残差监测数据估计值，为待估计点位置的接收功率估计值，为位置处的路径衰减分量估计。
39.上述基于残差克里金法的电磁频谱地图构建方法中，根据电波传播理论将电磁频
谱地图构建分解为路径衰减和阴影衰落分量的估计，首先基于路径衰减模型参数的先验分布，以及监测数据构成的似然，通过贝叶斯定理构建贝叶斯层级模型，得到模型参数的后验分布，根据模型参数的后验分布采用吉布斯采样的方法获得模型参数的估计值，从而实现路径衰减的估计；然后将监测数据与对应位置的路径衰减分量估计值作差，得到残差监测数据，再通过克里金插值进行阴影衰落分量估计。本方法将贝叶斯层级模型和残差克里金法两者结合，达到提高方法的适用性、鲁棒性的同时完成电磁频谱地图的高精度构建。
40.在其中一个实施例中，模型参数包括：信号源辐射功率，路径衰减指数以及阴影衰落标准偏差；步骤102具体包括如下步骤：步骤200：根据信号源辐射功率的取值范围，采用正态分布模型设计信号源辐射功率的先验分布。
41.（8）作为优选，信号源辐射功率的先验分布的均值的取值范围21~39dbm，信号源辐射功率的先验分布的方差的取值4。
42.步骤202：根据路径衰减指数的取值范围，采用正态分布模型设计路径衰减指数的先验分布。
43.（9）作为优选，路径衰减指数的先验分布的均值取值范围1.0~5.0，路径衰减指数的先验分布的方差的取值为4。
44.步骤204：根据阴影衰落标准偏差的取值范围，采用逆伽玛分布模型设计阴影衰落标准偏差的先验分布。
45.（10）作为优选，阴影衰落标准偏差的先验分布的形状参数的取值为2，比例参数的取值为1/16。
46.步骤206：根据信号源辐射功率的先验分布、路径衰减指数的先验分布、阴影衰落标准偏差的先验分布以及根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布。
47.在其中一个实施例中，步骤206包括：根据信号源辐射功率的先验分布、路径衰减指数的先验分布、阴影衰落标准偏差的先验分布以及根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到信号源辐射功率的后验分布、路径衰减指数的后验分布以及阴影衰落标准偏差的后验分布。
48.其中，信号源辐射功率的后验分布为：
（11）（12）（13）其中，为信号源辐射功率的后验分布，、分别为信号源辐射功率的后验分布的均值和方差，normal( )为正态分布函数；为信号源辐射功率, 为路径衰减指数，为信号源位置, 为第r个电磁环境监测点位置, 为与之间的距离，为第r个电磁环境监测数据，为天线远场参考距离, 为阴影衰落标准偏差，为路径衰减因子，和为信号源辐射功率的先验分布的均值和方差；r为电磁环境监测数据的数量。
49.路径衰减指数的后验分布为：（14）（15）（16）其中，为路径衰减指数的后验分布，、分别为路径衰减指数的后验分布的均值和方差，和为路径衰减指数的先验分布的均值和方差。
50.阴影衰落标准偏差的后验分布为：（17）（18）
（19）其中，为阴影衰落标准偏差的后验分布，、分别为阴影衰落标准偏差的后验分布的形状参数和比例参数，、分别为阴影衰落标准偏差的先验分布的形状参数和比例参数，inverse gamma( )为逆伽玛分布函数。
51.具体的，参数的后验分布的推导过程如下：根据式（3）和式（8）-（10）对各参数的后验分布进行推导。
52.（1）信号源辐射功率的后验分布为：（1）信号源辐射功率的后验分布为：（1）信号源辐射功率的后验分布为：（1）信号源辐射功率的后验分布为：（20）其中，const为常数。
53.（2）路径衰减指数的后验分布为：（2）路径衰减指数的后验分布为：
（21）（3）阴影衰落标准偏差的后验估计为：估计为：估计为：（22）对式（20）-（22）进行整理，得到如式（14）-（19）所示的信号源辐射功率的后验分布、路径衰减指数的后验分布以及阴影衰落标准偏差的后验分布的表达式。
54.在其中一个实施例中，步骤104包括：设置迭代次数为1；根据信号源辐射功率的后验分布、路径衰减指数的后验分布以及阴影衰落标准偏差的后验分布，生成信号源辐射功率的初始采样值、路径衰减指数的初始采样值以及阴影衰落标准偏差的初始采样值；迭代次数加1；根据信号源辐射功率的后验分布，采用信号源辐射功率的采样公式进行采样；信号源辐射功率的采样公式为：（23）其中，为第n个信号源辐射功率的采样值，为第n-1个路径衰减指数的采样值，为第n-1个阴影衰落标准偏差的采样值，为电磁环境监测数据。
55.根据路径衰减指数的后验分布，采用路径衰减指数采样公式进行采样，路径衰减指数采样公式为：
（24）其中，为第n个路径衰减指数的采样值。
56.根据阴影衰落标准偏差的后验分布，采用阴影衰落标准偏差采样公式进行采样，阴影衰落标准偏差采样公式为：（25）其中，为第n个阴影衰落标准偏差的采样值。
57.继续进行下一轮迭代采样，直到迭代次数等于预设最大迭代次数；在信号源辐射功率、路径衰减指数以及阴影衰落标准偏差的采样值中去除burn-in值后取均值，得到信号源辐射功率、路径衰减指数以及阴影衰落标准偏差的参数估计值。
58.具体的，burn-in值指的是最初采样得到的若干组值。
59.本发明使用了吉布斯采样对参数估计进行数值求解。吉布斯采样的步骤可概述如下1）设置迭代次数与最大迭代次数。
60.2）生成参数初始值，和。
61.3）迭代设置迭代次数。
62.根据式（11）-（13）采样。
63.根据式（14）-（16）采样。
64.根据式（17）-（19）采样。
65.4. 直到迭代次数。
66.在各参数的采样值中去除“burn-in”值后取均值即可作为参数的估计值。
67.在其中一个实施例中，步骤104包括：据模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估计值为：（26）其中，为待估计点位置的路径衰减分量估计值，为信号源辐射功率的估计值，为路径衰减指数的估计值；为信号源位置, 为第k个待估计点位置, 为待估计点位置集合，为与之间的距离，为天线远场参考距离, 为路径衰减因子。
68.在其中一个实施例中，步骤110包括具体包括如下步骤：步骤300：根据阴影衰落分量的空间相关性，采用指数模型作为克里金插值中的变
差函数；克里金插值中的变差函数为：（27）其中，为块金值, 为基台值，为变程。
69.步骤302：根据残差监测数据和监测数据关于未知点的权重，得到阴影衰落分量的表达式为：（28）其中，为第个监测数据关于未知点的权重，满足于。
70.步骤304：根据克里金插值中的变差函数和监测数据关于未知点的权重，构建克里金方程组，并对克里金方程组进行求解，得到监测数据关于未知点的权重。
71.步骤306：根据残差监测数据、监测数据关于未知点的权重以及阴影衰落分量的表达式，得到阴影衰落分量的估计值。
72.具体的，根据克里金插值中的变差函数和监测数据关于未知点的权重，构建的克里金方程组为： (29)其中，为朗格朗日乘子。克里金方程组可被表示为矩阵形式为：.
ꢀꢀꢀ
（30）
在其中一个实施例中，步骤300中阴影衰落分量的空间相关性为：（31）其中，为空间相关性的函数，i、j大于等于1的整数，为与之间的距离，为阴影衰落标准偏差，为解相关距离。
73.在一个验证性实施例中，考虑到电磁态势生成等电磁频谱地图具体应用中，构建精度是电磁频谱地图构建的关键，因此选取均方根误差（rootmeansquare error, rmse）作为评价指标，以应用较为广泛的反距离加权法（inverse distance weighted，idw）、自然邻域法（natural neighbor, nni）、广义回归神经网络（general regression neural network，grnn），普通克里金法（ordinarykriging，ok）以及纯粹贝叶斯模型（bhm）作为参考方法，与本发明方法基于残差克里金法（bhm-rk）进行性能对比分析。
74.图3给出了不同监测数据量条件下本方法与参考方法的均方根误差对比。可以看出：（1）所有方法rmse的整体趋势都随着数据量的增大而减小。表明获取的监测数据越多，电磁频谱地图构建精度越高。（2）在相同的数据量条件下本发明方法的rmse均小于参考方法的表明使用相同数量的监测数据构建电磁频谱地图，本发明方法能获得较参考方法更高的构建精度，且在监测数据的稀疏的情形下，本发明方法在构建精度方面的优势更显著。
75.图4给出了不同阴影衰落标准偏差条件下本发明方法与参考方法的均方根误差对比。可以看出：（1）两种方法的时间成本均随着数据量的增大而增大。表明阴影衰落标准偏差越大，电磁频谱地图构建精度越低。（2）在相同的数据量条件下本发明方法的时间成本均小于参考方法的。表明通过受到同样阴影衰落标准偏差影响的监测数据构建电磁频谱地图，本发明方法能获得较参考方法更高的电磁频谱地图构建精度。
76.上述结果说明，将电磁频谱地图构建分解为路径衰减和阴影衰落分量的估计，分别使用贝叶斯层级模型和残差克里金法求解，可提升电磁频谱地图构建精度。
77.应该理解的是，虽然图1的流程图中的各个步骤按照箭头的指示依次显示，但是这些步骤并不是必然按照箭头指示的顺序依次执行。除非本文中有明确的说明，这些步骤的执行并没有严格的顺序限制，这些步骤可以以其它的顺序执行。而且，图1中的至少一部分步骤可以包括多个子步骤或者多个阶段，这些子步骤或者阶段并不必然是在同一时刻执行完成，而是可以在不同的时刻执行，这些子步骤或者阶段的执行顺序也不必然是依次进行，而是可以与其它步骤或者其它步骤的子步骤或者阶段的至少一部分轮流或者交替地执行。
78.在一个实施例中，如图5所示，提供了一种基于残差克里金的电磁频谱地图构建装置，包括：电磁环境监测数据获取模块、路径衰减分量估计值确定模块、阴影衰落分量估计值确定模块和估计结果确定模块，其中：电磁环境监测数据获取模块：用于获取电磁环境监测数据以及待估计点位置，电磁环境监测数据包括位置信息和对应位置的接收功率。
79.路径衰减分量估计值确定模块，用于根据模型参数的先验分布和根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布；根据
模型参数的后验分布，采用吉布斯采样方式，得到模型参数估计值；根据模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估计值。
80.阴影衰落分量估计值确定模块，用于将接收功率与对应位置的路径衰减分量估计值作差，得到残差监测数据；根据残差监测数据，采用指数模型的残差克里金插值，得到待估计点位置的阴影衰落分量估计值。
81.估计结果确定模块，用于将路径衰减分量估计值和阴影衰落分量估计值求和，得到待估计点位置的接收功率估计值。
82.在其中一个实施例中，模型参数包括：信号源辐射功率，路径衰减指数以及阴影衰落标准偏差；路径衰减分量估计值确定模块，还用于根据信号源辐射功率的取值范围，采用正态分布模型设计信号源辐射功率的先验分布；根据路径衰减指数的取值范围，采用正态分布模型设计路径衰减指数的先验分布；根据阴影衰落标准偏差的取值范围，采用逆伽玛分布模型设计阴影衰落标准偏差的先验分布；根据信号源辐射功率的先验分布、路径衰减指数的先验分布、阴影衰落标准偏差的先验分布以及根据电磁环境监测数据构建的模型参数的似然函数，采用贝叶斯层级模型，得到模型参数的后验分布。
83.在其中一个实施例中，路径衰减分量估计值确定模块，还用于设置迭代次数为1；根据信号源辐射功率的后验分布、路径衰减指数的后验分布以及阴影衰落标准偏差的后验分布，生成信号源辐射功率的初始采样值、路径衰减指数的初始采样值以及阴影衰落标准偏差的初始采样值；迭代次数加1；根据信号源辐射功率的后验分布，采用信号源辐射功率的采样公式进行采样；信号源辐射功率的采样公式如式（23）所示；根据路径衰减指数的后验分布，采用路径衰减指数采样公式进行采样，路径衰减指数采样公式如式（24）所示；根据阴影衰落标准偏差的后验分布，采用阴影衰落标准偏差采样公式进行采样，阴影衰落标准偏差采样公式如式（25）所示；继续进行下一轮迭代采样，直到迭代次数等于预设最大迭代次数；在信号源辐射功率、路径衰减指数以及阴影衰落标准偏差的采样值中去除burn-in值后取均值，得到信号源辐射功率、路径衰减指数以及阴影衰落标准偏差的参数估计值。
84.在其中一个实施例中，路径衰减分量估计值确定模块，还用于根据模型参数估计值和路径衰减模型，得到待估计点位置的路径衰减分量估计值的表达式如式（26）所示。
85.在其中一个实施例中，阴影衰落分量估计值确定模块，还用于根据阴影衰落分量的空间相关性，采用指数模型作为克里金插值中的变差函数；克里金插值中的变差函数如式（27）所示；根据残差监测数据和监测数据关于未知点的权重，得到阴影衰落分量的表达式如式（28）所示；根据克里金插值中的变差函数和监测数据关于未知点的权重，构建克里金方程组，并对克里金方程组进行求解，得到监测数据关于未知点的权重；根据残差监测数据、监测数据关于未知点的权重以及阴影衰落分量的表达式，得到阴影衰落分量的估计值。
86.在其中一个实施例中，根据阴影衰落分量的空间相关性，采用指数模型作为克里金插值中的变差函数，步骤中阴影衰落分量的空间相关性如式（31）所示。
87.关于基于残差克里金的电磁频谱地图构建装置的具体限定可以参见上文中对于
基于残差克里金法的电磁频谱地图构建方法的限定，在此不再赘述。上述基于残差克里金的电磁频谱地图构建装置中的各个模块可全部或部分通过软件、硬件及其组合来实现。上述各模块可以硬件形式内嵌于或独立于计算机设备中的处理器中，也可以以软件形式存储于计算机设备中的存储器中，以便于处理器调用执行以上各个模块对应的操作。
88.在一个实施例中，提供了一种计算机设备，该计算机设备可以是终端，其内部结构图可以如图6所示。该计算机设备包括通过系统总线连接的处理器、存储器、网络接口、显示屏和输入装置。其中，该计算机设备的处理器用于提供计算和控制能力。该计算机设备的存储器包括非易失性存储介质、内存储器。该非易失性存储介质存储有操作系统和计算机程序。该内存储器为非易失性存储介质中的操作系统和计算机程序的运行提供环境。该计算机设备的网络接口用于与外部的终端通过网络连接通信。该计算机程序被处理器执行时以实现一种基于残差克里金法的电磁频谱地图构建方法。该计算机设备的显示屏可以是液晶显示屏或者电子墨水显示屏，该计算机设备的输入装置可以是显示屏上覆盖的触摸层，也可以是计算机设备外壳上设置的按键、轨迹球或触控板，还可以是外接的键盘、触控板或鼠标等。
89.本领域技术人员可以理解，图6中示出的结构，仅仅是与本技术方案相关的部分结构的框图，并不构成对本技术方案所应用于其上的计算机设备的限定，具体的计算机设备可以包括比图中所示更多或更少的部件，或者组合某些部件，或者具有不同的部件布置。
90.在一个实施例中，提供了一种计算机设备，包括存储器和处理器，该存储器存储有计算机程序，该处理器执行计算机程序时实现上述任一方法实施例的步骤。
91.以上实施例的各技术特征可以进行任意的组合，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应当认为是本说明书记载的范围。
92.以上所述实施例仅表达了本技术的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本技术构思的前提下，还可以做出若干变形和改进，这些都属于本技术的保护范围。因此，本技术专利的保护范围应以所附权利要求为准。