卫星振动试验斜面上振动响应采集和转换方法及系统与流程

1.本发明涉及卫星正弦扫频振动试验数据采集和处理领域，具体地，涉及一种卫星振动试验斜面上振动响应采集和转换方法及系统。


背景技术：

2.正弦扫频振动试验(简称振动试验)卫星研制过程中要求进行的一项力学环境模拟试验，其目的是检验卫星在发射过程中经受低频振动环境并能正常工作的能力。试验过程中，需对星上关注部位的振动响应进行采集和处理，以掌握各部位的力学环境。在振动响应采集和处理时，通常要求星上布置的加速度传感器的测量轴与卫星坐标系各轴平行，以获得各部位在卫星坐标系下的振动响应。为实现此目的，对于星上斜面(即其法线不平行于卫星坐标系中任意一轴)，通常使用楔形块对传感器进行转接，以校正斜面与卫星坐标系的夹角，使得传感器的测量轴与卫星坐标系各轴平行。该方法需事先根据各斜面在卫星坐标系下的角度关系，加工相应角度的楔形块；在安装传感器时，先将楔形块安装在对应斜面上，再将传感器安装在楔形块上。无论是加工楔形块，还是转接安装传感器都费时、费力，这给斜面上振动响应采集和处理造成了一定的麻烦。
3.针对现有技术中的缺陷，本发明提供了一种经济、简单的卫星振动试验斜面上振动响应采集和转换方法。该方法直接在斜面上安装传感器而无需使用楔形块进行转接，并可以获得斜面在卫星坐标系下的振动响应，达到与使用楔形块转接后相同的效果。
4.对“数据采集和转换方法”进行检索，中国专利，专利申请号为cn201310624704.1。“一种智能变电站计量系统数据采集和转换方法”，该专利是一种智能变电站计量系统数据采集和转换方法，其特征在于，包括如下步骤：(1)按照设定规约类型实时采集一组待测数据；(2)设定t为缓存时间，缓存状态变化的待测数据，并在经过缓存时间t后，发送数据；(3)抽取所述步骤2)发送的数据中感兴趣的数据，更新存储到设定的数据库中，以供一个或多个其他规约类型的进程根据需要进行调用，与本专利

技术实现要素：
完全不同。中国专利，专利申请号为cn201710144300.0“一种实现虚拟验证系统数据采集的方法”，该专利是一种实现虚拟验证系统数据采集的方法，其特征在于，所述方法包括：s1、读取用户的操作，选择本次数据采集所针对的数据类型，是寄存器采集、变量采集还是内存数据采集；s2、针对本次的数据采集类型,读取用户的触发模式配置信息，判断是时间触发，还是地址触发；s3、根据已读取的数据采集类型以及数据采集触发形式，读取用户的数据采集信息，并生成专用命令字；s4、将生成的命令字通过特定命令管道传输至gdb模块；s5、gdb模块对命令字进行解析，封装成虚拟验证系统能够识别的专用数据结构；s6、通过虚拟验证系统的事件机制，将数据采集实例注入到系统当中；s7、完成一个数据采集实例的注入，与本专利发明内容完全不同。王盛智在论文“曲线图数据的快速采集与转换方法”(见《抚顺石油学院学报》2002年，200204期)中介绍利用扫描仪与autocad软件配合，在autocad环境下，通过编写autolisp程序来建立工程设计中的曲线图数据方法。解决了在使用计算机辅助工程设计时，如何将已有的经验或实验曲线图转换成计算机能够识别的数据文件问题。该论文中的数据采集与转
换方法与本发明完全不同。
5.目前，没有发现同本发明类似的说明或报告，也尚未收集到国内外类似的资料。
发明内容
6.针对现有技术中的缺陷，本发明的目的是提供一种卫星振动试验斜面上振动响应采集和转换方法及系统。
7.根据本发明提供的一种卫星振动试验斜面上振动响应采集和转换方法，包括：
8.步骤s1：获取星上需进行振动响应监测的斜面与卫星坐标系的角度关系；
9.步骤s2：在斜面上布置三向加速度传感器，根据斜面与卫星坐标系的角度关系得到测量坐标系轴的角度关系；
10.步骤s3：对卫星进行正弦扫频振动试验，传感器采集测量坐标系三个正交方向上的振动响应频谱；
11.步骤s4：对测量坐标系进行旋转形成新坐标系，并将在测量坐标系下获得的三向振动响应频谱转换至新坐标系下；
12.步骤s5：对旋转形成新坐标系进行第二次旋转，将第一次转换后的三向振动响应频谱转换至第二次转换后的坐标系下，得到转换至卫星坐标系下的三向振动响应频谱用于星上部件振动试验斜面上振动响应采集和转换处理。
13.优选地，在所述步骤s1中：
14.对于星上需进行振动响应监测的斜面，其法线与卫星坐标系存在夹角，不平行于卫星坐标系中任意一轴，通过实物测量或查阅设计方案，获得斜面的法线与卫星坐标系各轴的夹角；
15.记卫星坐标系为o
l
x
lylzl
，斜面的法线与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
16.在所述步骤s2中：
17.在该斜面上布置同时获取三个正交方向上的振动响应的加速度传感器，安装传感器时，不使用用于校正斜面与卫星坐标系的夹角的楔形块进行转接，使传感器的一个测量轴垂直于斜面，与斜面的法线平行，一个测量轴平行于卫星坐标系中任意两个轴形成的平面；
18.记传感器三个测量轴形成的坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；根据几何关系得到，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。
19.优选地，在所述步骤s3中：
20.对卫星进行正弦扫频振动试验，试验时利用传感器采集测量坐标系三个正交方向上的振动响应频谱，频谱表示为实部频谱和虚部频谱的形式，记在测量坐标系omxmymzm下x、y、z三个方向上的振动响应频谱分别为
[0021][0022][0023][0024]
式中，f为正弦扫描频率，i为虚数，为实部频谱，
虚部频谱；
[0025]
在测量坐标系omxmymzm下x、y、z三个方向上的幅值谱分别为
[0026][0027][0028][0029]
x、y、z三个方向上的相位谱分别为
[0030][0031][0032][0033]
优选地，在所述步骤s4中：
[0034]
将测量坐标系绕其轴中平行于卫星坐标系中两个轴形成的平面的轴旋转，使垂直于斜面的轴经旋转后平行于卫星坐标系轴，形成新坐标系；
[0035]
测量坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0036]
将坐标系omxmymzm绕omxm轴旋转γ角，使omzm轴经旋转后平行于o
lzl
轴，记旋转后形成的坐标系为omxmym′
zm′
，则omzm′
轴平行于o
lzl
轴；
[0037]
在新坐标系下，对在测量坐标系下获得的三向振动响应频谱进行转换处理，得到第一次转换后的三向振动响应频谱；其中，omxm向振动响应的幅值谱和相位谱不变，omym′
向振动响应的幅值谱和相位谱分别为：
[0038][0039][0040]
其中，a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；为y方向上的相位谱，φ
zm
为z方向上的相位谱；
[0041]
omzm′
向振动响应的幅值谱和相位谱分别为：
[0042][0043][0044]
为o
lzl
向振动响应的幅值谱和相位谱。
[0045]
优选地，在所述步骤s5中：
[0046]
将测量坐标系旋转形成的新坐标系绕其轴中平行于卫星坐标系轴的轴旋转，使其另两轴平行于卫星坐标系轴，从而形成新坐标系，将坐标系omxmym′
zm′
绕omzm′
轴旋转θ角，使omxm、omym′
轴经旋转后分别平行于o
l
x
l
、o
lyl
轴，记旋转后形成的坐标系为omxm″
ym″
zm′
，则坐标系omxm″
ym″
zm′
平行于卫星坐标系o
l
x
lylzl
；
[0047]
其中，转角θ满足：
[0048][0049][0050]
测量坐标系为omxmymzm，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0051]
在第二次转换的坐标系下，对第一次转换后的三向振动响应频谱进行转换处理，得到第一次转换后的的三向振动响应频谱，该频谱为转换至卫星坐标系下的三向振动响应频谱；
[0052]
其中，o
l
x
l
向振动响应的幅值谱和相位谱分别为：
[0053][0054][0055]
其中，a
xm
是测量坐标系omxmymzm下x方向上的幅值谱；为x方向上的相位谱，a
ym’为omym′
向振动响应的幅值谱，为omym′
向振动响应的相位谱；
[0056]olyl
向振动响应的幅值谱和相位谱分别为：
[0057][0058][0059]olzl
向振动响应的幅值谱和相位谱分别为
[0060][0061][0062]
其中，a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；为y方向上的相位谱，为z方向上的相位谱；
[0063]
为转换至卫星坐标系下的三向振动响应的幅值谱和相位谱。
[0064]
根据本发明提供的一种卫星振动试验斜面上振动响应采集和转换系统，包括：
[0065]
模块m1：获取星上需进行振动响应监测的斜面与卫星坐标系的角度关系；
[0066]
模块m2：在斜面上布置三向加速度传感器，根据斜面与卫星坐标系的角度关系得到测量坐标系轴的角度关系；
[0067]
模块m3：对卫星进行正弦扫频振动试验，传感器采集测量坐标系三个正交方向上
的振动响应频谱；
[0068]
模块m4：对测量坐标系进行旋转形成新坐标系，并将在测量坐标系下获得的三向振动响应频谱转换至新坐标系下；
[0069]
模块m5：对旋转形成新坐标系进行第二次旋转，将第一次转换后的三向振动响应频谱转换至第二次转换后的坐标系下，得到转换至卫星坐标系下的三向振动响应频谱用于星上部件振动试验斜面上振动响应采集和转换处理。
[0070]
优选地，在所述模块m1中：
[0071]
对于星上需进行振动响应监测的斜面，其法线与卫星坐标系存在夹角，不平行于卫星坐标系中任意一轴，通过实物测量或查阅设计方案，获得斜面的法线与卫星坐标系各轴的夹角；
[0072]
记卫星坐标系为o
l
x
lylzl
，斜面的法线与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0073]
在所述模块m2中：
[0074]
在该斜面上布置同时获取三个正交方向上的振动响应的加速度传感器，安装传感器时，不使用用于校正斜面与卫星坐标系的夹角的楔形块进行转接，使传感器的一个测量轴垂直于斜面，与斜面的法线平行，一个测量轴平行于卫星坐标系中任意两个轴形成的平面；
[0075]
记传感器三个测量轴形成的坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；根据几何关系得到，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。
[0076]
优选地，在所述模块m3中：
[0077]
对卫星进行正弦扫频振动试验，试验时利用传感器采集测量坐标系三个正交方向上的振动响应频谱，频谱表示为实部频谱和虚部频谱的形式，记在测量坐标系omxmymzm下x、y、z三个方向上的振动响应频谱分别为
[0078][0079][0080][0081]
式中，f为正弦扫描频率，i为虚数，为实部频谱，为实部频谱，虚部频谱；
[0082]
在测量坐标系omxmymzm下x、y、z三个方向上的幅值谱分别为
[0083][0084][0085][0086]
x、y、z三个方向上的相位谱分别为
[0087]
[0088][0089][0090]
优选地，在所述模块m4中：
[0091]
将测量坐标系绕其轴中平行于卫星坐标系中两个轴形成的平面的轴旋转，使垂直于斜面的轴经旋转后平行于卫星坐标系轴，形成新坐标系；
[0092]
测量坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0093]
将坐标系omxmymzm绕omxm轴旋转γ角，使omzm轴经旋转后平行于o
lzl
轴，记旋转后形成的坐标系为omxmym′
zm′
，则omzm′
轴平行于o
lzl
轴；
[0094]
在新坐标系下，对在测量坐标系下获得的三向振动响应频谱进行转换处理，得到第一次转换后的三向振动响应频谱；其中，omxm向振动响应的幅值谱和相位谱不变，omym′
向振动响应的幅值谱和相位谱分别为：
[0095][0096][0097]
其中，a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；为y方向上的相位谱，φ
zm
为z方向上的相位谱；
[0098]
omzm′
向振动响应的幅值谱和相位谱分别为：
[0099][0100][0101]
为o
lzl
向振动响应的幅值谱和相位谱。
[0102]
优选地，在所述模块m5中：
[0103]
将测量坐标系旋转形成的新坐标系绕其轴中平行于卫星坐标系轴的轴旋转，使其另两轴平行于卫星坐标系轴，从而形成新坐标系，将坐标系omxmym′
zm′
绕omzm′
轴旋转θ角，使omxm、omym′
轴经旋转后分别平行于o
l
x
l
、o
lyl
轴，记旋转后形成的坐标系为omxm″
ym″
zm′
，则坐标系omxm″
ym″
zm′
平行于卫星坐标系o
l
x
lylzl
；
[0104]
其中，转角θ满足：
[0105][0106][0107]
测量坐标系为omxmymzm，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0108]
在第二次转换的坐标系下，对第一次转换后的三向振动响应频谱进行转换处理，得到第一次转换后的的三向振动响应频谱，该频谱为转换至卫星坐标系下的三向振动响应频谱；
[0109]
其中，o
l
x
l
向振动响应的幅值谱和相位谱分别为：
[0110][0111][0112]
其中，a
xm
是测量坐标系omxmymzm下x方向上的幅值谱；为x方向上的相位谱，a
ym’为omym′
向振动响应的幅值谱，为omym′
向振动响应的相位谱；
[0113]olyl
向振动响应的幅值谱和相位谱分别为：
[0114][0115][0116]olzl
向振动响应的幅值谱和相位谱分别为
[0117][0118][0119]
其中，a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；为y方向上的相位谱，为z方向上的相位谱；
[0120]
为转换至卫星坐标系下的三向振动响应的幅值谱和相位谱。
[0121]
与现有技术相比，本发明具有如下的有益效果：
[0122]
1、本发明经济、简单，直接在斜面上安装传感器而无需使用楔形块进行转接，可以获得斜面在卫星坐标系下的振动响应，达到与使用楔形块转接后相同的效果；2、本发明可用于星上大部件振动试验斜面上振动响应采集和转换处理。
附图说明
[0123]
通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
[0124]
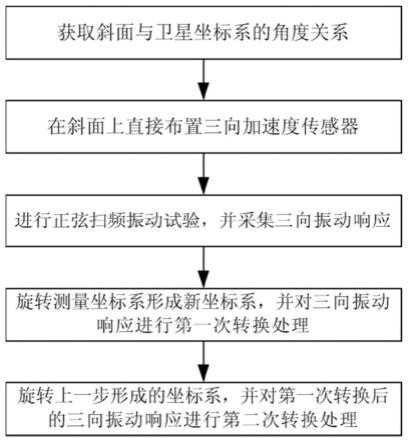
图1为本发明的步骤流程图；
[0125]
图2为传感器测量坐标系与卫星坐标系之间的关系；
[0126]
图3为三向振动响应时域信号从测量坐标系omxmymzm转换至坐标系omxmym′
zm′
的示意图；
[0127]
图4为转角θ与夹角α、β、γ之间的关系；
[0128]
图5为三向振动响应时域信号从坐标系omxmym′
zm′
转换至坐标系omxm″
ym″
zm′
(即坐标系o
l
x
lylzl
)的示意图。
具体实施方式
[0129]
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。
[0130]
实施例1：
[0131]
根据本发明提供的一种卫星振动试验斜面上振动响应采集和转换方法，如图1-图5所示，包括：
[0132]
步骤s1：获取星上需进行振动响应监测的斜面与卫星坐标系的角度关系；
[0133]
步骤s2：在斜面上布置三向加速度传感器，根据斜面与卫星坐标系的角度关系得到测量坐标系轴的角度关系；
[0134]
步骤s3：对卫星进行正弦扫频振动试验，传感器采集测量坐标系三个正交方向上的振动响应频谱；
[0135]
步骤s4：对测量坐标系进行旋转形成新坐标系，并将在测量坐标系下获得的三向振动响应频谱转换至新坐标系下；
[0136]
步骤s5：对旋转形成新坐标系进行第二次旋转，将第一次转换后的三向振动响应频谱转换至第二次转换后的坐标系下，得到转换至卫星坐标系下的三向振动响应频谱用于星上部件振动试验斜面上振动响应采集和转换处理。
[0137]
具体地，在所述步骤s1中：
[0138]
对于星上需进行振动响应监测的斜面，其法线与卫星坐标系存在夹角，不平行于卫星坐标系中任意一轴，通过实物测量或查阅设计方案，获得斜面的法线与卫星坐标系各轴的夹角；
[0139]
记卫星坐标系为o
l
x
lylzl
，斜面的法线与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0140]
在所述步骤s2中：
[0141]
在该斜面上布置同时获取三个正交方向上的振动响应的加速度传感器，安装传感器时，不使用用于校正斜面与卫星坐标系的夹角的楔形块进行转接，使传感器的一个测量轴垂直于斜面，与斜面的法线平行，一个测量轴平行于卫星坐标系中任意两个轴形成的平面；
[0142]
记传感器三个测量轴形成的坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；根据几何关系得到，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。
[0143]
具体地，在所述步骤s3中：
[0144]
对卫星进行正弦扫频振动试验，试验时利用传感器采集测量坐标系三个正交方向上的振动响应频谱，频谱表示为实部频谱和虚部频谱的形式，记在测量坐标系omxmymzm下x、y、z三个方向上的振动响应频谱分别为
[0145][0146][0147]
[0148]
式中，f为正弦扫描频率，i为虚数，为实部频谱，为实部频谱，虚部频谱；
[0149]
在测量坐标系omxmymzm下x、y、z三个方向上的幅值谱分别为
[0150][0151][0152][0153]
x、y、z三个方向上的相位谱分别为
[0154][0155][0156][0157]
具体地，在所述步骤s4中：
[0158]
将测量坐标系绕其轴中平行于卫星坐标系中两个轴形成的平面的轴旋转，使垂直于斜面的轴经旋转后平行于卫星坐标系轴，形成新坐标系；
[0159]
测量坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0160]
将坐标系omxmymzm绕omxm轴旋转γ角，使omzm轴经旋转后平行于o
lzl
轴，记旋转后形成的坐标系为omxmym′
zm′
，则omzm′
轴平行于o
lzl
轴；
[0161]
在新坐标系下，对在测量坐标系下获得的三向振动响应频谱进行转换处理，得到第一次转换后的三向振动响应频谱；其中，omxm向振动响应的幅值谱和相位谱不变，omym′
向振动响应的幅值谱和相位谱分别为：
[0162][0163][0164]
其中，a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；为y方向上的相位谱，φ
zm
为z方向上的相位谱；
[0165]
omzm′
向振动响应的幅值谱和相位谱分别为：
[0166][0167]
[0168]
为o
lzl
向振动响应的幅值谱和相位谱。
[0169]
具体地，在所述步骤s5中：
[0170]
将测量坐标系旋转形成的新坐标系绕其轴中平行于卫星坐标系轴的轴旋转，使其另两轴平行于卫星坐标系轴，从而形成新坐标系，将坐标系omxmym′
zm′
绕omzm′
轴旋转θ角，使omxm、omym′
轴经旋转后分别平行于o
l
x
l
、o
lyl
轴，记旋转后形成的坐标系为omxm″
ym″
zm′
，则坐标系omxm″
ym″
zm′
平行于卫星坐标系o
l
x
lylzl
；
[0171]
其中，转角θ满足：
[0172][0173][0174]
测量坐标系为omxmymzm，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0175]
在第二次转换的坐标系下，对第一次转换后的三向振动响应频谱进行转换处理，得到第一次转换后的的三向振动响应频谱，该频谱为转换至卫星坐标系下的三向振动响应频谱；
[0176]
其中，o
l
x
l
向振动响应的幅值谱和相位谱分别为：
[0177][0178][0179]
其中，a
xm
是测量坐标系omxmymzm下x方向上的幅值谱；为x方向上的相位谱，a
ym’为omym′
向振动响应的幅值谱，为omym′
向振动响应的相位谱；
[0180]olyl
向振动响应的幅值谱和相位谱分别为：
[0181][0182][0183]olzl
向振动响应的幅值谱和相位谱分别为
[0184][0185][0186]
其中，a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；为y方向上的相位谱，为z方向上的相位谱；
[0187]
为转换至卫星坐标系下的三向振动响应的幅值谱和相位谱。
[0188]
本发明也可用于星上大部件振动试验斜面上振动响应采集和转换处理。
[0189]
实施例2：
[0190]
实施例2为实施例1的优选例，以更为具体地对本发明进行说明。
[0191]
本领域技术人员可以将本发明提供的一种卫星振动试验斜面上振动响应采集和转换方法，理解为卫星振动试验斜面上振动响应采集和转换系统的具体实施方式，即所述卫星振动试验斜面上振动响应采集和转换系统可以通过执行所述卫星振动试验斜面上振动响应采集和转换方法的步骤流程予以实现。
[0192]
根据本发明提供的一种卫星振动试验斜面上振动响应采集和转换系统，包括：
[0193]
模块m1：获取星上需进行振动响应监测的斜面与卫星坐标系的角度关系；
[0194]
模块m2：在斜面上布置三向加速度传感器，根据斜面与卫星坐标系的角度关系得到测量坐标系轴的角度关系；
[0195]
模块m3：对卫星进行正弦扫频振动试验，传感器采集测量坐标系三个正交方向上的振动响应频谱；
[0196]
模块m4：对测量坐标系进行旋转形成新坐标系，并将在测量坐标系下获得的三向振动响应频谱转换至新坐标系下；
[0197]
模块m5：对旋转形成新坐标系进行第二次旋转，将第一次转换后的三向振动响应频谱转换至第二次转换后的坐标系下，得到转换至卫星坐标系下的三向振动响应频谱用于星上部件振动试验斜面上振动响应采集和转换处理。
[0198]
具体地，在所述模块m1中：
[0199]
对于星上需进行振动响应监测的斜面，其法线与卫星坐标系存在夹角，不平行于卫星坐标系中任意一轴，通过实物测量或查阅设计方案，获得斜面的法线与卫星坐标系各轴的夹角；
[0200]
记卫星坐标系为o
l
x
lylzl
，斜面的法线与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0201]
在所述模块m2中：
[0202]
在该斜面上布置同时获取三个正交方向上的振动响应的加速度传感器，安装传感器时，不使用用于校正斜面与卫星坐标系的夹角的楔形块进行转接，使传感器的一个测量轴垂直于斜面，与斜面的法线平行，一个测量轴平行于卫星坐标系中任意两个轴形成的平面；
[0203]
记传感器三个测量轴形成的坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；根据几何关系得到，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。
[0204]
具体地，在所述模块m3中：
[0205]
对卫星进行正弦扫频振动试验，试验时利用传感器采集测量坐标系三个正交方向上的振动响应频谱，频谱表示为实部频谱和虚部频谱的形式，记在测量坐标系omxmymzm下x、y、z三个方向上的振动响应频谱分别为
[0206][0207][0208][0209]
式中，f为正弦扫描频率，i为虚数，为实部频谱，为实部频谱，虚部频谱；
[0210]
在测量坐标系omxmymzm下x、y、z三个方向上的幅值谱分别为
[0211][0212][0213][0214]
x、y、z三个方向上的相位谱分别为
[0215][0216][0217][0218]
具体地，在所述模块m4中：
[0219]
将测量坐标系绕其轴中平行于卫星坐标系中两个轴形成的平面的轴旋转，使垂直于斜面的轴经旋转后平行于卫星坐标系轴，形成新坐标系；
[0220]
测量坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定；omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0221]
将坐标系omxmymzm绕omxm轴旋转γ角，使omzm轴经旋转后平行于o
lzl
轴，记旋转后形成的坐标系为omxmym′
zm′
，则omzm′
轴平行于o
lzl
轴；
[0222]
在新坐标系下，对在测量坐标系下获得的三向振动响应频谱进行转换处理，得到第一次转换后的三向振动响应频谱；其中，omxm向振动响应的幅值谱和相位谱不变，omym′
向振动响应的幅值谱和相位谱分别为：
[0223][0224][0225]
其中，a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；为y方向上的相位谱，φ
zm
为z方向上的相位谱；
[0226]
omzm′
向振动响应的幅值谱和相位谱分别为：
[0227][0228][0229]
为o
lzl
向振动响应的幅值谱和相位谱。
[0230]
具体地，在所述模块m5中：
[0231]
将测量坐标系旋转形成的新坐标系绕其轴中平行于卫星坐标系轴的轴旋转，使其另两轴平行于卫星坐标系轴，从而形成新坐标系，将坐标系omxmym′
zm′
绕omzm′
轴旋转θ角，使
omxm、omym′
轴经旋转后分别平行于o
l
x
l
、o
lyl
轴，记旋转后形成的坐标系为omxm″
ym″
zm′
，则坐标系omxm″
ym″
zm′
平行于卫星坐标系o
l
x
lylzl
；
[0232]
其中，转角θ满足：
[0233][0234][0235]
测量坐标系为omxmymzm，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ；
[0236]
在第二次转换的坐标系下，对第一次转换后的三向振动响应频谱进行转换处理，得到第一次转换后的的三向振动响应频谱，该频谱为转换至卫星坐标系下的三向振动响应频谱；
[0237]
其中，o
l
x
l
向振动响应的幅值谱和相位谱分别为：
[0238][0239][0240]
其中，a
xm
是测量坐标系omxmymzm下x方向上的幅值谱；为x方向上的相位谱，a
ym’为omym′
向振动响应的幅值谱，为omym′
向振动响应的相位谱；
[0241]olyl
向振动响应的幅值谱和相位谱分别为：
[0242][0243][0244]olzl
向振动响应的幅值谱和相位谱分别为
[0245][0246][0247]
其中，a
zm
是测量坐标系omxmymzm下z方向上的幅值谱；a
ym
是测量坐标系omxmymzm下y方向上的幅值谱；为y方向上的相位谱，为z方向上的相位谱；
[0248]
为转换至卫星坐标系下的三向振动响应的幅值谱和相位谱。
[0249]
实施例3：
[0250]
实施例3为实施例1的优选例，以更为具体地对本发明进行说明。
[0251]
本发明提供了一种卫星振动试验斜面上振动响应采集和转换方法。该方法通过获取斜面与卫星坐标系的角度关系、直接安装传感器、采集三向振动响应、实施转换处理等手段，从而获得斜面在卫星坐标系下的振动响应，达到与使用楔形块转接后相同的效果。该方法经济、简单，直接在斜面上安装传感器而无需使用楔形块进行转接。同时，本发明也可用于星上大部件振动试验斜面上振动响应采集和转换处理。
[0252]
在本实施例中，本发明提供的卫星振动试验斜面上振动响应采集和转换方法包括如下步骤：
[0253]
步骤1：对于星上需进行振动响应监测的斜面，其法线与卫星坐标系存在一定夹角(即不平行于卫星坐标系中任意一轴)，通过实物测量或查阅设计方案，获得斜面的法线与卫星坐标系各轴的夹角，即斜面与卫星坐标系的角度关系。记卫星坐标系为o
l
x
lylzl
，斜面的法线与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。
[0254]
步骤2：在该斜面上布置可同时获取三个正交方向上的振动响应的加速度传感器。安装传感器时，不使用用于校正斜面与卫星坐标系的夹角的楔形块进行转接，需使传感器的一个测量轴垂直于斜面(即与斜面的法线平行)，一个测量轴平行于卫星坐标系中任意两个轴形成的平面。记传感器三个测量轴形成的坐标系为omxmymzm，其中omzm轴垂直于斜面，omxm轴平行于o
l
x
lyl
平面，omym轴根据右手法则确定。根据几何关系可知，omzm轴与o
l
x
l
、o
lyl
、o
lzl
轴的夹角分别为α、β、γ。测量坐标系与卫星坐标系之间的关系见图2。
[0255]
步骤3：对卫星进行正弦扫频振动试验，试验时利用传感器采集测量坐标系三个正交方向上的振动响应频谱。该频谱一般表示为实部频谱和虚部频谱的形式，记在测量坐标系omxmymzm下三个方向上的振动响应频谱分别为
[0256][0257][0258][0259]
式中，f为正弦扫描频率，i为虚数，为实部频谱，为实部频谱，虚部频谱。则在测量坐标系omxmymzm下三个方向上的幅值谱分别为
[0260][0261][0262][0263]
三个方向上的相位谱分别为
[0264][0265][0266][0267]
步骤4：将测量坐标系绕其轴中平行于卫星坐标系中两个轴形成的平面的轴旋转，使垂直于斜面的轴经旋转后平行于卫星坐标系轴，从而形成新坐标系。即将测量坐标系omxmymzm绕omxm轴旋转γ角，使omzm轴经旋转后平行于o
lzl
轴。记旋转后形成的坐标系为omxmym′
zm′
，则omzm′
轴平行于o
lzl
轴。
[0268]
在新坐标系下，对在测量坐标系下获得的三向振动响应频谱进行转换处理，得到
第一次转换后的三向振动响应频谱。由于不能直接在频域中进行合成处理，需要转换至时域中进行相关推导。根据三向振动响应频谱可知，正弦扫描频率为f时对应的三向振动响应时域信号分别为
[0269][0270][0271][0272]
将三向振动响应时域信号从测量坐标系omxmymzm转换至坐标系omxmym′
zm′
的示意图见图3。在坐标系omxmym′
zm′
中，omxm向由于未旋转，因此其振动响应时域信号、频域幅值谱和相位谱不变。ym(t)、zm(t)在omym′
向的分量之和ym′
(t)为
[0273][0274]
式中，分别为omym′
向振动响应的幅值谱和相位谱，具体为
[0275][0276][0277]
同理，ym(t)、zm(t)在omzm′
向的分量之和zm′
(t)为
[0278][0279]
式中，分别为omzm′
向振动响应的幅值谱和相位谱，同时也是o
lzl
向振动响应的幅值谱和相位谱，具体为
[0280][0281][0282]
步骤5：将所述步骤4形成的坐标系绕其轴中平行于卫星坐标系轴的轴旋转，使其另两轴平行于卫星坐标系轴，从而又形成新坐标系。即将坐标系omxmym′
zm′
绕omzm′
轴旋转θ角，使omxm、omym′
轴经旋转后分别平行于o
l
x
l
、o
lyl
轴。记旋转后形成的坐标系为omxm″
ym″
zm′
，则坐标系omxm″
ym″
zm′
平行于卫星坐标系o
l
x
lylzl
。其中，转角θ与夹角α、β、γ之间的关系见图4。根据几何关系可知，
[0283][0284][0285]
在新坐标系下，对第一次转换后的三向振动响应频谱进行转换处理，得到第一次转换后的的三向振动响应频谱，该频谱即为最终转换至卫星坐标系下的三向振动响应频谱。将第一次转换后的三向振动响应时域信号从坐标系omxmym′
zm′
转换至坐标系omxm″
ym″
zm′
(即坐标系o
l
x
lylzl
)的示意图见图5。在坐标系o
l
x
lylzl
中，xm(t)、ym′
(t)在o
l
x
l
向的分量之和z
l
(t)为
[0286][0287]
式中，分别为o
lzl
向振动响应的幅值谱和相位谱，具体为
[0288][0289][0290]
xm(t)、ym′
(t)在o
lyl
向的分量之和y
l
(t)为
[0291][0292]
式中，分别为o
lyl
向振动响应的幅值谱和相位谱，具体为
[0293][0294][0295]
omzm′
向(即o
lzl
向)由于未旋转，因此其振动响应时域信号、频域幅值谱和相位谱不变，即o
lzl
向振动响应的幅值谱和相位谱分别为
[0296][0297][0298]
综上，即为最终转换至卫星坐标系下的三向振动响应的幅值谱和相位谱。
[0299]
本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统、装置及其各个模块以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统、装置及其各个模块以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同程序。所以，本发明提供的系统、装置及其各个模块可以被认为是一种硬件部件，而对其内包括的用于实现各种程序的模块也可以视为硬件部件内的结构；也可以将用于实现各种功能的模块视为既可以是实现方法的软件程序又可以是硬件部件内的结构。
[0300]
以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本技术的实施例和实施例中的特征可以任意相互组合。