一种基于BO-LSTM的锂离子电池剩余使用寿命预测方法

本发明属于水下航行器能源与动力应用研究，涉及一种基于bo-lstm的锂离子电池剩余使用寿命预测方法。

背景技术：

1、锂离子电池在动力能源领域被广泛应用，其使用过程中各性能参数的下降可能会造成电池失效、爆炸等不可挽回的损失。因此，对锂离子电池的剩余使用寿命进行预测是必要的。

2、目前预测方法普遍以间接特征参数为基础，在预测rul过程中会累计误差。本文以电池剩余循环次数(remaining useful life，rul)与电池健康状态(state of health，soh)之间的关系为基础，通过构建贝叶斯—长短期记忆(bayesian long and short-termmemory,bo-lstm)神经网络算法，预测电池剩余循环次数，只需一次预测过程即可预测电池rul，提高了预测精度。

技术实现思路

1、要解决的技术问题

2、为了避免现有技术的不足之处，本发明提出一种基于bo-lstm的锂离子电池剩余使用寿命预测方法，解决水下航行器动力系统中电池剩余循环次数预测不准确的问题，为电池得剩余循环次数预测提供参考。

3、技术方案

4、一种步骤1：对电池进行充放电循环试验，得到电池的失效后总循环次数，并将总循环次数划分为训练集与测试集；

5、所述训练集数目为总循环次数的前80％或前90％；

6、所述测试集数目为总循环次数减去训练集数目；

7、步骤2：计算电池健康度：

8、

9、其中，c0为初始测得的放电容量；ci为第i次实时测得的放电容量；

10、步骤3：将电池健康度数据代入bo-lstm算法模型，对电池剩余使用寿命进行预测：

11、步骤3.1：将步骤2的电池健康度作为bo-lstm神经网络模型的初始输入样本，随机产生初始化样本；

12、步骤3.2：将初始化的样本点输入进行高斯运算，得到目标函数的均值和方差：

13、步骤3.3：将目标函数的均值和方差输入到ei采集函数中，采样函数输出修正后的高斯模型中选取下一组需要评估的样本点xi；

14、该样本评估点输入lstm模型中进行训练，获得目标函数新的输出值yi，以输出值yi更新样本集合即电池健康度的集合d＝{(x1,y1),(x2,y2),(xt,yt)}和高斯模型；

15、步骤3.4：重复迭代，在迭代设定次数内，以每次输出值yi更新样本集合d＝{(x1,y1),(x2,y2),…(xt,yt)}和高斯模型；

16、当迭代完成终止，采样函数输出最佳的电池健康度的集合参数以及对应的lstm模型的目标函数的损失值(xi,yi)；

17、电池健康度的集合d＝{(x1,y1),(x2,y2),(xt,yt)}中个数的1/2为电池的循环预测寿命。

18、所述对电池进行充放电循环试验的过程为：设置电池的失效阈值，在室温状态下对电池进行充放电循环试验，得到电池失效的总循环次数。

19、所述电池的失效阈值为电池初始容量的80％。

20、所述以步骤3样本集合dt与步骤1获得的充放电循环试验中的电池总循环次数进行对比，验证模型算法精度。

21、所述bo-lstm算法模型：通过乘法门即输入门it、遗忘门ft和输出门ot，将存储单元连接而成的；lstm算法进行前向传播和反向传播，前向推算采用激活函数，反向推算使用反向传播算法进行梯度计算，在以下计算过程中wij表示神经元i到j之间的权值，表示t时刻神经元j的激活函数，表示t时刻lstm算法网络输入到神经元j的值。下标i、φ、w和c分别表示输入门、遗忘门、输出门和c的一个记忆单元，f表示三个乘法门的激活函数，g和h分别表示神经元的输入激活函数和输出激活函数，表示t时刻记忆单元c的状态，记忆模块与记忆模块之间的相互连接是由神经元自身的输出实现的，而记忆模块中三个乘法门的激活函数只在其内部起作用，lstm神经网络算法包括如下步骤：

22、步骤1)：输入序列为x，时间长度为t，lstm算法的前向推算以t＝1开始递增，直至，随着时间的推移，前向推算的方程也在相应的递推更新；而反向推算是以t＝t为起始点，并不断的递减，直至t＝1；根据rnn算法的后向推算公式，最终的权值t＝t导数值表示为：

23、

24、其中，当t＝0和t＝t+1时，网络中所有的表达式和激活函数都设置为0；

25、步骤2)：lstm算法的前向推算方程如下：

26、输入门it在t时刻的表达式：

27、

28、遗忘门ft在t时刻的表达式：

29、

30、记忆单元在t时刻的表达式：

31、

32、输出门ot在t时刻的表达式：

33、

34、步骤3)：lstm算法的反向推算方程，设

35、记忆单元在t时刻的输出值为：

36、输出门ot在t时刻的表达式：

37、t时刻的状态：

38、记忆单元的权值导数值为：

39、遗忘门ft的权值导数值为：

40、输入门it的权值导数值为：

41、所述步骤3.2～步骤3.4的高斯运算过程：建立贝叶斯全局优化算法：

42、

43、其中，f表示未知的目标函数；d表示已观测到的参数和观测值集合d＝{(x1,y1),(x2,y2),…(xt,yt)}；xt表示观测到的数据；yt表示观测值；p(f|d)表示f的后验概率；p(d|f)表示y的似然分布；p(f)表示的f的前验概率；p(d)表示的f的边际似然分布；

44、所述观测值就是电池每一次充放电循环测得的电池的容量值。

45、所述贝叶斯算法包括概率代理模型和采样函数两个核心过程,概率代理模型是用来代理未知目标函数的概率模型，通过信息量的迭代增加，不断的对先验概率进行修正，从而使得代理模型更加准确；采样函数根据后验分布，通过在最可能出现全局最优解的区域和还未取样的区域进行采样，从候选集中选择一个最有“潜力”的样本点，使得损失函数值最小,具体包括如下步骤：

46、步骤(1)：高斯过程由一个均值函数μ(x)和一个半正定的协方差函数k(x,x')构成，高斯分布表示成如下形式：

47、f(x)～gp(μ(x),k(x,x'))

48、其中，μ(x)表示f(x)的数学期望，通常均值函数设置为0；f(x)表示平均绝对误差；k(x,x')表示x的协方差函数；

49、步骤(2)：探索过的历史信息为d1:t＝{x1:t,f1:t}，其中ft＝f(xt)，所要搜寻的下一个值为xt+1，协方差矩阵k记为下式：

50、

51、步骤(3)：ft和ft+1都服从联合高斯分布，其均值为0，其联合高斯分布表示为下式：

52、

53、其中，

54、步骤(4)：求边缘密度函数，得到ft+1的后验概率：

55、

56、其中，均值μt(xt+1)和方差计算公式分别如下：

57、μt(xt+1)＝ktk-1f1:t

58、

59、估计出xt+1在任意取值处服从的正态分布，从而使用采样函数去定位下一个最优的样本点；

60、步骤(5)：对f(x)的均值和方差抽样进行样本计算，抽样的ei采集函数为：

61、

62、其中，φ(·)为标准正态分布的概率密度函数，φ(·)为标准正态分布的分布函数，式中z表示为：

63、

64、步骤(6)：ei算法加入权衡标量ξ且满足ξ＞0的ei采集函数如下：

65、

66、

67、有益效果

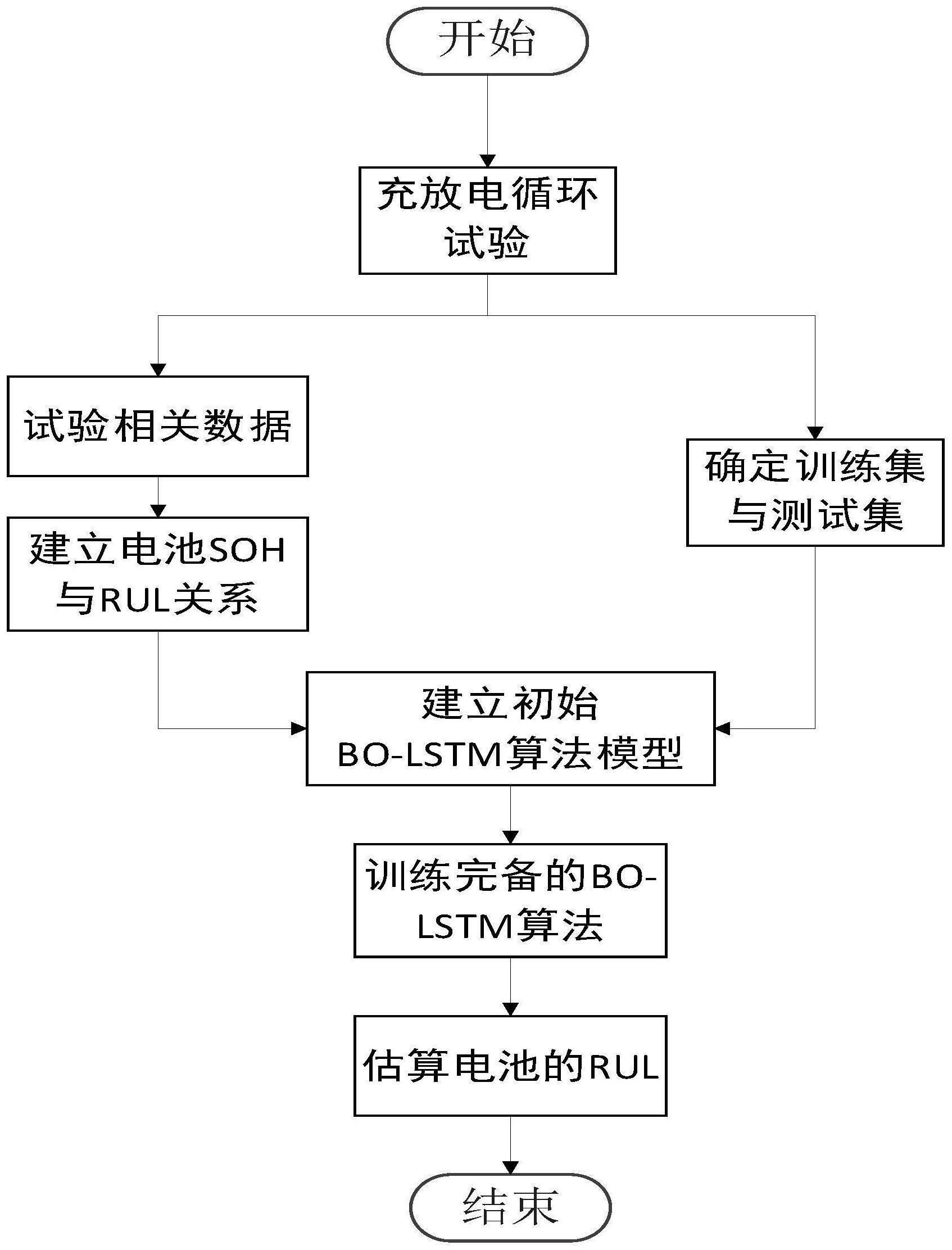
68、本发明提出的一种基于bo-lstm的锂离子电池剩余使用寿命预测方法，旨在解决水下航行器动力系统中电池剩余循环次数预测不准确的问题，为电池的剩余循环次数预测提供参考。其特征为：1.对电池进行充放电循环试验并划分训练集与测试集2.建立电池健康度与剩余使用寿命的联系；3.建立bo-lstm模型；4.将数据代入bo-lstm算法模型，对电池剩余使用寿命进行预测。本发明方法将lstm神经网络算法良好的拟合能力与贝叶斯优化算法优秀的寻优能力结合，为锂离子电池剩余使用寿命的预测提供了一种更高精度的方法，从而能够更准确的对锂离子电池剩余使用寿命进行预测。