一种水下机器人重浮心量化配平方法与流程

本发明涉及水下机器人结构设计，特别涉及一种水下机器人重浮心量化配平方法。

背景技术：

1、为了保证水下机器人稳定运行，应保有一定的稳心高度。为此，工程师在水下机器人结构设计过程中，会制定详细的重浮心计算表，借助三维设计软件的测量，初步得到水下机器人的重浮心位置。进一步，在水下机器人水池配平过程中，基于设计参数，再将水下机器人吊放入水中，通过简单力矩平衡计算和反复试错的方法，确定最终配重铅块或者浮力块的质量和位置参数，使水下机器人浮心在重心的上方。配平后水下机器人在水中处于零纵倾角，换言之水下机器人上平面与水面保持平行。配平后水下机器人浮力状态处于一般为零浮力或者微正浮力状态。

2、由于水下机器人结构设计阶段，不可能完全将所有的线缆、管路以及其它柔性体的细节表现在设计图纸里，而这些细节所占的重浮力比重又不可忽略，会造成设计计算得到的重浮心参数与实物存在较大误差。若以设计参数为基础确定配重参数，则会增加零纵倾角配平过程中的试错次数。上述操作方式，仅能够满足部分对重浮心位置要求不严格水下机器人的基础配平需求，对于配置成稳心高为零等高要求的场景就无能为力。

3、因此对重浮心要求严格的水下机器人配平需要更加精细化的测算试验方法。现有对水下机器人进行精细化测算配平的方法为：水下机器人装配完成后，重新单独测量每一个水密零部件、透水零部件、以及线缆、水密接插件等的质量，并逐一吊入水后测量其浮力质量，然后将这些参数赋值到三维设计软件对应的每个零部件上，再经软件内部求解得到水下机器人整体的质心和浮心；进而经过力矩平衡计算，得到配重参数，再经实际水池配平调整后完成水下机器人的量化配平，以实现水下机器人的零稳心高配平。

4、但是该方法的缺点是需要将装配好的水下机器人重新按部件拆开单独称重，由于水下机器人的部件数量众多、拆卸及起吊操作的步骤繁琐，因此容易导致最终理论与实际的水下机器人重浮心不可避免地存在较大误差。

技术实现思路

1、本发明的目的是提供一种水下机器人重浮心量化配平方法，本方案全程均采用单点悬吊，相比现有常规的双吊点或者多点称重测量方法，本方案不需额外的测量设备，实验条件更简单，测算过程亦相对简单，本方案的测算及配平成本低，操作简单，适用范围广，能对绝大多数的水下机器人进行测量，且不受水下机器人质量分布的影响。

2、本发明的上述技术目的是通过以下技术方案得以实现的：

3、一种水下机器人重浮心量化配平方法，包括：

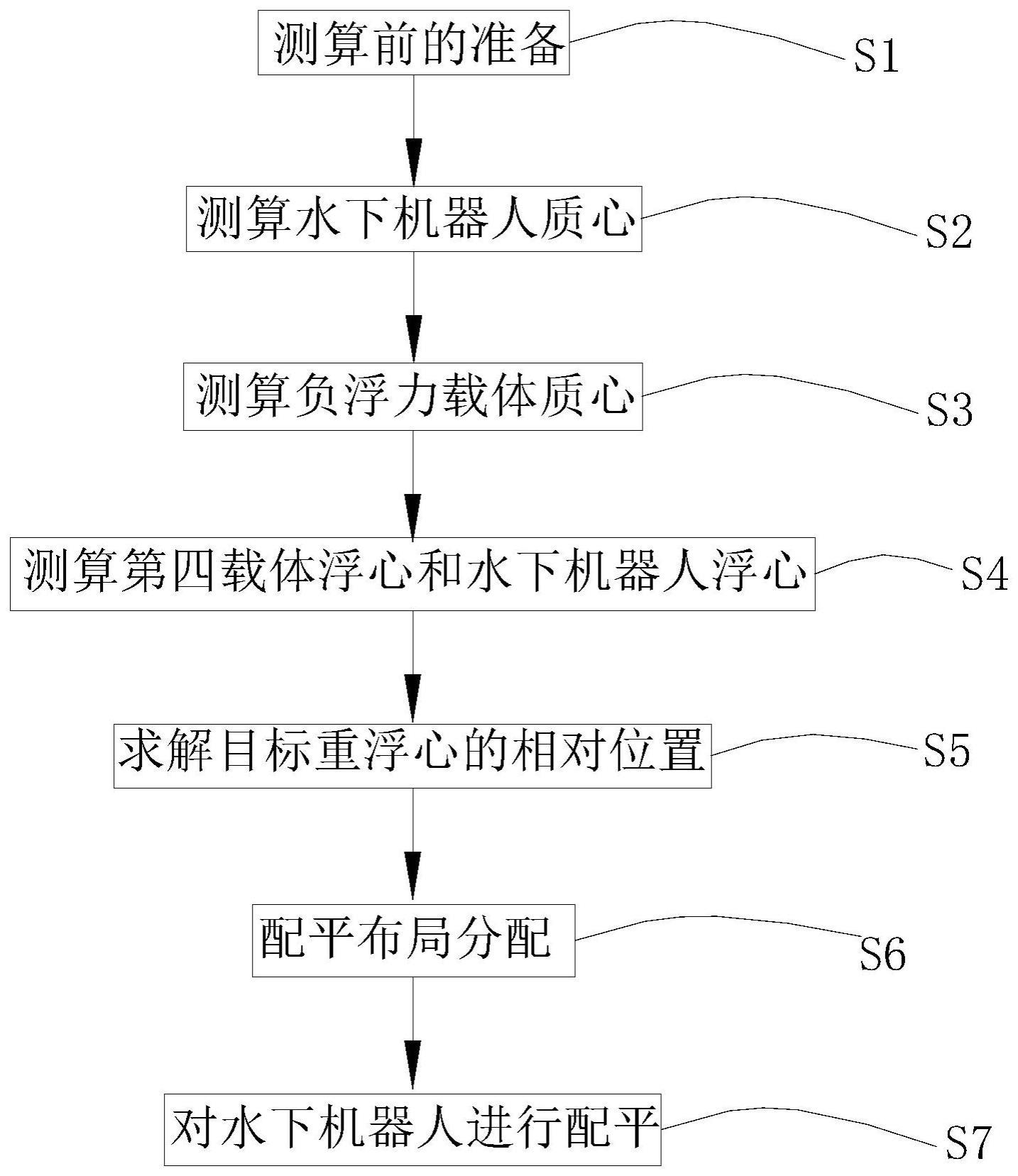
4、测算前的准备：

5、于水下机器人上建立位置坐标系，确定水下机器人吊点位置a；

6、测算水下机器人质心：

7、为水下机器人配置第一配重块以组成第一载体，通过计算获得水下机器人重心、第一载体重心；

8、测算负浮力载体质心：

9、将水下机器人配置成负浮力载体，将负浮力载体通过吊点位置a悬吊于大气环境中，为负浮力载体配置第二配重块以组成第二载体，通过计算获得第二载体重心、第二配重块重心；

10、为第二载体配置第三配重块以组成第三载体，通过计算获得第三载体重心；

11、测算第四载体浮心和水下机器人浮心：

12、将第四载体吊放沉没于水中，为第二载体配置第四配重块以组成第四载体，通过计算获得第四载体浮心，根据第四载体浮心计算后获得水下机器人的浮心位置；

13、求解目标重浮心的相对位置：

14、根据水下机器人的重力、负浮力载体的浮力以及水下机器人的浮心、最终配重块的水中质量，通过计算后获得最终等效配重的配平位置；

15、对水下机器人进行配平：

16、根据配平位置，将最终配重块配置于水下机器人。

17、由此，相对于现有技术中需要多个吊点进行水下机器人悬吊的方案，本方案能通过简单的单点悬吊(吊点位置a)测算步骤，以实现水下机器人上配平位置的计算，最后将最终配重块准确地配置于配平位置上，进而实现水下机器人配平后达到目标重浮心相对位置的要求(比如稳心高、重浮心重合、浮心在中心上方5mm前方2mm等类似的要求)；本方案的配平过程清晰明了，配平及测算操作过程简洁，配平测算要求的实验条件简单，能够避免传统繁琐重复的经验试错式配平，由此可见，本方案是一种低成本高效配平方案。

18、而且由于本方案全程均采用单点悬吊，因此只需要一个吊钩配合吊秤来对水下机器人上的单个吊点进行称重即可，相比现有常规的双吊点或者多点称重测量方法，本方案不需额外的测量设备，即不需要特定的测量仪器，只通过少量简单的测量工具便可进行测算，实验条件更简单，测算过程亦相对简单。综上所述，本方案的测算及配平成本低，操作简单，适用范围广，能对绝大多数的水下机器人进行测量，且不受水下机器人质量分布的影响。

19、在一些具体实施方式中，在测算水下机器人质心的步骤中，将水下机器人通过吊点位置a悬吊于大气环境中，此时采集水下机器人的质量为m，水下机器人的纵倾角θ1；当为水下机器人配置第一配重块以组成第一载体后，采集第一配重块的质量为mq1，第一载体的纵倾角θ2；

20、设水下机器人重心g＝[xg,zg]，第一载体重心ga1＝[xga1,zga1]，

21、公式(1)：其中第一载体的质量ma1＝m+mq1；

22、公式(2)：

23、联立公式(1)、(2)，可计算获得水下机器人重心g＝[xg,zg]、第一载体重心ga1＝[xga1,zga1]。

24、由此，本方案提供了一种根据单吊点的测算方法，以用于计算水下机器人重心以及配重有第一配重块后的第一载体重心。

25、在一些具体实施方式中，

26、于所述测算水下机器人质心的步骤中，将水下机器人配置成负浮力载体，将负浮力载体通过吊点位置a悬吊于大气环境中，采集负浮力载体的倾角θ2，第二配重块的为mq2，第二载体的质量为ma2，第二载体的纵倾角为θ3；

27、设第二载体重心ga2＝[xga2,zga2]，第二配重块重心gq2＝[xgq2,zgq2]，

28、公式(3)：其中第二载体的质量ma2＝m+mq2；

29、设第三载体的重心ga3＝[xga3,zga3]，

30、公式(4)：其中第三载体的质量ma3＝m+mq2+mq3；

31、第三配重块的质量为mq3，第三载体的纵倾角为θ3；

32、公式(5)：

33、联立公式(3)-(5)后可计算获得第二载体重心ga2＝[xga2,zga2]，第二配重块重心gq2＝[xgq2,zgq2]，第三载体的重心ga3＝[xga3,zga3]。

34、由此，本方案提供了一种基于单吊点进行水下机器人质心测算的具体操作及测算步骤，其具有操作简单的特点。

35、在一些具体实施方式中，于所述测算负浮力载体质心的步骤中，将第二配重块、水下机器人分别吊放沉没于水中，此时采集水下机器人的浮力质量mb、第二配重块的水中质量mq2w，水下机器人与第二配重块与第二载体满足公式(6)：m>mb-mq2w时，第二配重块浮心等于第二配重块重心，即bq2＝[xbq2,zbq2]＝gq2＝[xgq2,zgq2]。

36、由此，本方案通过利用水下机器人分别在大气中所采集的质量数据以及水中时所采集的质量数据两者与第二配重块在水中时所采集的质量数据的关系，以简单地推算出第二配重块浮心等于第二配重块重心的特点，以便于进一步简化测算流程。

37、在一些具体实施方式中，于所述测算第四载体浮心和水下机器人浮心的步骤中，将第二载体吊放沉没于水中，采集此时第二载体的水中质量ma2w和纵倾角θw1；第四配重块的质量为mq4，采集第四载体的纵倾角θw2，

38、公式(7)：

39、ma2((xga1-xa)cosθw1-(zga1-za)sinθw1)-ma2b((xba1-xa)cosθw1-(zba1-za)sinθw1)＝0，其中第二载体浮力质量ma2b＝ma2-ma2w；

40、设第四载体重心ga4＝[xga4,zga4]，公式(8)：其中第四载体质量ma4＝ma2+mq4；

41、设定第四载体浮心ba2＝[xba4,zba4]，公式(9)：其中第四载体质量ma4b＝ma2b+mq4b，第四配重块浮力质量mq4b＝mq4-mq4w；

42、公式(10)：

43、ma4((xga4-xa)cosθw2-(zga4-za)sinθw2)-ma4b((xba4-xa)cosθw2-(zba4-za)sinθw2)＝0；

44、联立公式(7)至公式(10)后，计算获得第四载体浮心ba2＝[xba2,zba2]；

45、公式(11)：

46、将第四载体浮心ba2＝[xba2,zba2]代入公式(11)后，计算获得水下机器人的浮心b＝[xb,zb]。

47、由此，本方案提供了一种基于单吊点的水下机器人浮心测算方式，其具有操作简单的特点。

48、在一些具体实施方式中，于所述求解目标重浮心的相对位置的步骤中，根据最终配重块沉没于水中的称重为mqw、水下机器人的浮力质量mb、最终配重块的浮力mqb＝mq-mqw，重复所述测算水下机器人质心的步骤，计算获得最终配重块与水下机器人组合后的重心g0＝[xg0,zg0]以及浮心b0＝[xb0,zb0]；

49、设定最终配重块的最终期望重浮心相对位置egb＝[xegb,zegb]，最终配重块的配平位置gq＝[xgq,zgq]、浮心位置bq＝[xbq,zbq]；

50、公式(12)：

51、根据最终配重块与水下机器人组合后的重心g0＝[xg0,zg0]以及浮心b0＝[xb0,zb0]，进一步求解公式(12)，计算获得最终配重块的配平位置gq。

52、由此，本方案提供了一种计算获得最终配重块配平位置的具体测算方式。

53、在一些具体实施方式中，所述最终配重块被构造为实心，使最终配重块的配平位置gq等于浮心位置bq。

54、由此，通过对最终配重块的限定，以便于进一步简化测算的步骤。

55、在一些具体实施方式中，在所述求解目标重浮心的相对位置与对水下机器人进行配平的步骤之间还设有配平布局分配步骤，所述配平布局分配步骤：

56、在水下机器人上预设有若干个等效配重位置px，每个等效配重位置px上配置有质量为mpx的等效配重块，其中等效配重块满足公式(13)，

57、其中公式(13)：

58、由此，考虑到在实际配平过程中，由于最终配重块的体积过大时，在配平位置无法进行配重固定，则需要进行配重布局分配，在本方案中，等效配重位置px中的x为若干个，具体地，本方案的数量为四个，分别为p1-p4，在坐标系中的位置坐标描述分别对应为[xp1,zp1]、[xp2,zp2]、[xp3,zp3]、[xp4,zp4]；由此可见，每个等效配重位置px满足等效配重位置的选择即可，可以根据水下机器人的零部件布局作为基础，在水下机器人结构设计时预留空间，使得最终配重块能够灵活地将零部件间隙作为配重区域。

59、在一些具体实施方式中，于所述配平布局分配步骤中还包括微正浮力配平，在最终配重块与水下机器人组合后的重心g0处配置浮力块，使水下机器人配置成微正浮力载体。

60、由此，本方案提供了一种能够使水下机器人配置成正浮力状态的具体实施方式。

61、在一些具体实施方式中，于所述配平布局分配步骤中，当所述配平位置超出水下机器人的最大高度尺寸时，在最终配重块与水下机器人组合后的重心g0在x轴的两侧分别配置浮力材料、等效配重块。

62、由此，本方案考虑到如果最终配重后的水下机器人稳心高的要求较小时，可能会出现配平位置超出水下机器人最大高度尺寸的情况，本方案提供了一种能够解决这种情况的技术方案，以此来最大限度地减少目标稳心高的问题。

63、综上所述，本方案全程均采用单点悬吊，相比现有常规的双吊点或者多点称重测量方法，本方案不需额外的测量设备，实验条件更简单，测算过程亦相对简单，本方案的测算及配平成本低，操作简单，适用范围广，能对绝大多数的水下机器人进行测量，且不受水下机器人质量分布的影响。