一种被动声纳目标距离及运动轨迹估计方法与流程

本发明涉及水声探测，尤其涉及一种被动声纳目标距离及运动轨迹估计方法。

背景技术：

1、被动声纳目标方位、距离、运动参数及其运动航迹是非常重要的目标信息要素，是目标态势估计、威胁估计和指挥决策的重要依据，也是水声信号与信息处理的重要研究内容。

2、被动声纳主要有两种部署方式：一是安装在固定位置的静止平台，如海底固定阵；二是安装在移动平台，如潜艇或水面舰船；而安装在运动平台的被动声纳是当前和未来最主要的形式。由于被动声纳只能估计目标方位，无法给出目标距离，因此大大限制了其实际使用效率。由此，被动声纳目标距离估计也成为水声信号处理领域的主要课题。

3、目前，被动目标距离估计的主要方法包括：一是基于海洋环境先验信息的匹配场方法，它需要掌握比较精确的海洋水声环境信息，计算量比较大；二是三子阵的测距方法，其精度与子阵间距和目标距离有关，一般适用于目标距离较近的情况；三是基于浅海波导不变量的距离估计法，利用目标运动在lofar谱产生的干涉条纹，通过获取条纹的斜率估计目标距离，这种方法主要适用于浅海、且目标距离较近的情况。对于运动平台的被动声纳，目标运动分析(tma)方法是解决运动目标距离和运动参数估计的经典方法，它是一种纯方位目标运动参数估计方法，利用被动声纳平台运动中观测到的目标方位时序信息，建立量测方程和目标运动状态方程，基于最小二乘、卡尔曼滤波、不敏滤波等技术，进行目标位置和运动参数估计，该方法要求声纳平台是运动的，而且目标状态必须是可观测的。但对于声纳平台和目标平台都是匀速直线运动的情况，tma方法建立的目标状态是不可观测的，为了改善可观测性，在目标运动参数解算过程中，声纳平台至少需要做一次转向机动。在实际应用中，这种方法主要存在声纳平台需要机动、计算时间长(一般对于水中目标需要10-30分钟)，算法容易发散、甚至无解等问题，严重影响实际应用效果。

4、基于多普勒频移特性的目标定位在雷达、无线电通信、无线电侦察等领域有着广泛的应用，现有的方法都是以一定观测时间内的多普勒频移量进行定位或速度估计的。因为雷达观测目标(尤其是空中目标)的速度快，雷达和无线电通信的频率非常高，多普勒频移现象非常明显、一定观测时间内的多普勒频移量比较大，因此在雷达、通信侦察等领域的应用比较成功。然而，水下目标(尤其是水下安静运动的目标)运动速度慢，被动声纳工作的频率低，这种背景下信号在一定时间内的多普勒频移量非常小，因此，基于常规多普勒频移特性的目标速度估计或定位方法不稳定、收敛解算时间长(甚至难以收敛)，无法满足水声目标定位要求。

5、目前，对于静止不动的水声系统，利用多普勒频移进行被动目标距离估计的方法主要包括：一是基于单水听器多普勒频移信息的距离估计，这种方法只能在目标运动到最近接收点为目标函数等方法，试图求解目标运动参数的闭式解，这类模型复杂、计算过程复杂，计算时间长，而且需要较准确是解算初始值，否则难以收敛。二是一种基于静止被动声纳多普勒的目标距离及轨迹估计方法，利用被动声纳提取的目标方位和线谱信息，通过对多普勒频移通用公式的变换推导，基于运动三角形，提出一套针对匀速直线运动目标进行距离和运动参数估计的直接而简明的计算模型，只需三个观测时刻的目标方位和线谱频率信息，即可实现静止被动声纳的目标距离、航向航速和运动轨迹估计，该方法无需迭代运算，计算速度快，目标方位变化率和线谱频率变化率越大、效果越好。然而，该方法仅适用于静止平台的声纳，不适用于运动平台的声纳。

6、对于运动平台的被动声纳，目标与声纳平台的运动态势相对静止声纳更加复杂，不可控的因素大大增加，被动目标距离和运动要素的求解更加困难，也是当前面临的难题。

技术实现思路

1、本发明针对现有运动平台进行被动目标运动参数和距离估计的不足，提供一种被动声纳目标距离及运动轨迹估计方法，通过挖掘声纳平台和目标平台运动的特殊几何关系，推导建立了一套用于运动平台被动声纳的目标航向航速、距离及其运动轨迹估计的解析模型。利用一定时间间隔的三个时刻目标方位和线谱频率观测，实现被动目标的距离、航向航速和运动轨迹估计。在声纳平台静止时，仍然适用，通用性强。进一步，针对平台运动和声传播时延导致的距离估计误差提出了修正方法。并通过连续观察和动态计算，得到类似于主动声纳的目标运动航迹图，可为被动目标跟踪、识别和指挥决策提供更加丰富而重要的目标指示信息。本技术发明适用于声纳平台与目标平台不在同一连线上运动情况下、各种运动态势的被动目标定位，也可应用于雷达、电子侦察和无线电领域。

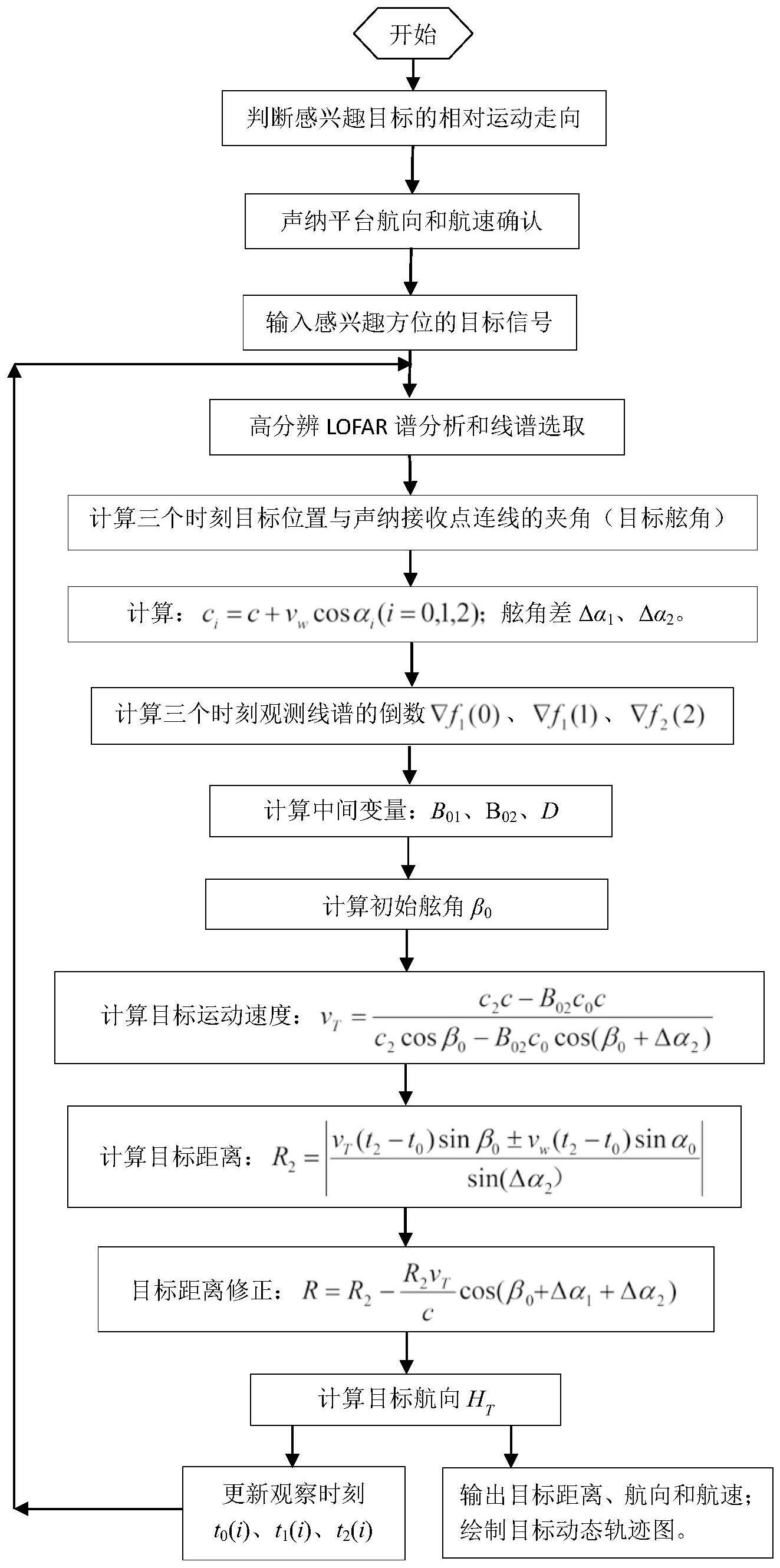
2、本发明提供了一种被动声纳目标距离及运动轨迹估计方法，包括：

3、通过声纳平台一次转向判别法判断目标相对声纳平台运动走向，并确认解算目标位置和运动参数过程中声纳平台的航向和航速；

4、对所述目标信号进行高频率分辨率的谱分析；

5、计算三个时刻所述目标位置与声纳接收点连线的夹角，所述夹角即目标舷角；

6、建立基于运动平台声纳的目标辐射噪声信号线谱多普勒频移模型；建立声纳平台相对目标平台舷角与所述目标舷角之间的关系式；

7、根据目标方位和多普勒频移信息及所述关系式估计初始舷角和目标运动速度；根据所述初始舷角和目标运动速度估计目标距离和运动航向，并进行距离修正；

8、根据所述目标运动速度、目标距离及运动航向通过连续观测法得到完整的目标距离、运动航向和速度估计序列，并动态绘制目标轨迹。

9、进一步地，所述通过声纳平台一次转向判别法判断目标相对声纳平台运动走向，包括：设定目标真方位为ψwf，则将声纳平台航向变为hwz＝ψwf，即将声纳平台朝着发现目标的方位线运动；当声纳平台到达航向hwz＝ψwf后，通过短时间观察目标相当于声纳平台舷角的变化，根据以下方式判别所述目标相对声纳平台运动走向：当声纳平台是向右转向目标方位线，即原始航向hw<ψwf时：如果目标舷角α向左舷变化，则目标运动走向与声纳平台航向hw同向运动，否则反向；当声纳平台是向左转向目标方位线，即原始航向hw>ψwf时：如果目标舷角向右舷变化，则目标运动走向与声纳平台原航向hw同向运动，否则反向。

10、进一步地，所述确认解算目标位置和运动参数过程中声纳平台的航向和航速，包括：确认声纳平台保持匀速直线运动，且选择新的航向。

11、进一步地，采用zoomfft、长时长数据的fft、mvdr高分辨谱估计、短时长补零的fft方法中的任意一种对所述目标信号进行高频率分辨率的谱分析；假如目标信号包含多根线谱，则选择线谱信号强、相对稳定而且工作频段内频率更高的线谱。

12、进一步地，所述计算三个时刻所述目标位置与声纳接收点连线的夹角，包括：在t0、t1、t2时刻声纳平台分别位于w0、w1、w2点，三个时刻声纳检测到目标分别位于t0、t1、t2位置点辐射的信号，观测到的目标的真方位分别为ψw0、ψw1、ψw2，推算得到三个时刻声纳平台相对于目标平台的真方位分别为ψt0、ψt1、ψt2；真方位和航向的取值范围均为0°-360°；

13、t0、t1、t2三个观测时刻目标位于声纳平台的舷角分别为：

14、α0＝|ψw0-hw|                            (1-1)

15、α1＝|ψw1-hw|                            (1-2)

16、α2＝|ψw2-hw|                            (1-3)

17、定义α0、α1、α2为0°-180°范围的正值。

18、进一步地，所述建立基于运动平台声纳的目标辐射噪声信号线谱多普勒频移模型，包括：设在t0、t1、t2三个观测时刻声纳平台位于目标平台的舷角分别为β0、β1、β2，检测并选择到目标辐射噪声信号的某根线谱频率分别为：f1(0)、f1(1)、f1(2)，根据相对运动态势可以表示为：

19、

20、

21、

22、令：

23、c0＝c+vwcosα0，c1＝c+vwcosα1，c2＝c+vwcosα2         (5)

24、因为α0、α1、α2为三个观测时刻得到的目标舷角，且声纳平台速度vw已知，因此c0、c1、c2为可观测的已知量。

25、进一步地，所述建立声纳平台相对目标平台舷角与所述目标舷角之间的关系式，包括：

26、当目标平台与声纳平台同向而行时：

27、β1＝β0+△α1，△α1＝|α0-α1|                  (6-1)

28、β2＝β0+△α2，△α2＝|α0-α2|                  (6-2)

29、当目标平台与声纳平台反向而行时：

30、β1＝β0-△α1，△α1＝|α0-α1|                    (6-1')

31、β2＝β0-△α2，△α2＝|α0-α2|                  (6-2')。

32、进一步地，所述根据目标方位和多普勒频移信息及所述关系式估计初始舷角和目标运动速度，包括：将(5)式代入(2)、(3)、(4)式，然后再将(2)式分别除以(3)、(4)式，并记：

33、

34、

35、由(7-1)式可得：

36、

37、由(7-2)式可得：

38、

39、合并(8-1)和(8-2)式，：

40、

41、令则(9)式变为：

42、

43、再将角度关系式(6)代入(10)式，整理(10)式便可得初始舷角β0的求解公式：

44、

45、由(8-1)、(8-2)式分别实现目标速度估计：

46、

47、

48、进一步地，所述根据所述初始舷角和目标运动速度估计目标距离和运动航向，并进行距离修正，包括：

49、目标距离根据声纳平台运动三角形和目标运动三角形估计得到：

50、当声纳平台与目标平台同向而行时，t2时刻目标距离r2为：

51、

52、当声纳平台与目标平台反向而行时，则t2时刻目标距离r2为：

53、

54、考虑传播时延，经修正得到观测时刻的真实距离r可近似表示为：

55、

56、目标运动航向估计方法为：

57、首先计算t0时刻声纳平台相对于目标的真方位：

58、

59、再根据运动态势和β0，可得到目标的运动航向：

60、

61、进一步地，所述根据所述目标运动速度、目标距离及运动航向通过连续观测法得到完整的目标距离、运动航向和速度估计序列，包括：

62、通过以下(1)或(2)的方法得到所述完整的目标距离、运动航向和速度估计序列；

63、(1)以第一次运动参数估计的t0时刻为基准，以一定观测时间间隔δt，得到第i次参数估计的三个观测时刻:

64、

65、按照t0(i)、t1(i)、t2(i)时刻的目标方位和线谱频率观测量进行连续估计；

66、(2)前两个观测时刻和目标方位及其线谱频率的观测值不变，仅改变第3个观测量的获取时刻t2进行连续观察估计，即：

67、

68、通过本发明提供的一种被动声纳目标距离及运动轨迹估计方法，能够实现以下有益效果：

69、1、本发明专利利用被动声纳可观测的目标方位，以及基于目标方位信号lofar谱分析得到的线谱频率，通过分析和挖掘声纳平台和目标平台运动的特殊几何关系，重新推导建立了一套适用于所有被动声纳目标航向航速、距离及其运动轨迹估计的简洁模型。进一步，针对平台运动和声传播时延导致的距离估计误差提出了距离修正方法。在此基础上，提出了一套解决被动声纳目标定位和运动轨迹估计的完整方案。本发明在声纳平台速度为零时，退化为静止声纳平台的情况，同样可以求解目标航向航速及其距离等参数。因此本发明专利的适用范围更广，在声纳平台不运动的情况下仍然可用。

70、2、本发明通过分析运动平台之间的角度关系，挖掘了未知舷角变量β1、β2与未知舷角β0、已知观测量α0、α1、α2之间的关系式，将5个未知量转化3个独立的未知量，由此便可利用三个时刻的观测方程，求解得到目标运动参数vt、和初始舷角β0，使得原本不可求解的目标运动参数估计问题变得可实现，而且极大简化了目标距离和运动参数估计的算法模型。

71、3、本发明基于运动几何原理，提出了一种适用于各种相对运动态势的目标距离估计解析模型，无需迭代运算，利用目标航速和初始舷角估计值，可快速、稳定求解第3个观测时刻的目标距离；进一步，为解决海洋声传播时延造成的距离误差，提出了一种距离修正方法。

72、4、本发明将目标观测的真方位差值作为系统的输入数，由此得到目标运动观测过程中的目标舷角差(即舷角变化量)作为解算的模型参数，这样可以消除目标方位(舷角)观测的系统误差，从而提高目标距离和运动参数估计精度。

73、5、本发明提出了目标运动走向判别的有效方法，为实现基于目标方位和线谱频率进行被动目标运动参数和距离估计奠定了重要基础。

74、6、本发明提出了解算目标位置和运动参数过程中声纳平台的航向和航速的确认原则，以及高分辨lofar谱分析的基本方法，有助于提高目标运动参数估计的效率和精度。

75、7、本发明提出了基于连续观察三个时刻目标方位和频率信息的目标运动轨迹(方位、距离)和航速航向动态估计方法，可以按一定时间间隔动态估计得到第1次目标参数估计以后的目标轨迹和运动参数，得到连续观测时刻的方位、距离、速度航向，继而绘制出运动目标的极坐标或直角坐标的动态轨迹图。本技术发明可以得到类似于雷达(主动声纳)的探测效果，而且数据刷新率不受发射重复周期限制，具有秒级的数据刷新率，极大丰富了被动目标指示信息，具有非常独特的技术优势。

76、8、本发明提出了一套被动声纳目标运动参数、距离和轨迹估计装置，提供了基于三个观测时刻的目标方位和单线谱频率就可估计目标运动参数、距离和运动轨迹的完整解决方案。适用于声纳平台运动或静止的被动目标运动参数、距离和轨迹估计。目标运动的方位变化率、多普勒频率变化率越大，目标定位、运动参数和轨迹估计的效果越好。