一种双转子系统动平衡的方法

本发明涉及航空发动机领域，是一种以定转速比下的转子模态替代实际工作转速线下的转子模态进行双转子系统n1+n2平面模态动平衡的方法。

背景技术：

1、现代航空发动机在追求高性能时，同时引起发动机转子系统向着转速越来越高，结构越来越“柔”的方向发展。目前国内外航空发动机转子结构都以双转子系统为主，并且多数航空发动机都具有中介轴承，结构复杂，动力学耦合强，加之，工作环境恶劣，振动问题一直都是发动机研制中的“瓶颈”。统计结果表明，航空发动机中约60％的振动超标问题是由转子不平衡所引起的。发动机在组装前都会对高、低压转子的各个旋转部件分别进行较高精度的动平衡。组装成整机后，在高转速、高负荷和高温下工作，双转子系统的平衡精度很容易遭到破坏。再者，发动机工作转速范围内，双转子系统存在若干阶模态，转子振动对转子不平衡及其变化很敏感。另外，对于未来高性能发动机，“可容模态”是其重要的性能指标，发动机要在若干阶模态下“容忍共振”，转子系统的振动将会对不平衡更加敏感。而在发动机使用过程中，转子不平衡状态会时常变化，需要频繁进行转子动平衡，但对于双转子系统，其具有低压转子激励和高压转子激励的两组振动模态，且两组振动模态的正交性受转速比影响，常规的动平衡方法中，忽略了双转子系统的模态正交性，导致平衡的各阶模态之间相互影响，为此本文提出了以定转速比下的转子模态替代实际工作转速线下的转子模态进行双转子系统n1+n2平面模态动平衡的方法。

2、seve f在“balancing of machinery with a flexible variable-speed rotor[j]”，《journal of sound and vibration》,2003,204:287-302中在转子动力学理论的基础上结合有限元法与影响系数平衡法，编写了用于柔性转子的数值计算方法，然而对于双转子系统，由于中介轴承与陀螺效应的影响，导致双转子系统在影响系数法进行动平衡时，在未知模态下的影响系数并不能保持恒定，因此需要提出一种可以对中介轴承的耦合效应解耦，影响系数恒定且平衡时不影响其他阶模态的动平衡方法。

3、黄江博在“航空发动机双转子系统模态正交性和不平衡响应[j]”，《振动与冲击》，2022,41(21):176-189一文中针对带中介轴承的双转子系统高压激励模态与低压激励模态的正交性进行了分析，采用复模态的方法推导了双转子系统模态正交性的条件集合，发现当双转子系统的速比不变时，双转子系统在各自激励方式下的模态关于刚度矩阵与惯量矩阵是正交的，但在不同激励方式下的模态之间不存在正交性，其次采用模态正交性对双转子系统的不平衡响应进行了模态分解，发现低压转子上的不平衡量只会激起低压转子主激励下的模态振动；高压转子上的不平衡量只会激起高压转子主激励下的模态振动，本发明则是基于上述的研究结论，确定了满足双转子系统模态正交性的条件，即发动机高压转子与低压转子转速比值在平衡过程中始终保持定值，在平衡时按照高压激励的模态在高压转子上进行动平衡，低压激励的模态在低压转子上进行动平衡，保证了平衡高压转子时所添加的配重不影响低压转子且对高压激励的其他阶模态不产生影响，平衡低压时依然遵循此规律。

4、王四季在“航空发动机柔性转子动平衡方法[j]”,《噪声与振动控制》，2011,06：91-94+115,(doi：10.3969/j.issn.1006-1355-2011.06.020)一文中，根据航空发动机的特点，结合影响系数法与模态动平衡方法，建立了向前和向后的柔性转子混合平衡方法，然而这种方法只能对单转子系统进行动平衡，这中方法虽然能有效的对转子系统进行动平衡，降低发动机的启停次数以及添加试重个数，但对于复杂的双转子系统结构，其存在多源激励与耦合振动的问题，上述方法无法进行实施。

5、现有的航空发动机双转子系统模态判断和表达方式存在的上述不足，制约了双转子系统模态特性的研究。

技术实现思路

1、为了克服现有技术中存在平衡转速范围内某一阶模态时而影响其他阶模态，模态振型受转速比影响而无法满足正交性条件，双转子系统高压转子与低压转子耦合效应问题，本发明提出了一种双转子系统动平衡的方法。

2、本发明的具体过程是：

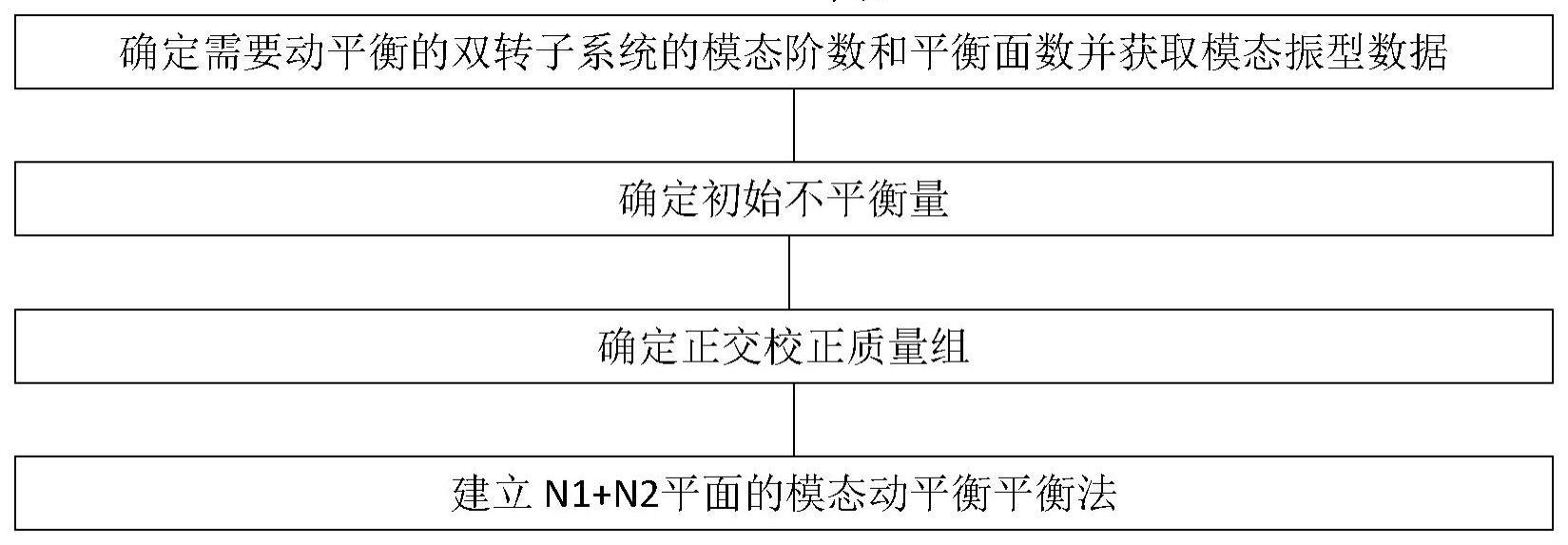
3、步骤1，确定需要动平衡的双转子系统的模态阶数和平衡面数，并获取模态振型数据。

4、当所述模态阶数中低压转子激励为主激励时，为低压转子激励模态阶数，其中需要进行动平衡的低压转子激励模态阶数的数量为nl2；当所述高压转子激励为主激励时，为高压转子激励模态阶数，其中需要进行动平衡的高压转子激励模态阶数的数量为nh1。

5、所述模态阶数为四阶模态，分别为高压激励第一阶模态、第二阶模态与低压激励第一阶模态、第二阶模态。

6、确定的平衡面数中：在高压转子上的平衡面数的数量n1；该高压转子平衡面数的数量n1与高压转子激励模态阶数的数量nh1相同；在低压转子上的平衡面数的数量为n2，该低压转子平衡面数的数量n2与低压转子激励模态阶数的数量nl2相同。

7、所确定的平衡面数为四个，分别为高压一级压气机盘x1、高压涡轮盘x2、低压风扇盘x3和低压涡轮盘x4。

8、获取的模态振型数据中，第k阶高压转子激励模态振型数据为rhk；第i阶低压转子激励模态振型数据为rli。为方便后续步骤计算，将各阶模态振型数据整合为矩阵形式。其中高压转子为主激励的模态振型数据rhk整合为模态数据矩阵rh；低压转子为主激励的模态振型数据rli整合为模态数据矩阵rl。所述高压转子主激励的模态数据矩阵rh的行数和低压转子主激励的模态数据矩阵rl的行数均与需要动平衡的模态阶数一致；所述高压转子主激励的模态数据矩阵rh的列数与选取的高压转子平衡面数n1一致；所述低压转子主激励模态数据矩阵rl的列数与选取的和低压转子平衡面数n2一致。第k阶高压转子激励模态数据rhk如公式(3)所示，其中各参数表示第rhk阶模态在各平衡面处的模态振型数据：

9、rhk＝[rhkh1 rhkh2 … rhkn1]t，hk＝1,2,...,nh1                   (3)

10、第i阶低压转子激励模态数据rli如公式(4)所示，其中各参数表示第rli阶模态在各平衡面处的模态振型数据：

11、rli＝[rlil1 rlil2 … rlin2]t，li＝1,2,...,nl2                   (4)

12、得到的四个平衡面处的各阶模态振型数据。

13、各阶模态在平衡面处的幅值与相对应的相位弧度数值如表1所示，表中相位为弧度，幅值为无量纲数值

14、表1双转子实验器模态动平衡所用振型数据

15、

16、

17、步骤2，确定初始不平衡量：

18、ⅰ确定所述双转子系统在低压转子激励下的第li阶模态不平量

19、当双转子系统的低压转子转速接近低压转子激励第li阶临界转速ωli时，不平衡响应r(x,t)为：

20、

21、式(5)中，rli(x)为低压激励的第li阶模态振型数据，为由现有技术得到的关于转速ωli的频响函数，为第li阶模态不平衡量。

22、根据不平衡响应与不平衡量两者的影响系数计算转子系统第li阶模态不平衡量具体过程如下：

23、在低压转子转速为ωli，且高压转子转速为ωhk时，测量双转子系统的振动：测量时，当不加试重组时，初始不平衡量记为u0，双转子系统的不平衡响应记为r0；当添加试重组为u1后，测量到该转子系统的不平衡响应为r1。则下述关系式成立：

24、r1-r0＝rli(x)fli(ωli)u1                          (7)

25、由于不加试重组时双转子系统的不平衡响应为r0＝rli(x)fli(ωli)u0,带入式(7)则初始不平衡量为：

26、

27、式中，u0为第li阶模态不平衡量

28、ⅱ确定所述双转子系统在高压转子激励下的第hk阶模态不平量

29、当双转子系统的高压转子转速接近高压转子激励第hk阶临界转速ωhk时，高压转子转速ωhk＝ωhk，定转速比数值为a，低压转子转速

30、按照上述确定第li阶模态不平量相同的方法确定所述双转子系统在高压转子激励下的第hk阶模态不平量

31、步骤3，确定正交校正质量组：

32、所述校正质量组分布t与平衡的模态振型相似，且与其余阶模态振型保持正交。

33、对于平衡的低压激励的第li阶模态，设校正质量组为tli的行向量，对于所有低压转子激励下的nl2阶振型，有n2个正交校正质量组，其中n2＝nl2。该n2个正交校正质量组则可由下列方程组求得：

34、

35、对于平衡的高压激励的第hk阶模态，设校正质量组为thk的行向量，对于所有高压转子激励下的nh1阶模态振型，有n1个正交校正质量组，其中n1＝nh1。该n1个正交校正质量组通过下列方程组求得：

36、

37、步骤4，建立n1+n2平面的模态动平衡平衡法：

38、所述建立n1+n2平面的模态动平衡平衡法中，对于平衡高压转子激励的第hk阶模态不平衡量，平衡的高压激励的模态阶数为nh1阶，通过步骤1选取高压转子系统上的平衡面数为n1，通过步骤3获取的正交校正质量为thk；配重为为n1个平衡校正面上加的配重。步骤2中确定的模态不平衡量使配重满足如下关系：

39、

40、式中，rhk(xhk)thk＝-1，故：

41、

42、双转子第hk阶模态为高压转子激励下的模态，在高压转子校正面上施加配重就能平衡转子第hk阶模态不平衡。由于选择的thk仅满足rhk(xhk)thk＝-1，故：

43、

44、因此，所加的高压转子平衡配重会影响其余高压转子激励的模态不平衡，即双转子高压激励的第hk+1阶模态不平衡状态会受到影响。配重的激励频率为高压转子转速，所以该配重不会影响低压转子激励下的模态不平衡。完成第hk阶高压激励模态的平衡，该过程便是平衡高压转子激励下的第hk阶高压激励模态的方法。

45、在平衡完第hk阶高压激励模态后，继续平衡高压转子激励下的第hk+1阶模态。在进行高压转子激励下的第hk+1阶模态平衡时，需要在高压转子上选用n1个平衡面施加配重为使添加的配重不对第hk阶模态平衡结果产生影响，thk+1需满足以下条件：

46、

47、此时，配重为而此时的不仅含有初始不平衡量的影响，还含有高压转子激励hk阶模态不平衡校正量的影响。按照式(14)确定的比例关系，将配重以各平衡面分量的形式分别添加各个平衡面上。

48、完成第hk+1阶高压激励模态的平衡，该过程便是平衡高压转子激励下的第hk+1阶高压激励模态的方法。

49、平衡低压转子激励的各阶模态不平衡量的方法与所述平衡高压转子激励下的第hk阶和第hk+1阶高压激励模态的方法类似。

50、所述航空发动机双转子系统包含了高压转子两个平衡面与低压转子两个平衡面，工作转速内共出现了高压激励的两阶模态与低压激励的两阶模态，需要平衡的模态为高压激励第一阶模态、第二阶模态与低压激励第一阶模态、第二阶模态。

51、ⅰ平衡高压转子激励下的第一阶模态。

52、双转子系统中，平衡高压激励一阶模态时的正交试重组为高压压气机0度试重，高压涡轮盘180度试重。按照上述过程获取的正交配重组为高压压气机盘150度高压涡轮盘10度。

53、ⅱ平衡高压转子激励下的第二阶模态和低压转子激励下的第一阶模态

54、如果在高压激励下的第二阶模态不平衡未校正之前，转子继续升速，能达到低压激励下的第一阶临界转速。同时平衡高压转子激励下的第二阶模态和低压转子激励下的第一阶模态。按照所述平衡高压转子激励下的第hk阶和第hk+1阶高压激励模态的方法，得到高压激励的二阶模态的正交配重组和低压激励的一阶模态的正交配重组。在高压转子平衡面与低压转子平衡面上按照分量形式添加高压激励的二阶模态的正交配重组和低压激励的一阶模态的正交配重组。

55、如果在高压激励下的第二阶模态不平衡未校正之前，由于振动超标，转子不能继续升速到低压激励下的第一阶临界转速，则先平衡高压激励下的第二阶模态，再平衡低压激励下的第一阶模态。按照所述平衡高压转子激励下的第hk+1阶模态的方法平衡高压转子激励下的第二阶模态。按照所述平衡高压转子激励下的第一阶模态的过程平

56、在双转子系统中，平衡低压激励一阶模态时正交试重组为低压风扇盘180度，低压涡轮盘0度试重，获取的正交配重组为低压涡轮盘110度试重，风扇盘不添加。

57、ⅲ平衡低压转子激励下的第二阶模态

58、按照平衡高压转子激励下的第二阶模态的类似的方法平衡低压转子激励下的第二阶模态。在低压转子激励下的二阶临界转速状态下，测量转子的初始运行振动响应和加试重之后的振动响应，按照所述平衡高压转子激励下的第hk+1阶高压激励模态的方法，得到低压转子激励下的第二阶模态不平衡校正质量，并按照各平衡面分量的形式分别添加各个平衡面上。

59、至此，完成了双转子系统n1+n2平面模态动平衡。

60、与现有技术相比较，本发明取得的有益效果为：

61、本发明所提出的航空发动机双转子系统针对现有技术中存在双转子航空发动机平衡某一阶模态时影响到其他阶模态，发动机启停次数多，平衡时高低压转子耦合效果难以消除等主要问题：

62、1、本发明系统性地建立了航空发动机双转子系统n1+n2平面的模态动平衡方法，通过数学关系式，明确的对航空发动机双转子系统在高压为主激励时的模态下与低压转子为主激励时的模态下的正交校正质量组进行了计算，平衡的定转速比条件可在发动机双转子系统在实际运行时采用双参数输入法可进行控制。

63、2、在进行动平衡时，将高压激励的模态与低压激励的模态分开平衡，并添加试重与配重时，高压转子激励模态添加试重只需选取高压转子的平衡面，低压转子同理，可以有效的避免高压转子之间的平衡效果相互干扰，避免了高、低压转子之间的耦合效应，因现有技术中已提出高压转子上的不平衡量分布只会影响高压转子激励的模态振动，低压转子上的不平衡分布，只会影响低压转子激励的模态振动。

64、3、在航空发动机双转子系统模态动平衡时，采用影响系数法与模态动平衡法相结合的形式对双转子系统各个平衡面的试重组与配重组进行计算，综合了模态动平衡不影响其他阶次的模态振动以及影响系数法算法简单等优点，使动平衡效果更明显。

65、解决以上关键问题后，将本发明的方法应用于航空发动机双转子系统的动平衡，对双转子航空发动机的振动超标具有控制与抑制作用，为航空发动机安全运行提供了可靠和有效的保证。在图2中选取高压涡轮盘处的不平衡响应进行对比，减振比可达72.4％，图3中选取低压涡轮盘处的不平衡响应进行对比，减振比可达41.4％，能够看出来该方法对转子航空发动机的振动超标有明显的控制与抑制作用。