一种最小均方宽度约束的高斯束形态优化方法与流程

本发明属于地震偏移成像，具体涉及一种最小均方宽度约束的高斯束形态优化方法。

背景技术：

1、随着我国勘探开发难度逐步增大，勘探目标开始向裂缝油气藏、岩性油气藏等复杂构造探区转移，复杂起伏地表也逐渐常态化，近地表和中深层速度的横向骤变使得地震数据的处理过程更加棘手，研究高精度、适应性强的叠前深度偏移算法在后续的地震解释、属性分析及储层预测中具有重要意义。

2、工业界常用的几种深度域成像方法分别是逆时偏移、傅立叶有限差分偏移、克其霍夫偏移和高斯束偏移。上述四种方法各有利弊：基于波动方程双程精确解的逆时偏移是发展至今成像精度最高的偏移方法，但该方法计算效率较低、消耗内存大；傅立叶有限差分偏移既可作用于时间域，也可作用于频率域，但其成像精度无法与逆时偏移相提并论；克其霍夫偏移由于其具备的独一无二的计算效率优势、对非规则观测数据的匹配能力，正广泛应用于商业化规模生产，但在地球物理勘探中无法处理复杂构造成像问题，并不能满足目标区块的精细勘探要求。高斯束偏移方法不仅能解决克其霍夫偏移的理论缺陷(焦散区振幅奇异、阴影区无波场能量和多次波至问题等)，沿袭其灵活性、高效性，且对复杂高陡构造、断块区域具有与波动方程类偏移不相上下的成像适应性；此外，其对初始深度域速度场的依赖性弱于波动方程类偏移方法，常规的走时层析方法获取的速度模型即可满足成像要求。

3、公开号为cn111210495a的中国发明专利申请公开了一种三维模型驱动方法、装置、终端及计算机可读存储介质，其方法包括：确定三维模型的目标骨骼，目标骨骼从至少两个候选骨骼中得到；将目标骨骼与三维模型绑定，其中，目标骨骼用于驱动三维模型运动。公开号为cn110138426a的中国发明专利申请公开了一种基于卫星通信的全景波束构建方法、系统、设备和介质，其应用于地面站，其方法包括：模拟卫星调制的历史下行数据；对模拟卫星调制的下行数据进行解调，得到设定数量航天器对应的解调参数；获取卫星调制的实时下行数据，基于解调参数对实时调制的下行数据进行解调，得到实时调制的下行数据中携带的设定数量航天器的信号特性数据。其通过仿真实际场景获得地面站设备所需要的解调参数，并基于获取的解调参数改进相应的地面站设备，基于改进后的地面站设备能够实现了静态全景波束的布设，使得与地面站设备通信的通信卫星能够覆盖其覆盖范围内的所有航天器，实现了与地面站通信的用户中心与每一个航天器的实时通讯。

4、在现有技术中，传统高斯束偏移方法通常在频率域实现，其中最为典型是hill和gray等提出的炮域高斯束偏移算法；此后，该算法被逐渐拓展到真振幅、起伏地表、各向异性介质、以及诸多新型地震波束偏移方法，如控制束、快速束、聚焦束、菲涅尔束、复值束、自适应聚焦束等。高斯束偏移虽然克服了克其霍夫偏移不能处理多波至和单程波波动方程偏移不能对陡倾构造准确成像的缺点，但在陆地勘探这种复杂地表、复杂构造的双复杂条件下，其成像精度取决于所选择的初始波束宽度，即：当初始波束宽度较小时，近地表成像精度较高，但此时中深层成像质量较差；反之当初始波束宽度较大时，中深层成像质量提高，但近地表成像精度降低。因而，为获取更为理想的偏移成果剖面，即：在保证中深层成像质量的同时，也要兼顾近地表的成像精度，需要一种新型高斯波束形态优化方法。

技术实现思路

1、本发明的目的是提供一种最小均方宽度约束的高斯束形态优化方法，以解决高斯束偏移方法近地表和中深层的成像精度矛盾，使得偏移成果剖面更加准确可靠，有利于后续解释处理。

2、为了实现以上目的，本发明所采用的技术方案是：

3、一种最小均方宽度约束的高斯束形态优化方法，包括以下步骤：

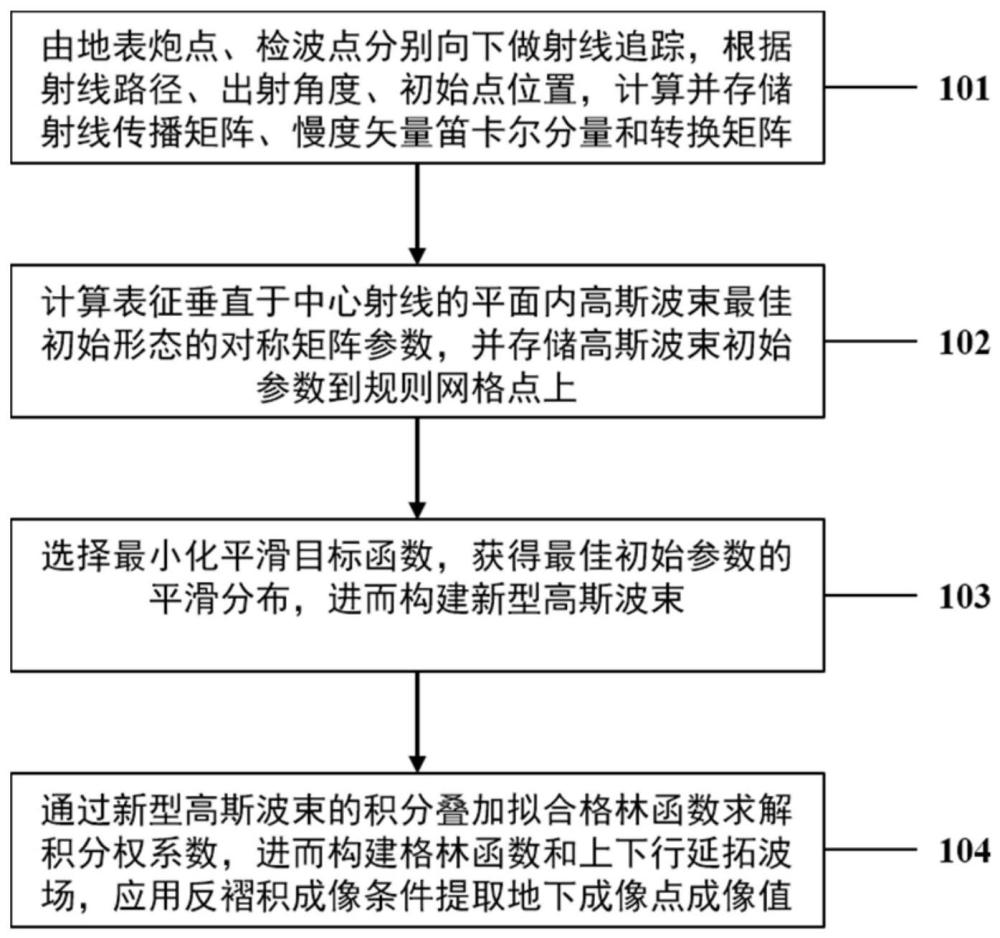
4、(1)根据射线路径、出射角、初始点位置，计算并存储射线传播矩阵、慢度矢量笛卡尔分量和转换矩阵；

5、(2)计算表征垂直于中心射线的平面内高斯波束最佳初始形态的对称矩阵参数，并存储高斯波束初始参数到规则网格点上；

6、(3)选择最小化初始参数表征的平滑目标函数，获得初始参数的平滑分布，进而构建新型高斯波束；

7、(4)通过新型高斯波束的积分叠加拟合解析格林函数求解积分权系数，进而构建格林函数和上下行延拓波场，应用反褶积成像条件提取地下成像点处成像值。

8、本发明提供的最小均方宽度约束的高斯束形态优化方法，与传统高斯束偏移方法相比，解决了近地表和中深层的成像精度矛盾，使得偏移成果剖面更加准确可靠，有利于后续解释处理。

9、优选地，步骤(2)中，利用最小均方宽度约束下的目标泛函得到所述对称矩阵参数，所述最小均方宽度约束下的目标泛函为：

10、

11、其中，s1,s2代表中心射线固定部分的任意两点，tr表示矩阵的迹，re表示取实部，g是加权矩阵，ψ(s)是为中间矩阵变量，即

12、

13、其中，加权矩阵g的形式为r(s)和y(s)分别表示矩阵ψ(s)的实部和虚部。

14、进一步优选地，步骤(3)中，所述最小化是通过公式(3)进行迭代求解：

15、

16、其中，o表示算式(3)的最小值，t为式(1)中的目标泛函，r0和y0分别为r(s)和y(s)在中心射线出射点位置上的初始矩阵，运算符||||2表示取矩阵的模的平方。

17、优选地，步骤(3)中，所述构建新型高斯波束是利用下式计算获得新型高斯波束函数u(s,n,ω)：

18、

19、其中，τ(s)是通过运动学射线追踪获取得到的走时，v(s)是输入模型速度场的值；p(s)、q(s)是射线追踪过程中获取的地震波束的动力学参量，(s,n)为射线中心坐标系，n表示旁轴射线在垂直于中心射线方向上的距离；ω表示波束频率。

20、进一步优选地，步骤(4)中，利用下式计算获得格林函数g(x,x′,ω)：

21、

22、

23、其中，φ(φ)为其积分权系数；uφ(x,x′,ω)为以角度φ出射的波束；x′,x分别表示波束的中心射线出射位置和地下目标成像点；a(x,x′)和t(x,x′)分别为地震波束的振幅、走时；π是圆周率；p1(s),p2(s)是复变量p(s)的两个分量，q1(s),q2(s)是复变量q(s)的两个分量，下标1表示虚部，下标2表示实部；ε(x)表示地下目标成像点x的复值波束参数；v(x′),v(x)分别是中心射线出射位置x′和地下目标成像点x的输入模型速度场的值；τ(x,x′)为从中心射线出射位置x′到地下目标成像点x的中心射线走时。

24、更优选地，步骤(4)中，由炮点xs、检波点xr处向下做射线追踪，构建炮检点上下行延拓波场：

25、

26、其中，vs、vr分别为炮点xs、检波点xr处速度；r(xr,xs,ω)为炮点xs激发检波点xr接收的地震记录；且有

27、φs＝αs-βs,φr＝αr-βr                            (8)

28、其中，αs和βs分别为炮点xs处的射线出射角和地表倾角；αr和βr分别为检波点xr处的射线出射角和地表倾角；pd表示炮点下行正传延拓波场、pu表示检波点上行反传延拓波场。

29、优选地，步骤(4)中，利用下式获得地下成像点处成像值：

30、

31、其中，i(x)表示地下成像点x处的成像值，上标*表示算子共轭。