面向旋转互质阵列的相干目标二维角度估计方法

本发明涉及雷达信号处理，特别涉及一种面向旋转互质阵列的相干目标二维角度估计方法。

背景技术：

1、雷达通常通过确定目标的二维角度参数，即方位角和俯仰角来实时获取目标位置信息，目标的角度参数估计是阵列信号处理领域的一个重要分支，是指利用阵列天线接收空域信号，通过统计信号处理方法以及优化方法对接收信号进行处理，以恢复发射信号包含的角度信息。

2、为了实现目标的二维角度估计，学者们大多在具有二维几何形状的阵列中进行研究，如l型和v型阵列。但在相同自由度要求下，此类型阵列所需要的阵元数较多，实际应用所受限制较多。此外，实际环境中所遇到的信号源之间往往不是独立的，具有一定的相关性，这将导致在doa估计时广泛应用的子空间类方法性能恶化甚至失效，所以相干信号源的doa估计也是此领域的一个重要课题。

技术实现思路

1、本发明提供一种面向旋转互质阵列的相干目标二维角度估计方法，可以提高二维角度估计精度和性能。

2、本发明第一方面实施例提供一种面向旋转互质阵列的相干目标二维角度估计方法，包括以下步骤：

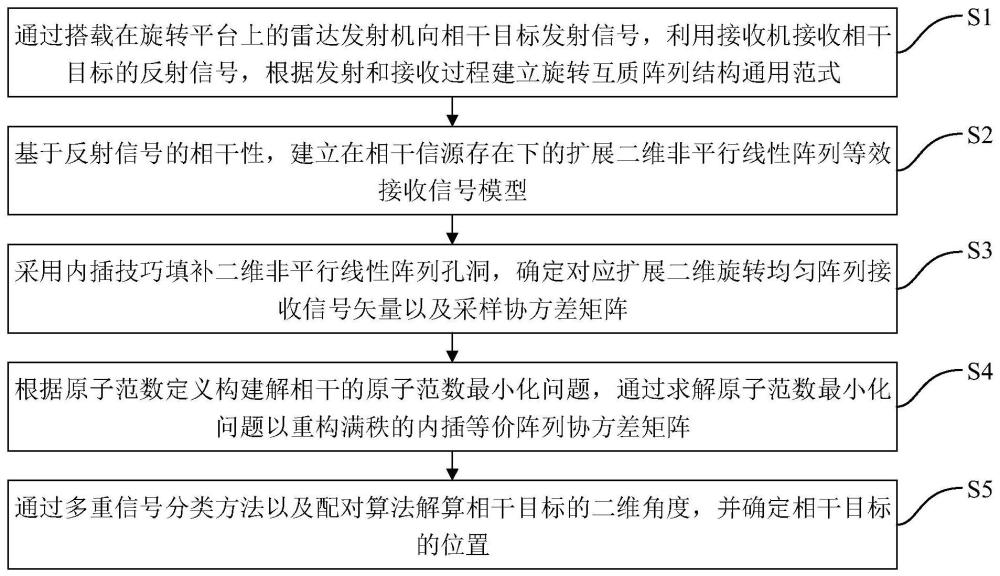
3、步骤s1，通过搭载在旋转平台上的雷达发射机向相干目标发射信号，利用接收机接收所述相干目标的反射信号，根据发射和接收过程建立旋转互质阵列结构通用范式；

4、步骤s2，基于所述反射信号的相干性，建立在相干信源存在下的扩展二维非平行线性阵列等效接收信号模型；

5、步骤s3，采用内插技巧填补二维非平行线性阵列孔洞，确定对应扩展二维旋转均匀阵列接收信号矢量以及采样协方差矩阵；

6、步骤s4，根据原子范数定义构建解相干的原子范数最小化问题，通过求解所述原子范数最小化问题以重构满秩的内插等价阵列协方差矩阵；

7、步骤s5，通过多重信号分类方法以及配对算法解算所述相干目标的二维角度，并确定所述相干目标的位置。

8、在本发明的一个实施例中，根据发射和接收过程建立旋转互质阵列结构通用范式，包括：

9、步骤s11，根据一维互质阵阵元位置信息，构建相干信源互质阵列模型，其中，增广互质阵有l个阵元，互质数组为(m,n)，m＜n且l＝2m+n-1，接收互质阵列由包含2m个阵元以及包含n个阵元的子阵组成，两个子阵的阵元间距分别为nd和md，单位阵元间距d取半波长，增广互质阵阵元为假设有q个方位角、俯仰角分别为的远场相干目标，旋转平台角速度为ω，采用笛卡尔坐标系，阵元位置表示为假设在平台旋转的极短时间内所检测相干目标相对于坐标系的到达角度不变，则时间t经过匹配滤波后的接收信号为：

10、

11、其中，s1(t)为参考信号，ηq为衰减因子，为相对相移，n(t)为加性高斯噪声，a为导向矩阵，有下式：

12、

13、

14、其中，ts为快拍数，c为光速；

15、步骤s12，对步骤s11中一维互质阵列进行旋转并在经过预设时间后对阵列信息进行采样，则阵列旋转前后的接收信号等效成二维阵列的接收信号，增广互质阵经过旋转时间τ后的阵元位置为表示经过旋转的阵列，经过旋转后的阵列接收信号表示为：

16、

17、其中，

18、b＝[b(θ1,φq),b(θ2,φq),…,b(θq,φq)]

19、

20、在本发明的一个实施例中，所述s2进一步包括：

21、步骤s21，令ωτ＝π/2，则旋转平台上互质阵阵元位置表示为：导向矢量为结合时刻t和t＝τ的导向矢量，得到一个合成的l型阵，令t＝0，则合成l型阵的导向矢量写为和

22、步骤s22，v型阵的夹角满足其中为v型阵阵元数，令则旋转平台上时刻t和t＝τ互质阵阵元位置分别为和则合成v型阵的导向矢量表示为以及

23、对接收信号补偿相位校正因子，以产生相位同步的接收信号向量，补偿后的接收信号表示为：

24、

25、其中，则旋转前后的接收信号x(t)以及y(t+τ)看作等价二维非平行线性互质阵列等效接收信号。

26、在本发明的一个实施例中，所述s3进一步包括：

27、步骤s31，采用内插技巧，将内插的虚拟阵元看作未处于工作状态的天线阵元，其对应接收信号为零，即：

28、

29、

30、其中，表示属于但不属于的元素集合，得到内插二维ula位于位置的阵元的接收信号以及对应导向矩阵为：

31、

32、

33、步骤s32，由内插过程可知，插值前后接收信号关系为以及其中g表示二值向量，用于区分参考虚拟阵列中推导而来的原始虚拟阵元与内插引入的虚拟阵元，其各元素值与参考虚拟阵列中的各个阵元一一对应：若该阵元为推导而来的原始阵元时，二值向量g中相应位置上的元素设置为1；反之，若该阵元是内插引入的虚拟阵元时，其相应位置上的元素设置为0，得到旋转前后阵列接收信号的采样协方差矩阵为：

34、

35、

36、其中，(·)h表示共轭转置操作算子，e[·]表示期望。

37、在本发明的一个实施例中，所述步骤s4进一步包括：

38、步骤s41，根据原子范数定义，构建原子范数最小化问题，采样协方差矩阵的原子范数表示为：

39、

40、

41、其中，表示原子范数，inf表示下确界，对进行最少原子数的原子分解时所重构的内插虚拟阵列协方差矩阵与理想矩阵拟合度最高，进而得到基于原子范数最小化的内插虚拟阵列协方差矩阵重构优化问题：

42、

43、

44、其中，为正则化系数，g＝ggt；

45、步骤s42，将所述原子范数最小化问题转化为半正定规划问题：

46、

47、

48、

49、

50、其中，为厄密特矩阵；

51、步骤s43，对所述半正定规划问题进行求解，得到满秩的内插等价阵列协方差矩阵：

52、

53、

54、在本发明的一个实施例中，所述步骤s5进一步包括：

55、步骤s51，将满秩的内插等价阵列协方差矩阵作为多重信号分类方法的输入以估计ψ和即：

56、

57、

58、其中，以及为协方差矩阵的噪声子空间，ax(ψ)和为旋转前后导向矢量，通过二维谱峰搜索得到空间谱的峰值，并将峰值从大到小排列，取前q个峰值对应的角度值即为波达方向的估计结果，所估计的方位角以及俯仰角分别为：

59、

60、

61、方位角、俯仰角对应的导向矩阵为

62、步骤s52，对所估计得的方位角及俯仰角进行配对，得到发射信号协方差矩阵由旋转前阵列协方差矩阵得到，为：

63、

64、其中，(·)+为伪逆操作，发射信号协方差矩阵由互协方差矩阵rφθ得到，为：

65、

66、设矩阵t为q×q维置换矩阵，则通过求解损失函数最小值以求解置换矩阵，得到的正确排布：

67、

68、求解最小二乘问题得到置换矩阵t，得到配对后的方位角及俯仰角为：

69、

70、步骤s53，基于所述配对后的方位角及俯仰角得到所述相干目标的位置。

71、本发明实施例的面向旋转互质阵列的相干目标二维角度估计方法，提出了旋转二维互质线性阵列的概念，以物理一维互质阵列搭载在旋转平台上，并对阵列信息进行采样得到等价二维阵列，从而估计目标二维参数。引入阵列插值将二维互质阵列转化成均匀阵列以利用接收信号的全部信息。引入原子范数最小化方法对协方差矩阵进行秩恢复，达到解相干的目的。最后通过music算法以及配对算法估计相干目标的方位角及俯仰角；与现有技术相比，本发明扩大了物理阵元的自由度，充分利用了非均匀阵列的全部信息，有效解决了相干性导致协方差矩阵缺秩的问题，有效提高目标二维角度估计精度。

72、本发明附加的方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。