基于多普勒频移测量的移动源定位方法

本发明涉及无线传感网络定位领域，尤其是涉及一种在考虑源频率误差和锚节点位置误差的情况下基于多普勒频移(doppler shifted frequency，dsf)测量的二维无线传感网络移动源定位方法。

背景技术：

1、无线传感网络(wireless sensor network，wsn)是一种分布式传感网络，一般由大量的传感器所组成，这些传感器分布在监测区域内，协作地感知、采集、处理和传输网络覆盖地理区域内被感知对象的信息。为了保持较低的执行成本，只有部分传感器装备有全球定位系统(gps)，这部分传感器称之为锚节点，而剩下的传感器则利用锚节点的已知位置，通过使用某种无线定位方案确定其位置，这些剩下的传感器称之为目标节点(也称之为源)。

2、移动源定位因在水声、自动驾驶和搜索救援等领域有着广泛的应用前景，因此成为了近十年来的研究热点。一般来说，源定位的目的是确定一个或者多个目标节点在二维或者三维空间中的位置或者速度信息，主要通过收集一系列测量值来构建定位问题，最常见的是基于时间的定位问题，包括到达时间(time of arrival，toa)或到达时间差(timedifference of arrival，tdoa)，而当源或锚节点移动时，相对运动使得系统会产生多普勒频移(doppler shifted frequency，dsf)或到达频率差(frequencydifference ofarrival，fdoa)，其中，时间测量信息和频率测量信息可以单独使用，也可以联合使用来进行源定位。通常来说，通过时间测量来定位源比使用频率观测更直接，因为频率观测不仅取决于时间测量中物体的位置，还取决于物体运动的速度，并且这两个未知量是耦合的。然而，当发射信号脉冲持续时间较长、带宽较窄时，频率观测的分辨率会比时间测量高得多，时间测量可能非常不准确或者难以测得，这使得对定位精度有着很大的影响。因此，在这种情况下，仅使用频率观测进行定位可能更为直接准确。此外，由于没有联合其他的测量信息，因此仅通过频率观测进行定位会比使用时间测量在计算上也更具吸引力与挑战性。

3、基于频率观测的定位场景有许多种情况，一种情况是当源在移动，而锚节点是静止时，在这种情况下考虑多普勒频移进行定位，采用计算量较大的数值网络搜索法来求解。如，i.shames等人在ieee transactions on aerospace and electronicsystems(电气和电子工程师协会(ieee)航空和电子系统汇刊)发表的成果中将多普勒频移测量模型以多项式优化形式表示，并采用软件优化包进行求解，该方法需假设源频率已知，且计算复杂度较高，难以满足对于定位实时性要求很高的场景，性能不是最优的。另一种情况是当源是静止的，锚节点以已知的速度移动时，这种情况已有许多与雷达通信和室内定位相关的应用，并且开发了许多不同复杂度和性能的解决方案。如，j.yin等人在ieee communicationletters(电气和电子工程师协会(ieee)通信学报)发表的成果中提出了一种迭代的方法来线性化fdoa测量方程，然而，如果源位置初始化不当，则不能保证收敛到全局最优，使得它们的逼近误差会显著增大。又如，y.pei等人在ieee communication letters(电气和电子工程师协会(ieee)通信学报)发表的成果中提出了一种仅基于fdoa的两步加权最小二乘(tswls)方法，该方法是以闭式解形式估计未知源位置，不需要对未知源位置进行任何初始解估计，然而该方法未考虑在实际环境中存在的锚节点位置误差会导致性能下降问题的影响，并且仿真结果表明该方法的定位精度还有提升空间。最后一种是源和锚节点都在移动的情况，文献中对这种情况下仅基于多普勒频移的源定位问题的分析研究相对较少，因此针对这种情况下，尤其是考虑到实际环境中锚节点位置的不准确性导致的性能下降问题，还需要进一步的理论研究。

技术实现思路

1、本发明所要解决的技术问题是提供一种针对源和锚节点都在移动的场景，在考虑移动源频率已知但受随机误差影响和存在锚节点位置误差的情况下，仅基于多普勒频移测量的二维无线传感网络移动源定位方法，其定位精度高。

2、本发明解决上述技术问题所采用的技术方案为：一种基于多普勒频移测量的移动源定位方法，其特征在于包括以下步骤：

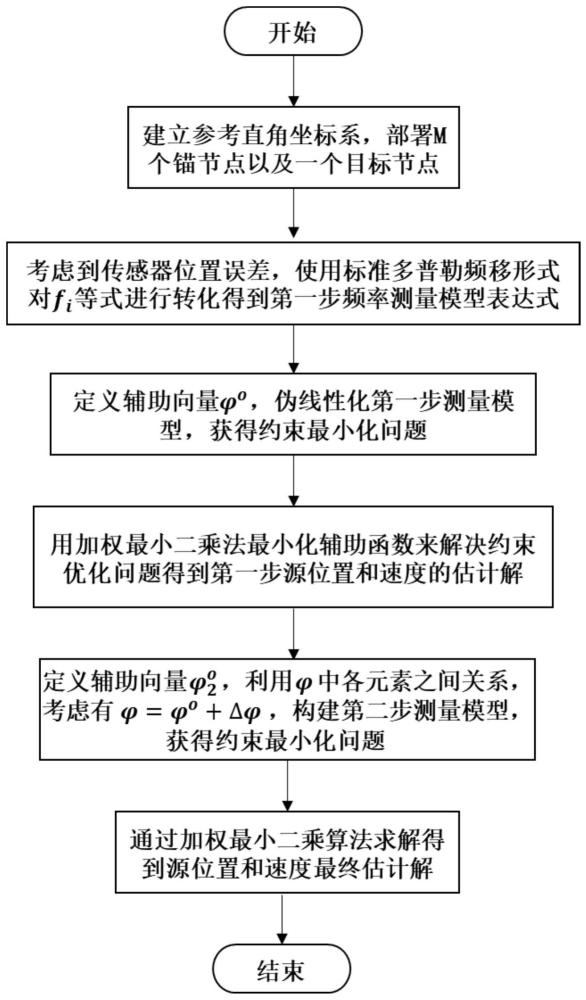
3、步骤1：在无线传感网络环境中，建立一个直角坐标系作为参考坐标系，并设定存在m个锚节点和一个移动源，将第i个锚节点在参考坐标系中的位置真实值和速度真实值对应记为和将移动源在参考坐标系中的位置真实值和速度真实值对应记为uo和uo＝[xo yo]t，再在第i个锚节点的位置误差δsi和速度误差存在的情况下，测量得到第i个锚节点在参考坐标系中的位置观测值和速度观测值，对应记为si和其中，m表示在无线传感网络环境中存在的锚节点的数量，m≥19，1≤i≤m，分别对应表示的第1个位置坐标分量、第2个位置坐标分量，分别对应表示的第1个速度坐标分量、第2个速度坐标分量，xo、yo分别对应表示uo的第1个位置坐标分量、第2个位置坐标分量，分别对应表示的第1个速度坐标分量、第2个速度坐标分量，上标“t”表示向量或矩阵的转置，si＝[xi yi]t，xi、yi分别对应表示si的第1个位置坐标分量、第2个位置坐标分量，分别对应表示的第1个速度坐标分量、第2个速度坐标分量；

4、步骤2：在无线传感网络环境中，由移动源发射测量信号，每个锚节点接收到测量信号后获得dsf测量值，将第i个锚节点的单次频率观测值记为fi，然后将所有锚节点的单次频率观测值组成一个矢量，记为f，f＝[f1 f2 … fm]＝fo+e；其中，表示移动源的频率真实值，满足fo表示移动源的频率观测值，δfo表示移动源的频率误差，δfo服从均值为0且方差为的高斯分布，c表示信号传播速度，符号“||||”为求欧几里得范数符号，ei表示fi中的观测噪声，fo表示f的真实值的矢量形式，e为观测噪声矢量，e服从均值为0且协方差矩阵为qe的高斯分布，e＝[e1 e2 … em]；

5、步骤3：令rio表示第i个锚节点与移动源之间的真实距离，rio＝||uo-si||，然后对δsi进行泰勒级数展开，有：再将代入中，得到其中，i＝1,2,...,m，εi为复合噪声项，εi的矢量形式为gf为m维的向量，gf中的第i个元素表示为(gf)i，gs和均为m×2m维的矩阵，gs中由第i行及第2i-1列至第2i列的元素构成的子矩阵表示为(gs)(i,2i-1:2i)，gs中除了(gs)(i,2i-1:2i)外的其余元素均为0，pio表示的正交投影矩阵，i表示2m×2m维的单位矩阵，中由第i行及第2i-1列至第2i列的元素构成的子矩阵表示为中除了外的其余元素均为0，ε服从均值为0且协方差矩阵为qε的高斯分布，e[]表示求数学期望，令δβ服从均值为0且协方差矩阵为qs的高斯分布，qs＝e[δβδβt]；

6、步骤4：令di表示标准化多普勒频移公式即然后结合将改写成高度非线性方程，描述为：再引入辅助量，将高度非线性方程转化为伪线性方程组，并忽略二阶及以上的高阶噪声项后用矩阵形式表示为：最后根据得到加权最小二乘优化问题，描述为：并求解得到加权最小二乘解，即的解其中，i＝1,2,…,m，ri表示第i个锚节点与移动源之间的观测距离，符号表示对应元素相乘，diag{}表示生成以{}中的向量元素为对角线元素的对角矩阵，min为取最小值函数，u表示移动源在参考坐标系中的位置观测值，表示移动源在参考坐标系中的速度观测值，u＝[x y]t，x、y分别对应表示u的第1个位置坐标分量、第2个位置坐标分量，分别对应表示的第1个速度坐标分量、第2个速度坐标分量，j表示加权最小二乘优化问题中的代价函数，

7、步骤5：引入向量令并引入向量h2，令然后利用中的各元素间的关系，并考虑到忽略二阶及以上的高阶噪声项后得到再根据得到加权最小二乘优化问题，描述为：并求解得到加权最小二乘解，即的解进而得到移动源的位置和速度各自的估计值；其中，表示步骤4中得到的的解中的第1个元素至第19个元素构成的向量，表示的误差，a2为19×4维的矩阵，a2中由第1行至第4行的元素构成的子矩阵表示为(a2)(1:4,:)，(a2)(1:4,:)＝i4，i4表示4×4维的单位矩阵，a2中由第5行至第8行的元素构成的子矩阵表示为(a2)(5:8,:)，blkdiag{}表示生成以{}中的元素为对角线元素的对角矩阵，表示步骤4中得到的的解中的第1个元素至第4个元素构成的向量，a2中由第9行至第10行的元素构成的子矩阵表示为(a2)(9:10,:)，表示步骤4中得到的的解中的第2个元素，表示步骤4中得到的的解中的第4个元素，a2中由第11行至第14行的元素构成的子矩阵表示为(a2)(11:14,:)，分别对应表示步骤4中得到的的解中的第5个元素、第6个元素、第7个元素、第8个元素、第9个元素、第10个元素，o2×2表示2×2维的零矩阵，a2中由第15行至第18行及第1列至第2列的元素构成的子矩阵表示为(a2)(15:18,1:2)，表示步骤4中得到的的解中的第3个元素，a2中由第19行及第1列至第2列的元素构成的向量表示为(a2)(19,1:2)，和对应表示步骤4中得到的的解中的第11个元素和第12个元素，a2中除上述元素外的其余元素均为0，b2＝i19-c，i19表示19×19维的单位矩阵，c中由第5行至第8行及第1列至第4列的元素构成的子矩阵表示为c(5:8,1:4)，c中由第9行至第10行及第2列至第4列的元素构成的子矩阵表示为c(9:10,2:4)，表示步骤4中得到的的解中的第1个元素，c中由第11行至第14行及第5列至第8列的元素构成的子矩阵表示为c(11:14,5:8)，表示步骤4中得到的的解中的第1个元素至第2个元素构成的向量，表示步骤4中得到的的解中的第3个元素至第4个元素构成的向量，c中由第11行至第14行及第9列至第10列的元素构成的子矩阵表示为c(11:14,9:10)，c中由第15行至第18行及第3列至第4列的元素构成的子矩阵表示为c(15:18,3:4)，c中由第19行及第11列至第12列的元素构成的向量表示为c(19,11:12)，c中除上述元素外的其余元素均为0，

8、所述步骤4中，在求解加权最小二乘优化问题时，先令w1＝i，求解加权最小二乘优化问题得到的的值作为的初始值；再将的初始值代入加权最小二乘优化问题中，再次求解，求解得到加权最小二乘解，即的解

9、与现有技术相比，本发明的优点在于：

10、本发明方法通过将基于两步法准则的最小化问题每个阶段进行优化，这样不存在以往穷举网格搜索法的高计算复杂度以及传统线性迭代方法那样的初始化问题，并且避免了局部收敛问题。存在锚节点位置误差以及移动源频率已知但受随机误差影响的情况，在第一阶段根据dsf测量值，通过引入多个辅助变量将高度非线性方程转化为伪线性形式，得到加权最小二乘优化问题，从而得到初步的次优估计解，在第二阶段考虑干扰参数与移动源位置和速度间的关系，对第一步的估计误差来构建第二步的测量模型，进而得到加权最小二乘优化问题，利用加权最小二乘方法求解得到未知源的最终估计解。当发射信号脉冲持续时间较长、带宽较窄时，频率测量的分辨率会比时间测量高得多，时间测量可能非常不准确或者难以测得，这使得对定位精度有很大的影响。因此，在这种情况下，仅使用频率测量进行定位可能更为直接准确。此外，由于没有联合其他测量信息，仅通过频率观测进行定位会比使用时间测量在计算上也更具挑战性。而且该方法的仿真环境是移动源和锚节点都在移动的情况，针对该场景下，考虑了在实际环境中存在的锚节点位置误差会导致性能下降问题的影响，进一步提升了定位精确度，从而更加准确地估计出移动源的位置和速度，而且在较大测量值噪声功率的情况下性能依然稳定。