一种惯性坐标系ZEM制导闭环净加速度指令幅值的解析方法与流程

本发明涉及精确制导，特别是zem制导闭环系统中、由初始zem误差引起的加速度指令幅值，即净加速度指令幅值的解析方法。

背景技术：

1、闭环制导系统的解析解或闭合解对研究制导系统状态的固有特性、控制量需求、制导算法改进等十分重要，也是精确制导领域面临的难点理论问题(li hongyan,taohong,wang jiang,he shaoming.three-dimensional optimal guidance withoutterminal maneuverability advantage.journal of guidance control and dynamics,apr 2023,doi:10.2514/1.g007483)。即使对传统的比例导引(pn proportionalnavigation)、增广比例导引(apn augmented pn)、纯比例导引ppn(pure pn)、真比例导引tpn(true pn)，基于zem(zero miss distance)误差的制导等，目前也仅仅知道闭环系统的稳定性和特殊情况下的解析解，一般情况仍然只能得到某种意义的近似解(koray s ererand raziye tekin.impact vector guidance.journal of guidance control anddynamics,oct.2021,pp.1892-1901)。

2、实际上，解决传统制导的解析解问题必须首先解决平行接近制导的理论问题，因为平行接近制导相关概念和理论对准确描述制导系统状态有十分重要的指导作用。平行接近制导面临的主要困难在于缺乏基本的理论基础。n a shneydor在1998年出版的《missileguidance and pursuit:kinematics,dynamics and control》(isbn 1-898563-43-8，1998，horwood publishing limited，west sussex，england)一书虽然研究了平行接近法制导问题(见第四章“chapter4.parallel navigation”)，但并没有给出制导算法。西北工业大学杨军教授在其著作《现代防空导弹制导控制技术》(isbn 9787561241943，2014，西北工业大学出版社)中指出平行接近法在实际应用上比较困难，真正实现平行接近法的实例还很少见(见p50-p51)。印度理工学院(indian institute of science)宇航工程系(department of aerospace engineering)的debasish ghose教授在2015年的讲义《guidance theory and applications》中指出比例导引是实现平行接近法的合理途径(“proportional navigation(pn)guidance—most logical way to implement constantbearing course”，见lecture 3，p14)。li-chen，wei-der chang，dung-ming chuang等人按照视线角速度指数收敛为基准提出了一种平行接近法制导律(a nonlinear constantbearing guidance and adaptive autopilot design for btt missiles[c].proceedings of the american control conference,albuquerque,new mexico june1997,pp:2774-2778)，但理论上无法证明它满足平行接近法的关键制导特性，且仿真结果与平行接近法不符，仅与比例导引类同。北京航天微系统研究所的zhigao liu工程师以视线角速度为零的代数方程为基准研究了一种平行接近制导律(constant bearingguidance law for homing missiles[c].2017 10th international symposium oncomputational intelligence and design(iscid)ieee,2017,pp:247-251)，其仿真结果与平行接近法相差甚远。

3、借助平行接近制导相关理论研究比例导引、增广比例导引、纯比例导引、真比例导引、zem制导问题等，解决闭环系统状态的解析求解问题对精确制导技术具有重要意义。

4、制导指令一般包含：与制导误差直接相关的主控制量，直接影响制导误差的因素形成的补偿控制量，抵消目标机动影响的补偿控制量。不计目标机动补偿控制的指令部分属于净指令，它纯粹由拦截的相对运动引起。对zem制导，净加速度指令简单而言就是由zem误差引起的加速度指令部分。净加速度指令的幅度是制导系统控制量需求分析的核心，对制导系统设计十分重要。

技术实现思路

1、本发明的技术解决问题是：对惯性坐标系描述的zem制导，本发明提出一种闭环系统zem误差幅值和净加速度指令幅值的解析方法。

2、本发明的解析方法的先决条件如下。

3、条件一，本发明所有计算方法均建立在惯性直角坐标系。本发明所谓的惯性直角坐标系也可简称为惯性坐标系，且坐标系体轴的方向可根据实际需要自由选择。拦截器和目标的绝对位置、绝对速度矢量和绝对加速度矢量等均在该惯性坐标系进行度量。

4、条件二，本发明根据惯性坐标系下拦截器和目标的绝对位置矢量、绝对速度矢量及绝对加速度矢量来定义两者的相对位置矢量、相对速度矢量和相对加速度矢量。拦截器与目标间的相对位置矢量、相对速度矢量和相对加速度矢量计算方法为：相对位置矢量是目标的绝对位置矢量减去拦截器的绝对位置矢量，相对速度矢量是目标的绝对速度矢量减去拦截器的绝对速度矢量，相对加速度矢量是目标的绝对加速度矢量减去拦截器的绝对加速度矢量。相对位置、相对速度和相对加速度属于瞬时物理量。本发明的视线指拦截器到目标的连线，视线与拦截器与目标的相对位置矢量方向一致。视线在惯性空间的转动速度称为视线角速度。

5、条件三，本发明所谓的zem是英文zero effort miss-distance的缩写，一般译为零控脱靶量或零作用脱靶量，但通常直接使用zem表示。zem制导就是以zem误差(一种预测的相对位置误差)进行制导指令形成的制导方法，当然也可以按照线性化拦截系统模型基于最优控制原理得到，可归类为二次性能最优制导律，即指标函数为脱靶量和控制平方积分最小。本发明所提的修正zem制导是一种为提高闭环系统收敛性，在zem误差引入估计的相对速度校正因素而形成的一种新的zem计算方法。

6、条件四，本发明所谓的平行接近法、平行接近法制导或平行接近制导具有相同的意义。在制导过程中，能够使视线角速度快速归零并始终维持为零的制导方法称为平行接近制导。本发明称平行接近制导的误差为制导失调角。视线角速度不为零的状态称为制导失调。

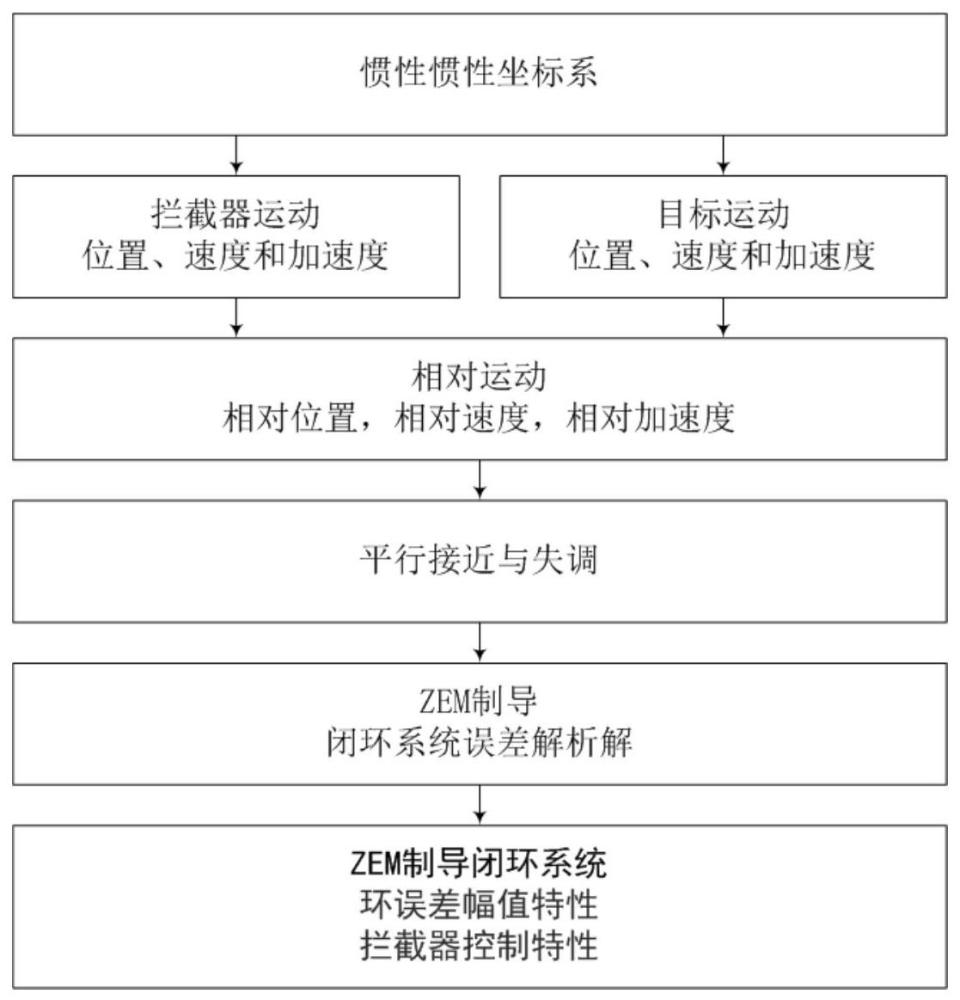
7、本发明所提出的zem制导闭环净加速度指令幅值的解析方法的实现过程为：

8、步骤一：坐标系定义、变量表示和相对运动计算；

9、步骤二：平行接近与制导失调；

10、步骤三：zem制导和闭环解析解。

11、步骤四：zem制导闭环误差幅值特性与控制特性。

12、本发明与现有技术相比有益效果为：

13、(1)建立了zem制导闭环系统误差幅值的解析计算关系，它是初始瞄准误差和初始失调角的函数。

14、(2)建立了zem制导闭环系统净加速度指令幅值的解析计算关系。根据净加速度指令解析关系得到，保证拦截器加速度指令幅值衰减、且衰减速度最慢的模式为线性衰减，这时需求的最小导航比为3，这也是对比例导引最优导航比为3的另外一种理论解释。

15、(3)本发明对完善zem制导理论和应用有重要作用。