一种用于多普勒量测的预观测整体融合跟踪方法

本发明属于多普勒雷达目标跟踪，尤其涉及一种用于多普勒量测的预观测整体融合跟踪方法。

背景技术：

1、多普勒雷达由于可在频域去噪，其抗干扰抗杂波能力强于普通雷达，因此，多普勒雷达被广泛运用于目标跟踪、战场侦察和交通管制等领域。

2、在进行目标跟踪时，多普勒雷达除了能获得目标的距离和方位角，还能获得目标的多普勒量测即径向速度。多普勒量测是多普勒雷达所有测量值中唯一包含目标速度信息的测量值，研究表明，充分利用多普勒量测可以有效提高目标跟踪精度。然而，由于借助雷达量测实施运动目标跟踪时，通常采用笛卡尔坐标系下的物理量来刻画目标运动状态，而多普勒雷达提供的测量即距离、方位角和多普勒量测都是极坐标系下的量值，坐标系变换在目标运动状态与雷达量测之间引入了难于消除的非线性，量测的非线性无疑会增加跟踪系统复杂度、导致算法估计性能下降。因此，解决目标状态和测量非线性是目标跟踪的主要问题。

3、为解决带多普勒量测的雷达目标跟踪问题，通常采用以下非线性滤波：

4、序贯扩展卡尔曼滤波(sekf)，先使用量测转换卡尔曼滤波对位置量测进行线性滤波，再利用ekf处理多普勒量测。然而，由于ekf线性化过程中舍弃了二阶以上的高阶项，所以处理较强非线性时引起的误差较大。

5、序贯无迹卡尔曼滤波(sukf)，先对具有量测误差相关性的距离和多普勒量测进行解相关处理，再利用ukf对位置量测和伪多普勒量测进行序贯处理。缺点是无迹卡尔曼滤波参数的选择问题尚没有得到完全解决。

6、带多普勒量测的转换测量卡尔曼滤波(cmkfrr)，该方法将距离、角度和多普勒量测转到笛卡尔坐标系中的位置和速度，这种转换是无偏和一致的，但是该测量转换需要事先了解切向速度的分布。

7、这些方法虽然在一定程度上提升了多普勒雷达的目标跟踪效果，但是在跟踪精度和计算量上仍有提升空间。

8、因此，提出一种用于多普勒量测的预观测整体融合跟踪方法，来解决现有技术存在的困难，是本领域技术人员亟需解决的问题。

技术实现思路

1、本发明提出一种用于多普勒量测的预观测整体融合跟踪方法，合理利用了多普勒量测信息且避免了非线性滤波对估计精度的影响，能有效提高目标跟踪性能。

2、为了实现上述目的，本发明采用如下技术方案：

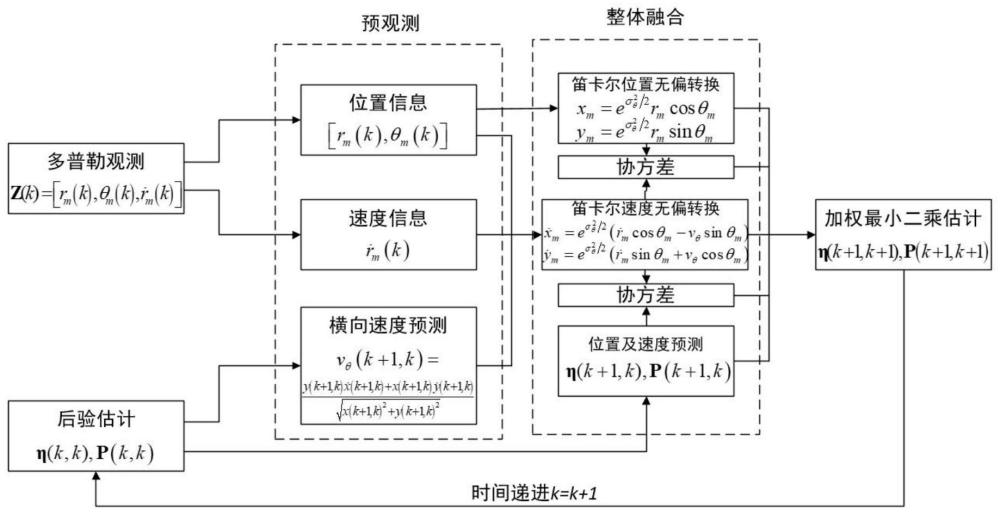
3、一种用于多普勒量测的预观测整体融合跟踪方法，获取k时刻目标状态的后验估计均值和协方差，则k时刻到k+1时刻的滤波具体步骤如下：

4、s1：获取目标运动数据，构建匀速直线运动模型和匀加速直线运动模型，并在笛卡尔坐标系下分别对匀速直线运动模型和匀加速直线运动模型的目标状态及其协方差进行一步预测；

5、s2：对s1中得到的匀速直线运动模型和匀加速直线运动模型的目标状态及其协方差一步预测来计算量测预测及其协方差；

6、s3：获取目标多普勒雷达测量值并将多普勒雷达测量值转到笛卡尔坐标，并计算量测转换误差协方差；

7、s4：在匀速直线运动模型和匀加速直线运动模型中通过加权最小二乘法线性融合s2中计算结果和s3中计算结果完成当前时刻目标跟踪状态和协方差的更新；

8、s5：循环执行步骤s1-s4，直至目标跟踪完成。

9、上述的方法，可选的，s1中具体内容为：

10、在笛卡尔坐标下对匀速直线运动模型目标状态和协方差一步预测的具体过程为：

11、xcv(k+1,k)＝φcv(k)xcv(k,k)；

12、ρcv(k+1,k)＝φcv(k)ρcv(k,k)φcv(k)t+γcv(k)qcv(k)γcv(k)t；

13、

14、

15、式中，表示k时刻目标的状态估计，x、y和为目标的位置和速度；xcv(k+1,k)表示k+1时刻目标的状态预测；ρcv(k,k)表示k时刻目标的估计协方差；ρcv(k+1,k)表示k+1时刻目标的一步预测协方差；φcv(k)为状态转移矩阵，γcv(k)为过程噪声驱动矩阵，qcv(k)为过程噪声；

16、笛卡尔坐标下对匀加速直线运动模型目标状态和协方差一步预测的具体过程为：

17、xca(k+1,k)＝φca(k)xca(k,k)；

18、ρca(k+1,k)＝φca(k)ρca(k,k)φca(k)t+γca(k)qca(k)γca(k)t；

19、

20、

21、式中，表示k时刻目标的状态估计，为目标的加速度；xca(k+1,k)表示k+1时刻目标的状态预测；ρca(k,k)表示k时刻目标的估计协方差；ρca(k+1,k)表示k+1时刻目标的一步预测协方差；φca(k)为状态转移矩阵，γca(k)为过程噪声驱动矩阵，qca(k)为过程噪声。

22、上述的方法，可选的，s2中计算量测预测及其协方差具体公式如下：

23、

24、

25、

26、

27、

28、式中，rc、θc、和分别为距离预测、角度预测、径向速度预测和切向速度预测；和为对应协方差；为状态一步预测值，p(k+1,k)为协方差一步预测值，p2×2(k+1,k)为p(k+1,k)的前2行2列。

29、上述的方法，可选的，s3中具体内容为：

30、将目标多普勒测量值转换为笛卡尔坐标：

31、

32、对上式计算期望：

33、

34、

35、

36、

37、无偏量测转换为：

38、

39、式中，xm、ym和为笛卡尔坐标系中的量测转换值，上式共为匀速直线运动模型和匀加速直线运动模型的测量转换。

40、上述的方法，可选的，量测转换误差协方差具体表示为：

41、

42、式中，

43、

44、

45、

46、

47、

48、

49、

50、

51、

52、

53、上述的方法，可选的，s4的具体内容为：构建匀速直线运动模型的线性回归模型为：

54、

55、将上述矩阵方程记为ax＝b+e，e的协方差var(e)记为v，则有：

56、

57、

58、状态更新：xcv(k+1,k+1)＝(atv-1a)-1atv-1b；

59、协方差更新：ρcv(k+1,k+1)＝(atv-1a)-1；

60、其中，x、y和为笛卡尔坐标系中位置和速度的后验估计；为状态一步预测值；xm、ym和为笛卡尔坐标系中的量测转换值；为一步预测协方差；为量测转换协方差；

61、上述的方法，可选的，s4的具体内容为：

62、构造匀加速直线运动模型的线性回归模型为：

63、

64、

65、将上述矩阵方程记为ax＝b+e，e的协方差var(e)记为v，则有：

66、

67、

68、状态更新：xca(k+1,k+1)＝(atv-1a)-1atv-1b；

69、协方差更新：ρca(k+1,k+1)＝(atv-1a)-1；

70、其中，x、y、和为笛卡尔坐标系中位置、速度和加速度的后验估计；和为状态一步预测值；xm、ym、和为笛卡尔坐标系中的量测转换值；为一步预测协方差，由s1得到；为量测转换协方差。

71、经由上述的技术方案可知，与现有技术相比，本发明一种用于多普勒量测的预观测整体融合跟踪方法，具有以下有益效果：

72、本发明采用与以往算法完全不同的技术思路，将位置量测和多普勒量测转到笛卡尔坐标系，使状态与观测呈线性关系，最后通过加权最小二乘线性融合获得每时刻目标状态后验估计。克服了多普勒量测和目标状态间的强非线性，能够以较小的计算量对目标跟踪，可以很好地提高目标跟踪精度。