一种高压继电器小子样寿命评估方法、系统、装置及介质

本发明属于电动汽车高压电气系统可靠性，涉及一种高压继电器小子样的寿命评估方法、系统、装置及介质，具体涉及基于平均秩次法的经验分布函数参数估计、基于全最小二乘法的故障分布函数参数估计、线性相关性检验、拟合性检验及基于均方根误差、相对均方根误差的可靠性模型优选和寿命评估。

背景技术：

1、新能源汽车高压继电器是隔离大电流的自动开关元件，其功能保持性即可靠性直接影响整车使用的安全性和寿命。高压继电器产品结构复杂，试验成本高的特点，致使其难以进行批量试验，短期内寿命数据的获取变得困难。因此，如何充分利用有限小样本信息来实现产品寿命评估成为目前急需解决的一个重要问题。

2、当前解决故障样本数据不足问题的常用方法包括贝叶斯自助法、改进的扩展理论和修正的经验分布函数。贝叶斯自助法要求利用先验信息建立分布模型，并基于小数据估计可靠性指标和参数；这种方法可以在小样本情况下取得较好的结果，但其先验信息往往是通过经验确定的，这不仅会产生不可避免的主观误差。扩展理论基于自抽样方法来增加样本信息，提高参数估计的精度；这种扩展方法限于区间内部，只能从左向右扩展数据；而且，参数对样本的过度依赖可能导致实际应用中的重大偏差。基于径向基函数(rbf)神经网络的bootstrap数据增强方法和基于bootstrap数据增强的b-mle方法存在收敛速度慢、网络结构选择不一致和局部极小化等问题。学者们已经应用支持向量机(svm)等计算机学习方法来分析可靠性，svm本身对样本误差极其敏感，且缺乏自适应能力，这会大大降低可靠性分析的稳健性。贝叶斯方法和bootstrap方法结合并没有解决这两种方法原有的缺点。

3、分布类型的参数估计方法可分为图估计法、矩法、最大似然法、差分进化法、贝叶斯法、灰色模型法和最小二乘法。这些方法大多没有解析解，需要求解非线性方程组或多元函数的最大值点。灰色模型方法可以一次估计三参数威布尔分布的三个参数而无需迭代，避免了参数之间的相关性问题，且具有较快的计算速度，适合于小样本威布尔分布数据分析；但该方法的灰色模型原理将其故障数据秩次限制为整数，因此不适用于数据缺失的小样本情况。最小二乘法由于其简单的原理、解析解不依赖初始值而被广泛使用。

4、工程实践中多假设分布模型是双参数威布尔分布。参数估计的最小二乘法的原理是将分布函数线性化，用经验分布函数代替，将其转换为一元线性回归方程，并通过回归系数估计威布尔分布的参数。经验分布函数的不同选择会导致单变量模型的不同，从而导致估计参数的不统一。应用最佳经验分布来计算分布函数的实际值，并使用总体最小二乘准则来克服这一缺点。针对多辆电动汽车的随机截尾可靠性试验下高压继电器失效数据小样本、高截尾的特点，提出一种集成平均秩次法、全最小二乘的汽车继电器可靠性建模及寿命评估方法。

技术实现思路

1、针对小样本、高截尾数据下现有技术因直接应用近似中位秩计算经验分布函数，采用最小二乘法估计参数带来的模型偏差，本发明提供一种基于最优经验分布函数、全最小二乘法的继电器小样本可靠性建模及寿命评估方法，利用该方法对继电器寿命评估，误差更小、更符合实际。

2、为解决上述技术问题，本发明是采用如下技术方案实现的，结合附图1说明如下：

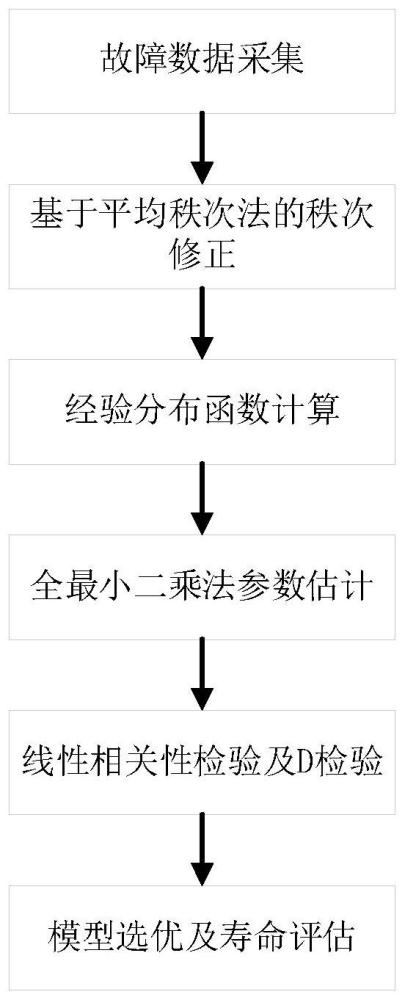
3、一种小子样高压继电器寿命评估方法，包括下述步骤：

4、步骤一、进行电动汽车电气系统组件划分；根据采集的电动汽车试验下故障信息，借助于数据计算、故障致因分析和系统结构功能方面的相关经验确定继电器故障间隔里程数据及截尾数据；

5、步骤二、基于平均秩次法的故障间隔里程数据秩次修正；

6、步骤三、经验分布函数值计算；

7、步骤四、基于全最小二乘法估计分布模型参数估计；

8、步骤五、线性相关检验与d检验；

9、步骤六、基于最小均方根误差和相对均方根误差的最佳分布模型选择与寿命评估。

10、步骤二中所述的基于平均秩次法的故障数据秩次修正是指：

11、随机截尾试验下继电器除了有n个故障间隔里程数据，还有m个右截尾数据。考虑截尾数据对故障数据顺序号影响，采用平均秩次法，对m+n个数据从小到大排列，记这列编号为j；然后，只对n个故障数据排列，记这列编号为i，则修正后第i个故障间隔里程数据的顺序号用式(1)计算：

12、ri＝ri-1+(m+n+1-ri-1)/(m+n+2-j)                        (1)

13、式中：r0＝0

14、步骤三中所述的经验分布函数计算是指；

15、经验分布函数f(ti)分别采用平均平方距离最小估计、期望估计、中点估计、中位秩估计和近似中位秩估计：

16、平均平方距离最小估计：

17、

18、期望估计：

19、

20、中点估计：

21、

22、中位秩估计：

23、

24、近似中位秩估计：

25、

26、式中：n—所有数据个数，包括故障间隔里程数据与截尾数据，即n＝m+n

27、公式(3)、(4)、(5)、(6)、(7)中的i由公式(1)计算得到的ri代替，就可以计算出每个故障间隔里程数据对应的经验分布函数。

28、公式(3)至公式(7)左边的字母分别表示平均平方距离、期望、中点、中位秩、近似中位秩。

29、步骤四所述的基于全最小二乘法估计分布模型参数估计是指；

30、对假设分布模型进行必要的变换使其线性化，设线性回归方程为：y＝ax+b；然后应用全最小二乘原理，通过公式(8)求得假设分布模型参数的估计值全最小二乘法是最小化从一个点到拟合线的垂直残差平方和，即获得线性模型的总体最小二乘参数估计。

31、

32、式中：分别是变量xi和yi的平均值。

33、式(8)中±的确定取决于分布。如果样本协方差大于0，则取“+”；如果小于0，则取“-”。

34、步骤五所述的线性相关性检验与d检验是指：

35、采用公式(9)计算两变量x,y的线性相关系数：

36、

37、当时，则认为x与y之间是线性相关的。其中ρα是相关系数起码值，当显著性水平α＝0.1时，相关系数起码值近似为

38、当则认为x与y之间是线性相关的，即故障数据服从假设分布。

39、d检验法是通过对两个分布之间的差异的分析，判断样本的观察结果是否来自假设分布的总体。d检验具有分布无关性，它的临界值并不依赖于特定分布。

40、将获得的n个故障间隔里程数据按照由小到大的规则进行排序，依据拟合得到的假设的分布f0(ti)和经验分布函数f(ti)，根据公式(10)计算检验统计量dn的观察值。

41、dn＝max|f(ti)-f0(ti)|                      (10)

42、将dn的观察值和临界值dn,α进行比较，dn,α临界值可以通过查表或利用近似公式计算得到，如果dn≤dn,α，则认为原假设可以接受，即故障间隔里程数据服从假设分布模型，否则拒绝原假设。

43、步骤六所述的基于最小均方根误差和相对均方根误差的最佳分布模型选择与寿命评估是指：

44、依据公式(11)、(12)计算故障间隔里程数据服从分布与经验分布函数的均方根误差rmse和相对均方根误差mrmse，以均方根误差和相对均方根误差最小的分布确定最佳分布，最佳分布对应的经验分布函数是最优经验分布函数；

45、

46、

47、依据得到的最优故障分布函数f(t)，进行寿命评估，采用公式(13)计算平均故障间隔里程mtbf

48、

49、当最优分布模型为威布尔分布时，即则根据形状参数β和伽马函数γ(1+1/β)，以及尺度参数η，计算出平均故障间隔里程

50、与现有技术相比本发明的有益效果是：

51、本发明考虑了截尾数据的影响，引入平均秩次法计算故障间隔里程数据的顺序号，在此基础上采用期望估计、中点估计、中位秩估计和近似中位秩估计进行经验分布函数计算，应用全最小二乘法进参数估计，提高参数估计的稳健性，在线性相关性检验和d检验验证基础上，引入均方根误差、相对均方根误差识别故障间隔里程最优分布并进行寿命估计，提高寿命估计精度。