基于特征融合与FCM算法的轴承故障诊断方法

本发明涉及轴承故障诊断，具体涉及一种基于特征融合与fcm算法的轴承故障诊断方法。

背景技术：

1、旋转机械属于最常见的机械设备之一，在社会生活、工业生产、国防军事等多个领域中都有着广泛应用，而滚动轴承作为旋转机械的关键部件，其状态对系统的正常运行起着至关重要的作用。一些轻微的轴承故障就可能导致系统运行异常，而严重的轴承故障甚至会引发安全事故造成人身财产的巨大损失。引起轴承故障的因素有很多，如老化、磨损、超负荷运行、操作失误等，以至于有些轴承故障是瞬时产生的，而有些则是长期缓慢积累引起的，由此导致轴承故障类型多样且复杂，引起的故障程度也有差别。

2、采集和分析滚动轴承运行时的振动信号以监测与诊断其工作状态是一种常用的故障诊断方法。针对轴承振动信号可以从时域和频域的角度进行分析，但如果仅从时域或频域的角度分析轴承振动信号，由于割裂了时域与频域的联系，很难获得信号特征的全貌，而从联合的时频域来分析，则可以提供时频域的综合信息，能够提高诊断的准确性和可靠性。并且不同的旋转机械系统其轴承运行时产生的振动信号存在差异，单一固定的对某一个或几个时域与频域特征进行分析具有较大的局限性，无法应用在不同的旋转机械系统中。同时，要具体的分析故障信息不仅需要区分正常轴承与故障轴承，还要能够对轴承的故障类型和故障程度进行诊断。

技术实现思路

1、针对上述问题，本发明提出了一种基于特征融合与fcm算法的轴承故障诊断方法，通过对轴承振动信号进行时域和频域分析，得到多个时域特征与频域特征，并在此基础上进行类别可分性比较，筛选出优势特征，再将优势特征进行降维融合得到综合特征，对其进行聚合分类后区分出正常轴承信号与各类故障轴承信号，同时根据聚类中心还能够对故障程度进行判别；有效提高轴承故障诊断的准确性和可靠性。

2、本发明采取的技术方案为：

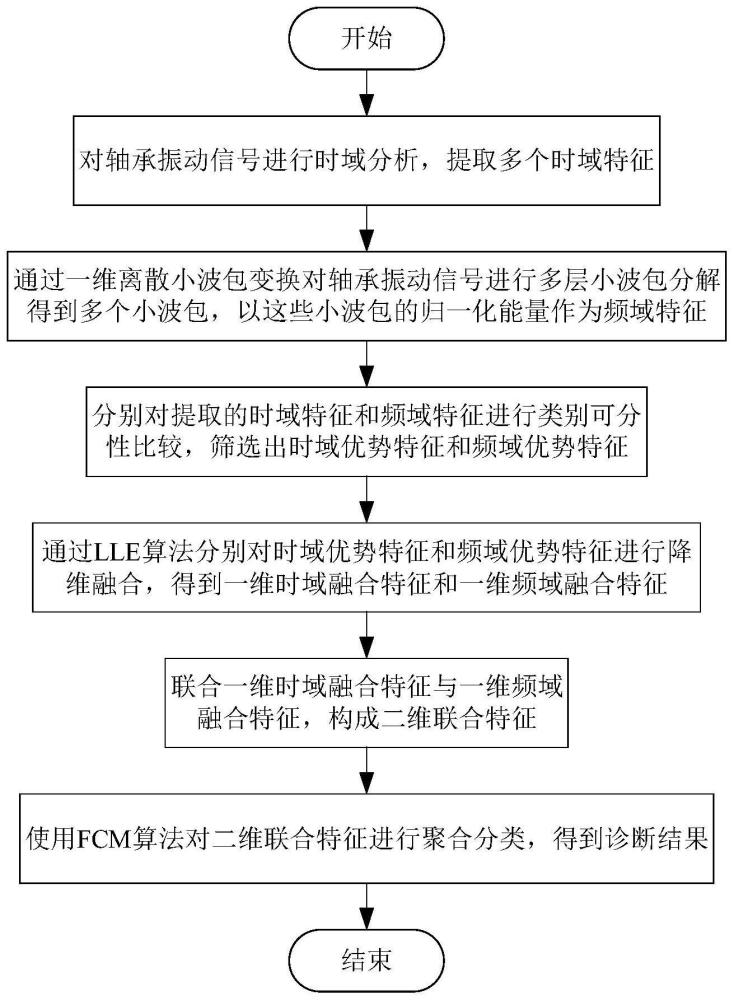
3、基于特征融合与fcm算法的轴承故障诊断方法，包括以下步骤：

4、步骤1：对轴承振动信号进行时域分析，提取多个时域特征；

5、步骤2：通过一维离散小波包变换对轴承振动信号进行多层小波包分解，得到多个小波包，以这些小波包的归一化能量作为频域特征；

6、步骤3：分别对步骤1提取的时域特征和步骤2提取的频域特征进行类别可分性比较，筛选出时域优势特征和频域优势特征；

7、步骤4：通过lle算法分别对时域优势特征和频域优势特征进行降维融合，得到一维时域融合特征和一维频域融合特征；

8、步骤5：联合步骤1所得一维时域融合特征与一维频域融合特征，构成二维联合特征；

9、步骤6：使用fcm算法对步骤5得到的二维联合特征进行聚合分类，得到诊断结果。

10、所述步骤1中，对轴承振动信号进行时域分析后提取的时域特征共15个，其中，有量纲指标10个，分别为均值、有效值、方根幅值、绝对平均值、歪度、峭度、方差、最大值、最小值、峰峰值；无量纲指标5个，分别为波形指标、峰值指标、脉冲指标、裕度指标、峭度指标。

11、所述步骤2中，通过一维离散小波包变换对轴承振动信号进行三层小波包分解得到8个小波包，以各小波包对应的归一化能量作为频域特征；

12、小波包的归一化能量定义如下：

13、

14、式中：为进行j层小波包分解后的第i个小波包重构后的能量；为第j层小波分解得到的第i个小波包。

15、采取小波包对信号进行分解时，随着小波包分解层数的增加，信号的完整性也会受到破坏，出于对信号完整性的考虑，本发明在提取小波包归一化能量时采取三层小波包分解，最大程度上保持信号的完整性，同时选取db4作为小波基，它的正交性有利于轴承振动信号频域的局部化分析。

16、所述步骤3中，对提取的时域特征和频域特征进行类别可分性比较，筛选出时域优势特征和频域优势特征。

17、类别可分性需要从两个角度进行判定，一个是同类别内的样本特征彼此之间的差异性，另一个是不同类别彼此之间的差异性，判断类别可分性需要构建类内离差矩阵与类间离差矩阵。

18、类内离差矩阵：

19、

20、其中：n为类别内样本特征的数目，xi为类别中的第i个样本特征，为类别内样本特征的平均矢量。

21、类间离差矩阵：

22、

23、其中：ni为各类别内样本特征的数目，nz为各类别样本特征总的数目，c为类别数，k为类别序号，mk为第k类别内样本特征的平均矢量，mz为各类别总的平均矢量。

24、类别可分性好意味着同类别样本特征间的差异性小，而不同类样本特征的差异性大，这样能够有效提高分类效果。具体地，当sn越小或sj越大时，表示该特征数据的类别可分性越好，因此可将类别可分性定义为：

25、

26、通过类别可分性比较，筛选出正常轴承信号和各类故障轴承信号彼此之间差异更加明显，而同类信号之间差异更小的特征作为优势特征。

27、所述步骤4中，局部线性嵌入lle算法包括以下步骤：

28、步骤4.1：寻找各样本点对应的近邻点：

29、具体来说，计算高维数据空间中每个样本点xi(i＝1,2,…n)与其n-1个样本点之间的距离，根据样本点之间的相互距离大小，选取前k个和xi距离最近的点作为近邻点，样本点之间的距离公式为：

30、dij＝||xi-xj||

31、其中：dij是两点之间的几何距离，xi和xj是高维数据空间里的第i和第j个样本。

32、步骤4.2：由各样本点的近邻点，计算出该样本点的局部重建权值矩阵，计算公式为：

33、

34、式中：表示局部重建权值矩阵，k表示近邻点个数，m表示第m个近邻点，j表示第j个样本点，qi＝(xi-xij)t(xi-xim)，xi表示高维空间第i个样本点，t表示矩阵转置。

35、步骤4.3：通过样本点的局部重建权值矩阵和其近邻点，计算出该样本点的降维输出，也就是将所有的样本点映射到低维空间中，映射条件为：

36、

37、其中：yi是xi的输出向量，yij为yi的第j个近邻点；j＝1,2,…k，k表示近邻点个数；是yi与yij之间的权值，并且需要满足i是单位矩阵。

38、所述步骤4中，通过lle算法进行降维融合，在尽可能地保留原始数据的局部结构的前提下，分别将时域优势特征与频域优势特征降维为一维时域融合特征与一维频域融合特征。

39、所述步骤5中，由步骤4中求得的一维时域融合特征f1与一维频域融合特征f2组成二维联合特征(f1，f2)。

40、所述步骤6中，fcm算法是一种柔性的模糊划分，其目的就是使得被划分到同一类的对象之间相似度最大，而不同类的对象之间相似度最小。

41、具体来说，假定联合特征样本数据集为d＝{d1,d2,…dn}，d1,d2,…dn是样本数据集d中第1个到第n个样本，把这些数据划分为c类，则对应c个标准聚类中心为{s1,s2,…sc}，由此可定义目标函数为：

42、

43、式中：m为隶属度因子，为任意大于1的实数，j＝1,2,…n，n是样本数；dj是第j个样本，si是第i个聚类中心；并且需要满足由此可以推导出隶属度uij的迭代公式为：

44、

45、进一步地，样本聚类中心ci的迭代公式为：

46、

47、所述步骤6中，利用fcm算法，可以将来自不同状态轴承的振动信号对应的二维联合特征划分为不同的类别。聚合分类后能够得到各类别的聚类中心，实际应用时可以根据诊断信号与聚类中心的几何距离来判断故障程度的大小。

48、本发明一种基于特征融合与fcm算法的轴承故障诊断方法，技术效果如下：

49、1)本发明充分利用信号时域特征与频域特征之间的联系，有效提高轴承故障诊断的准确性和可靠性。

50、2)本发明类别可分性比较能够动态筛选优势特征，不再是单一固定的选取特征，使其对于不同的数据也可以表现出较好的适应性和兼容性，以至于能够适用于不同的旋转机械系统。

51、3)本发明降维融合能够将多个特征进行融合，在降低特征维度的同时，综合多个优势特征所具有的特点，进一步增强轴承故障诊断的实用效果。