一种多微观相材料的动态参数反演与动态演变表征方法

本发明涉及一种多微观相材料的动态参数反演与动态演变表征方法，具体地涉及一种基于同步辐射x射线的通过多微观相材料的多参数反演去获取材料内部动态三维演变表征方法，属于动态力学领域。

背景技术：

1、对于实际工程应用，例如高速撞击的实际动态工况中，为了研究复杂组分材料的动态力学性能，需要得到相应的材料参数。

2、实际工况中材料多是复杂的多微观相的各向异性材料，当这种复杂材料受到例如高速撞击的动态加载时，其各微观相的动态参数通常无法单独通过应力应变曲线测得，并且复杂微观相材料在动态工况中的高应变率内部动态三维演变表征一直是研究难点。然而通常的参数反演方法涉及到的材料简单并且加载环境是静态，不适用实际动态工况中的复杂成分材料的参数反演。申请公布号为cn113340732 a虽然提出了基于图像处理，按应变梯度分区，反演了静态拉伸下搅拌摩擦焊铝合金的弹塑性参数。但该方法需要对图像进行预处理，排除图像的转动与平动的影响，根据第三方软件(ncorr)分别计算出图像的平动和转动的位移场以用于后续图像的构造，需要计算应变梯度划分区域，预处理步骤增加了计算量，使整个反演过程复杂化。该方法适用于静态加载工况并且待测参数较少，所以只反演了弹塑性本构参数中最基本的模量、强度、应变硬化系数。该方法虽然考虑了不同区域，但在各区域内材料仍属于各向同性，所以在图像构造时可以直接利用简单的本构关系公式求得位移场，这种简单的公式求解位移场不适用于动态工况复杂各向异性的多微观相材料。并且该方法因为简单静态加载工况，只止步于参数求解，对于不同参数的材料演变并无分析。因此，怎样一体化地反演复杂多微观相材料在动态加载中的多参数同时表征材料内部动态实时三维演变是亟待解决的问题。

技术实现思路

1、为了解决复杂材料的各微观相的多个动态参数难以直接测量或者求解的问题，本发明的目的是提供一种多微观相材料的动态参数反演与动态演变表征方法，能够实现复杂材料在不同应变率下的高速动态实验中多参数的同步求解，通过多组动态实验的图像共同参与动态反演，提高动态参数反演与动态演变表征的精度。

2、本发明的目的是通过下述技术方案实现的：

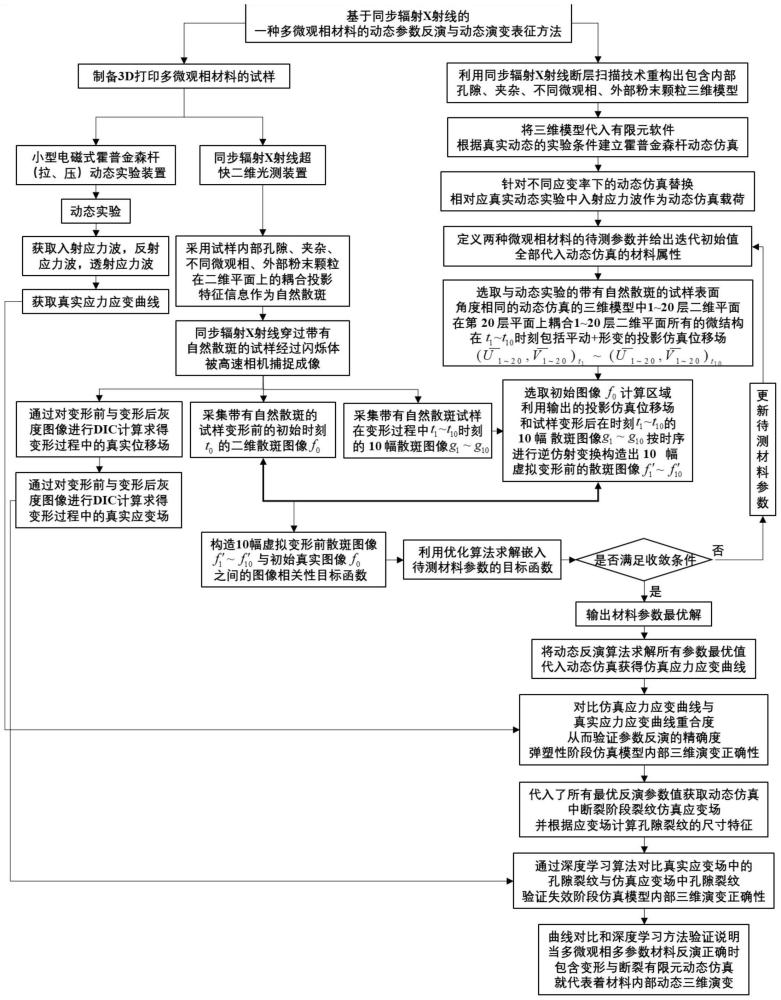
3、本发明公开的一种多微观相材料的动态参数反演与动态演变表征方法，由于试样内部的孔隙、夹杂、不同微观相以及外部的粉末颗粒对同步辐射x射线的吸收程度不同，这些微结构会被耦合投影出自然散斑图像。试样受到小型霍普金森杆(拉、压)的动态加载后发生弹塑性变形后失效破坏，同时经过超快同步辐射x射线照射，试样的变形前自然散斑图像和变形后的n幅随时间变化的自然散斑图像被高速相机采集。利用同步辐射三维ct断层扫描并重构多微观相的试样的三维模型，将多微观相的待测弹塑性和失效参数初值代入关于三维模型的动态霍普金森杆(拉、压)仿真后，输出三维模型的投影仿真位移场，结合位移场和n幅变形后的真实自然散斑图像，逆仿射变换出n幅虚拟变形前图像，从而构建出嵌入了多微观相待测参数的虚拟变形前图像与真实变形前图像之间的图像相关目标函数。通过更新迭代最优弹塑性、失效参数值，优化目标函数，从而求得多微观相的参数最优解。将多微观相参数的反演最优解代入动态仿真模型，求得仿真应力应变曲线和仿真应变场。通过对比仿真应力应变曲线与真实应力应变曲线的重合度，利用对比仿真应变场的裂纹特征和真实应变场的裂纹特征，验证多微观相材料的动态多参数反演结果的正确性，利用验证正确的动态反演结果表征材料内部动态三维演变的实际过程。本发明通用于动态实验中复杂多微观相材料在不同应变率下的多参数的同步求解，并且通过利用参数反演解决材料内部难以实时表征的难点。

4、本发明公开的一种多微观相材料的动态参数反演与动态演变表征方法，包括如下步骤：

5、步骤一、制备带有自然散斑的试样；试样材料包含1～i种微观相，试样具有多种微结构，包括试样内部的孔隙、夹杂、不同微观相，和外部的未烧结粉末颗粒；所述试样在同步辐射x射线照射后，其内部的孔隙、夹杂、不同微观相和外部的粉末颗粒对x射线的吸收程度不同，在垂直于x射线穿透方向的二维平面上耦合投影出因灰度不同而自然形成的散斑信息，称为自然散斑，所有自然散斑构成的图像称为自然散斑图像；

6、步骤二、利用同步辐射x射线断层扫描技术，扫描步骤一中制备的试样，重构出包含内部孔隙、夹杂、不同微观相、外部粉末颗粒三维模型；

7、步骤三、对步骤一中带有自然散斑的试样，同时进行霍普金森杆动态实验和同步辐射x射线的超快二维光测；通过霍普金森杆动态实验，获得入射应力波，反射应力波和透射应力波，三个应力波方向都与杆的轴向一致，试样受到入射应力波加载经历待表征的弹塑性阶段和失效阶段的三维演变，并且进一步求得真实应力应变曲线。通过同步辐射x射线垂直透射试样表面，并且耦合投影出步骤一中的多幅时序下的自然散斑图像，包括初始时刻t0试样变形前的真实自然散斑图像f0和n幅t1～tn时刻试样变形后的真实自然散斑图像的g1～gn；

8、步骤四、将步骤二中获得的试样的三维模型代入有限元软件，按照步骤三中真实的霍普金森杆动态实验，构建关于三维模型的霍普金森杆动态仿真，并且输入与动态仿真相同应变率下的步骤三的中的入射应力波作为动态仿真载荷；

9、步骤五、根据步骤一中的试样材料包含1～i种微观相，定义1～i种微观相的待测材料参数，并给出其迭代初始值；并根据迭代初始值设置材料属性并代入到步骤四的动态仿真中。

10、所述待测材料参数包括弹塑性阶段的弹性参数与johnson-cook本构参数，失效阶段的johnson-cook失效模型的无量纲参数；弹性参数包括弹性模量e和泊松比υ；johnson-cook本构参数包括准静态下的屈服强度a、应变硬化系数b、应变硬化指数n、应变率敏感系数c和温度软化系m；johnson-cook失效模型的无量纲参数包括d1、d2、d3、d4、d5；

11、待测材料参数为待优化量，定义1～i种微观相的所有材料待测参数的迭代初始值p(i)0为其中e(1～i)0是1～i种微观相的弹性模量的迭代初始值，υ(1～i)0是1～i种微观相的泊松比的迭代初始值，a(1～i)0是1～i种微观相的屈服强度的迭代初始值，b(1～i)0是1～i种微观相的应变硬化系数的迭代初始值，n(1～i)0是1～i种微观相的应变硬化指数的迭代初始值，c(1～i)0是1～i种微观相的应变率敏感系数的迭代初始值，m(1～i)0是1～i种微观相的温度软化系数的迭代初始值，d1(1～i)0、d2(1～i)0、d3(1～i)0、d4(1～i)0、d5(1～i)0都是1～i种微观相的johnson-cook失效模型的无量纲参数的迭代初始值；

12、并且将1～i种微观相的待测材料参数的迭代初始值p(1～i)0全部代入步骤四的动态仿真中的材料属性。

13、步骤六、在步骤四的动态仿真中三维模型的第k层平面上，耦合得到1～k层的投影仿真位移场，该投影仿真位移场包括平动与形变，由于步骤五的材料属性中代入了1～i种微观相的待测材料参数，获取t1～tn时刻的n个嵌入了待测材料参数的投影仿真位移场；

14、获取标定的投影仿真位移场的方法具体为：代入步骤五的1～i种微观相的所有材料待测参数的迭代初始值p(i)0到步骤四的动态仿真后，可获得t1～tn时刻动态仿真中三维模型在第k层平面的坐标场上对应的仿真位移场其中u为包括横向平动和横向形变的横向仿真位移场，v为包括纵向平动和纵向的形变的纵向仿真位移场；由于步骤三的同步辐射x射线穿透试样并耦合投影出自然散斑图像，动态仿真要和动态实验设定一致，因此将动态仿真中的三维模型在t1～tn时刻从第1层到第k层平面的仿真位移场全部耦合投影到第k层平面上，从而获取t1～tn时刻的投影仿真位移场

15、步骤七、选取步骤三得到的f0的计算区域，根据步骤六的嵌入了1～i种微观相的待测材料参数的投影仿真位移场和步骤三的t1～tn时刻的g1～gn按时序进行逆仿射变换，构造出嵌入了1～i种微观相的待测材料参数的n幅对应t1～tn时刻的虚拟变形前散斑图像f1′～fn′；

16、具体实现方法为：结合步骤五的待测材料参数的迭代初始值与步骤六中的投影仿真位移场按时序依次对步骤三的n幅t1～tn时刻的真实变形后自然散斑图像g1～gn按以下方法进行逆仿射变换，从而构造出与之相对应的n幅t1～tn时刻虚拟变形前的图像f1′～fn′；

17、

18、其中，x(t)为时刻t0≤t≤tn自然散斑在步骤三的真实变形后图像中的横坐标，y(t)为自然散斑在步骤三的真实变形后图像中的纵坐标；x′(t)为时刻t0≤t≤tn的步骤七的虚拟变形前图像中的横坐标，y′(t)为时刻t0≤t≤tn的步骤七的虚拟变形前图像中的纵坐标；是步骤六的投影仿真横向位移，是步骤六的投影仿真纵向位移；e(1～i)是1～i种微观相的弹性模量，υ(1～i)是1～i种微观相的泊松比，a(1～i)是1～i种微观相的屈服强度，b(1～i)是1～i种微观相的应变硬化系数，n(1～i)是1～i种微观相的应变硬化指数，c(1～i)是1～i种微观相的应变率敏感系数，m(1～i)是1～i种微观相的温度软化系数，d1(1～i)～d5(1～i)是1～i种微观相的johnson-cook失效模型的无量纲参数；x(t)为动态仿真中三维模型的第k层平面中的横坐标，y(t)为动态仿真中三维模型的第k层平面的纵坐标；fs(t)为t1～tn时刻动态仿真的动态仿真载荷，即动态实验中的入射应力波；

19、步骤八、根据图像相关算法的原理，构造步骤七的f1′～fn′与步骤三的f0之间的嵌入了1～i种微观相待测参数的图像相关性目标函数；

20、步骤九、根据优化算法，迭代更新1～i种微观相的待测材料参数，重复五到步骤八的操作，优化步骤八中的目标函数，直到满足收敛条件，此时1～i种微观相的待测材料参数的更新停止，并且此时待测材料参数的更新值即为1～i种微观相的待测材料参数的反演最优结果值；

21、步骤九的具体实现方法为：经过j次迭代，1～i种微观相的待测材料参数更新为将p(1～i)j代入步骤四的动态仿真中，重复步骤五到步骤八，此时嵌入了p(1～i)j的n幅t1～tn时刻的虚拟变形前的图像与步骤三的真实变形前图像f0之间的目标函数值为：

22、

23、其中，ωj为迭代到j次时1～i种微观相的待测材料参数的真实变形前图像f0的计算区域；(x′(p(1～i)j),y′(p(1～i)j))∈ωj，并且表示代入了p(1～i)j而构造出的虚拟变形前图像中的坐标场；(x0,y0)∈ωj，并且表示真实变形前图像中点的坐标场；在时刻t0≤t≤tn，f′((x′(p(1～i)j),y′(p(1～i)j)),t)表示在时刻t构造出的虚拟变形前图像的灰度分布与坐标的函数关系，f((x0,y0),t0)表示在初始时刻t0动态实验中的f0的灰度分布与坐标的函数关系。

24、当c(p(1～i)j)的修正量或者p(1～i)j的修正量满足迭代收敛条件，此时1～i种微观相的待测材料参数的更新值为1～i种微观相的待测材料参数的反演最优结果值；

25、迭代收敛条件为：

26、||c(p(1～i)j)-c(p(1～i)j-1)||≤10-5或||δp(1～i)j-1||≤10-5

27、其中，p(1～i)j＝p(1～i)j-1+δp(1～i)j-1，δp(1～i)j-1＝-he(p(1～i)j-1)-1ja(p(1～i)j-1)；p(1～i)j-1是第j-1次迭代更新时，所述1～i种微观相的待测材料参数值；δp(1～i)j-1是第j-1次所述的1～i种微观相的待测材料参数的修正量；ja(p(1～i)j-1)是c(p(1～i)j-1)的一阶雅可比矩阵；he(p(1～i)j-1)是c(p(1～i)j-1)的二阶黑森矩阵；

28、步骤十、将步骤九的1～i种待测材料参数的反演最优结果值代入步骤四的动态仿真中，动态仿真包括弹塑性阶段的与失效阶段的三维模型中1～i种微观相的整个动态过程的三维演变；通过验证1～i种待测材料参数的反演最优结果值的正确性，从而获取对应的动态仿真中塑性阶段与失效阶段的三维演变。具体方法包括：

29、1)、将步骤九的结果值代入步骤四的动态仿真中，得到仿真应力应变曲线，并且将仿真应力应变曲线与步骤三的真实应力应变曲线进行对比，通过两条曲线的重合度验证步骤九的参数反演结果的精确度，从而获取步骤四中动态仿真中三维模型在弹塑性阶段内部三维演变的正确性；

30、2)、根据图像相关算法，通过步骤三的f0和g1～gn求得真实应变场；同时代入步骤九求得的待测参数到步骤四的动态仿真，输出仿真应变场；通过深度学习算法对比识别真实应变场中的孔隙裂纹特征与仿真应变场中孔隙裂纹特征，从而获取步骤四中动态仿真中三维模型在失效阶段内部三维演变的正确性。

31、有益效果：

32、1、现有的材料参数反演方法涉及到的材料组分简单并且加载环境是静态加载，不适用实际动态工况中的复杂成分材料的多参数的同时求解。并且在动态加载中，目前只有宏观总体材料参数的获取方式，对于材料当中的各微观相的材料参数，难以分别直接测量或者计算求得。本发明公开的一种多微观相材料的动态参数反演与动态演变表征方法，针对实际工程应用中的复杂材料含有多种微观相，考虑了动态加载的时间与应变率因素，结合同步辐射x射线光测技术、动态实验、动态仿真，集成了数字图形相关算法，构建了嵌入多微观相的待测弹塑性和失效参数初值的虚拟图像与真实图像之间的图像相关目标函数，从而通过优化算法同时反演求解出各微观相的多个参数。实现了复杂材料在不同应变率下的高速动态实验中多参数的同步求解。

33、2、现有的反演结果的验证方式往往采用实验测得的应力应变信息进行本构拟合，通过拟合出的本构模型求解参数。但这种传统方法却不适用于实际工况中动态加载下的多微观相复杂材料，因为对于一个整体的复杂材料，通常测得的都是宏观复杂材料的应力应变信号，然而其内部的各微观相参数是无法分别直接测得的，各微观相各自的应力应变信号也无法分别获取，因此也就无法通过传统的本构拟合直接计求得，也就无法验证通过反演方法获取的多微观相的材料参数值。但是又需要对复杂材料内部各个微观相的动态参数反演结果的正确性进行验证，因此本发明公开的一种多微观相材料的动态参数反演与动态演变表征方法，通过将动态反演参数的结果值回代到动态仿真中，对比仿真与实验的结果，利用宏观双曲线的重合度和深度学习模拟裂纹与真实裂纹的特征，巧妙地验证了多微观相的所有待测材料参数的动态反演结果的正确性。而且相比较传统的本构拟合求解计算参数，本方法操作简便，避免了传统本构拟合的误差。最后将验证过的参数反演结果代入动态仿真，利用动态仿真代替材料内动态演变的实际过程，同时也表征了材料内部的动态三维演变。

34、3、本发明公开的一种多微观相材料的动态参数反演与动态演变表征方法，具有通用性，适用于多组应变率的各类型动态实验中的多参数同时反演，在反演过程中，只需要替换初始动态仿真的输入载荷和参与逆仿射变换的真实图像，提高了反演求解的效率，提高了动态参数反演的精度。并且构造虚拟图像与真实图像相关运算的反演过程非常便捷。通过直接对图像的处理省去了传统方法中对图像预处理的过程。