一种基于电流环扰动的并网变流器频率耦合导纳测量方法

本发明涉及一种基于电流环扰动的并网变流器频率耦合导纳测量方法，属于新能源并网变换器分析与控制。

背景技术：

1、可再生能源的装机容量持续增长，已经引起了电网中一系列的宽带振荡问题。基于并网变流器阻抗的分析方法是一种有效的方法，近年来被大量学者进行广泛研究。阻抗分析法是利用并网变流器的等效阻抗和电网阻抗来分析系统的稳定性。因此，需要准确的获取并网变流器的阻抗或导纳。

2、频率耦合导纳能够反映并网变流器的频率耦合特性，近年来一直被持续研究。现有的频率耦合导纳测量方法需要研制相应电压等级和容量的测量装备，将其串联到线路上，通过向并网变流器注入谐波来测量各个频率点的等效频率耦合导纳。然而，此方法的硬件成本较高，便捷性较差。

技术实现思路

1、针对上述问题，本发明提供了一种基于电流环扰动的并网变流器频率耦合导纳测量方法，无需研制导纳测量装备，能够大幅度降低测量成本并提高测量的便捷性。

2、术语解释：

3、1、伯德图：伯德图是所有控制系统在频域中进行分析的工具。它包括两个图，一个是幅频特性图，一个是相频特性图。幅频特性图表示了一个控制系统的输入和输出之间的幅值衰减程度；相频特性图表示此控制系统的输入和输出之间的相位差异。幅值和相位的变化都能通过伯德图观察出，所以控制系统在频率域上的特性可以进行数学分析。

4、2、零极点对消方法：控制系统在频域中可以等效为一个传递函数，这个传递函数是一个关于s的方程。传递函数的分母等于0的点，为传递函数的极点；传递函数分子等于0的点，为传递函数的零点。当通过调整传递函数的分子和分母的系数时，如果能使得分子和分母的某个式子相互抵消，那么相当于消除了一个零点和一个极点，简化了传递函数，使得控制系统分析起来更方便。

5、3、正序电压：正序电压为a、b、c三相电压的初始相位依次滞后120度，这也是正常状态下电力系统的相序，即b相的初始相位=a相的初始相位-120度；c相的初始相位=b相的初始相位-120度。

6、4、负序电压：负序电压为a、b、c三相电压的初始相位依次超前120度，即b相的初始相位=a相的初始相位+120度；c相的初始相位=b相的初始相位+120度。

7、本发明的技术方案如下：

8、一种基于电流环扰动的并网变流器频率耦合导纳测量方法，包括如下步骤：

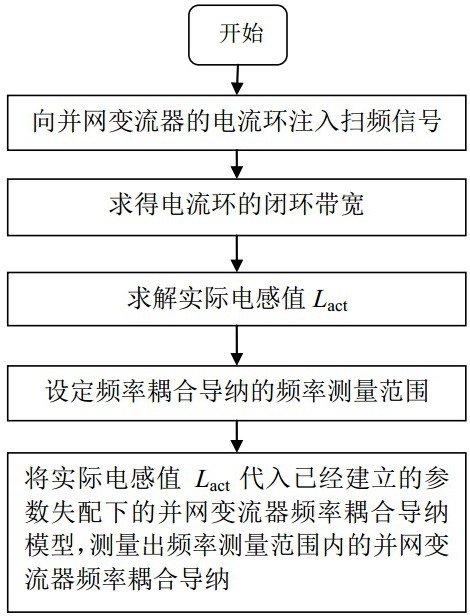
9、s1：向并网变流器的电流环注入扫频信号；

10、s2：根据电流环的扫频信号注入得到的电流环的d轴参考值 idref和电流反馈值 id的实测数据，求得电流环的闭环带宽；

11、s3：根据电流环实际带宽求解实际电感值 lact；

12、s4：设定频率耦合导纳的频率测量范围；

13、s5：将实际电感值 lact代入已经建立的参数失配下的并网变流器频率耦合导纳模型，测量出频率测量范围内的并网变流器频率耦合导纳。

14、优选的，步骤s2中，对电流环的d轴参考值 idref和电流反馈值 id进行快速傅里叶变换，得到各个频率下电流环的d轴参考值 idref和电流反馈值 id两个变量的幅值和相位，以频率为横坐标，将各个频率下的幅值依次相连形成伯德图中的幅频特性图，将各个频率下的相位依次相连形成伯德图中的相频特性图，最终绘制出完电流环完整的伯德图；伯德图的幅频特性图中，当幅值下降-3db时所对应的频率称为电流环的闭环带宽；当伯德图绘制好后，可直接从幅频特性图中寻找纵坐标为-3db时所对应的频率，从而求出电流环的闭环带宽。

15、优选的，步骤s3中，当电流环按照零极点对消的方法进行pi控制器参数整定时，电流环比例系数 kip和积分系数 kii的计算方法如下：

16、（1）

17、其中， ωid为电流环的期望带宽， rs为理论电阻值， ls为理论电感值；

18、电流环的频域传递过程如图3所示，因此，电流环的闭环传递函数 gic(j ω)如下：

19、（2）

20、其中， ts为控制周期； ω为角频率；j为复数，即虚数；

21、 f和 h的表达式如下：

22、（3）

23、其中， kr为实际电阻值和理论电阻值的比值， kl为实际电感值 lact和理论电感值 ls的比值；

24、当 h在较低带宽下近似等于0。此外， f的值远大于 h。因此，在闭环传递函数建模中可以忽略 h的影响，因此，式（2）可以被重写如下：

25、 （4）

26、当电感和电阻的实际参数失配时，电流环实际带宽的表达式如下：

27、（5）

28、其中，是参数失配下的电流环实际带宽；

29、由于实际中远小于，由式（3）知， f约等于 ls和 lact的比值，带入式（5），可得到简化后的式（5）如下：

30、（6）

31、式（6）描述了实际电感值 lact发生变化时，电流环实际带宽与电流环的期望带宽 ωid的定量变化；采用欧拉法对式（6）进行离散求解，即在很小步长下求取近似解，并将近似解连成一条曲线；以式（6）中的 ωid为横坐标，为纵坐标，两者之间无法直接求解出固定的表达式，当 ls等于 lact时，离散求解的曲线为图4中电感参数准确的曲线，当 ls小于 lact时，离散求解的曲线为图4中电感参数失配的曲线；

32、根据电感参数准确的曲线、电感参数失配的曲线和式（6），可以得到 ls和 lact的关系如下式：

33、（7）

34、其中， ωid1为固定的电流环期望带宽， ωid2为电感参数失配后对应的等效期望带宽；当pi控制器的参数确定后， ωid1是一个不变的已知量；如果电感参数准确，电流环的闭环带宽 ωb的角频率对应的频率 fb1，如图4；当电感参数失配时，向电流环注入扫频信号后可以求得实际的电流环带宽 fb2，即的角频率对应的频率，如图4，在电感参数失配时，通过向电流环注入扫频信号得到电流环的实际带宽，将其带入式（5）中，求得的 ωid即为求得 ωid2；

35、将 ωid1、 ωid2、 ls代入式（7），即可求出准确的实际电感值 lact。

36、优选的，步骤s5中，频率耦合特性如下：

37、（8）

38、其中， ip是并网变流器的电流在任一正序电压扰动频率 fp处的频域响应分量， ip2是并网变流器的电流在频率为 fp2处的频域响应分量，其中 fp2= fp-2 f1， f1为基波频率，其值为50hz； vp是并网变流器的电压在频率为任一正序电压扰动频率 fp处的频域响应分量， vp2是并网点电压在频率为 fp2处的频域响应分量； y11是正序自导纳， y12是负序耦合导纳， y21是正序耦合导纳， y22是负序自导纳；

39、 y11、 y12、 y21和 y22的表达式如下：

40、（9）

41、其中， km是脉宽调制增益， b1是直流电压频域小信号模型中电压频率为 fp2的系数， b2是直流电压频域小信号模型中电压频率为 fp的系数， b3是直流电压频域小信号模型中电流频率为 fp2的系数， b4是直流电压频域小信号模型中电流频率为 fp的系数； d2是a相调制电压小信号在频率 fp1处的电压频率为 fp2的系数， d4是a相调制电压小信号在频率 fp1处的电流频率为 fp2的系数； d6是a相调制电压小信号在频率 fp处的电压频率为 fp2的系数， d8是a相调制电压小信号在频率 fp处的电流频率为 fp的系数； sp是在 fp处将 s域转换成频率域后的值， sp2是在频率 fp2处将 s域转换成频率域后的值； e1和 e2的表达式如下：

42、（10）

43、其中， d1是a相调制电压小信号在频率 fp1处的直流电压系数， fp1= fp- f1； d5是a相调制电压小信号在频率 fp处的直流电压系数， m1是a相调制信号在基频下的频域稳态分量，是 m1的共轭。

44、优选的， b1~ b4是通过交直流功率平衡方程在频域下的传递过程得到的，并网变流器的交直流功率平衡方程如下：

45、（11）

46、其中， vdc是直流母线电压， idc是直流侧总电流 idc的直流分量， cdc是直流母线电容， via是并网变流器a相交流调制电压， vib是并网变流器b相交流调制电压， vic是并网变流器c相交流调制电压， ia是并网变流器a相交流调制电流， ib是并网变流器b相交流调制电流， ic是并网变流器c相交流调制电流；

47、并网变流器与电网之间的基尔霍夫定律表达式如下：

48、（12）

49、将式（11）和式（12）进行频域线性化，即可得到直流母线电压的频域小信号的表达式如下：

50、（13）

51、通过公式（13）即可得到 b1~ b4的值；

52、式（11）~式（13）表明， b1~ b4可以通过交直流功率平衡方程在频域下的传递过程得到。

53、优选的， d1~ d8是通过锁相环的频域传递过程、电压环和电流环的频域传递过程得到的，锁相环的传递过程如下：

54、（14）

55、其中， θpll是锁相环输出的角度， vq是三相电压经过派克变换后的q轴电压分量， gpll( s)是锁相环的传递函数，其表达式如下：

56、（15）

57、其中， kpp为锁相环的比例系数， kpi为锁相环的积分系数，s表示s域，与时域t类似，s的取值范围是负无穷到正无穷；

58、电压环的传递过程如下：

59、（16）

60、其中， vdcref为电压环给定直流母线的电压参考值， gv( s)为电压环传递函数，其表达式如下：

61、（17）

62、其中， kvdcp为电压环比例系数， kvdci为电压环积分系数；

63、电流环的传递过程如下：

64、（18）

65、其中， ucd是电流环输出的d轴调制电压 ucd， ucq是电流环输出的q轴调制电压， iq是电流环的q轴实际电流值， kd为解耦系数， gi( s)是电流环传递函数，其表达式如下：

66、（19）

67、其中， ts是控制器的控制周期；

68、对式（14）~式（20）进行频域线性化，再通过反派克变换即可得到并网变流器a相等效电压的频域小信号模型，其表达式如下：

69、（20）

70、其中， vdcp1是直流母线电压的基频分量； d3是a相调制电压小信号在频率 fp1处的电压频率为 fp的系数， d3与 d2为相反数， d7是a相调制电压小信号在频率 fp处的电压频率为 fp的系数， d7与 d6为相反数。值得注意的是， d1~ d8的值可同时计算得到，但 d3、 d7并未参与导纳的计算。

71、本发明未详尽之处，均可参见现有技术。

72、本发明的有益效果为：

73、本发明通过对电流环路注入扫频信号来实现。对电流环的闭环带宽与控制器参数之间的关系进行详细分析，可以用来求解实际电感值。因此，当设置频率范围时，带入已建立的频率耦合导纳模型，可以精确地测量并网变流器频率耦合导纳。此方法在电感参数失配的情况下仍能准确测量频率耦合导纳，且不需要在主电路侧研制导纳测量装备，大大降低频率耦合导纳的测量成本，提高测量的便捷性。