激光跟踪仪多边测量场的优化空间坐标解算方法及系统

本发明涉及三维坐标测量的，具体地，涉及激光跟踪仪多边测量场的优化空间坐标解算方法及系统，更为具体地，涉及激光跟踪仪多边测量场对特定待测空间的优化空间坐标解算方法及系统。

背景技术：

1、在大尺度高柔性加工制造领域，大尺寸多轴机床及工业机器人应用十分广泛，其空间误差综合反映了设备的加工能力，限制了其工业应用场景。基于激光跟踪仪的空间误差标定是常用的机床及机器人空间误差校准方法，本质归属工业三维坐标测量问题。单台激光跟踪仪能在自身固有的测量坐标系中标定靶标的球坐标方位。在单台激光跟踪仪直接输出靶标的球坐标标定结果中，其距离值通过高精度激光干涉测距得到，精度高，不确定度较小，但两个角度值精度相对较低，也使得单台激光跟踪仪不能直接用于高精度的机床及工业机器人标定。

2、基于多台激光跟踪仪组建多边测量场的空间误差标定是常用的机床及机器人空间误差校准方法。该方法的基本思路是在空间内四个及以上的非共线非共面位置设置激光跟踪仪基站，同时观测一个靶标位置。针对四台干涉测距模式的激光跟踪仪组网模式，传统的三维坐标解算模型分为两个步骤。第一步是测量场基站位置及死径标定，需要至少16个校准点参与非线性最小二乘优化问题的迭代计算。第二步是基于第一步的标定结果进行待测点坐标计算，四个激光跟踪仪为测量场内任意空间点的三维位置解算提供了计算冗余度。值得注意的是，传统坐标解算模型在前期测量场标定过程中，无论多少校准点参与基站位置迭代，测量场位置及死径标定始终与实际空间位置存在偏差，而这一标定的误差会成为第二步空间点坐标解算的系统性偏差。

3、专利文献cn111811396a(申请号：202010530001.2)公开了一种基于平面约束的多边法激光跟踪三维坐标测量方法。通过在传统多边测量场中引入平面约束，为模型提供冗余的优化方程，提高多边系统的标定精度，进而提高多边系统对空间点三维坐标测量的精度。该方法需要增加多个光学面包板作为额外的校准设备，能够对测量场参数标定起到一定的精度提升作用，但其算法后续的平面拟合也引入了新的误差因素，且无法避免测量场参数标定对于后续点坐标解算的系统性影响。

技术实现思路

1、针对现有技术中的缺陷，本发明的目的是提供一种激光跟踪仪多边测量场的优化坐标解算方法及系统。

2、根据本发明提供的一种激光跟踪仪多边测量场的优化坐标解算方法，包括：

3、步骤s1：搭建激光跟踪仪多边测量场；

4、步骤s2：基于hammersley序列[h]m×n生成候选校准点集合，与待测点集合合并为实测测量点集合；

5、步骤s3：利用多台激光跟踪仪实时跟踪靶标的位置，输出各实测测量点处的距离测量值；

6、步骤s4：基于hammersley序列生成参考校准点集合，计算参考校准点集合的点平均距离，以空间均匀度为基本准入原则从候选校准点集合中筛选面向各待测点坐标解算的特定校准点集，使用特定校准点集对应的测距数据集进行各待测点的空间坐标解算。

7、优选地，所述步骤s1采用：

8、将多台激光跟踪仪连接组网，且多台激光跟踪仪固定于预设的基站位置；

9、所述多台激光跟踪仪在待测空间中的摆放位置不能共面；任意三台激光跟踪仪的位置不能共线；同时，校核当前多边测量场的可测空间范围与测量条件。

10、优选地，所述步骤s2采用：

11、步骤s2.1：生成维度为m，长度为n的hammersley序列[h]m×n；

12、步骤s2.2：依据待测空间范围对生成的hammersley序列进行区间放缩，生成候选校准点集合pcc＝{pcc,i},i＝1,2,…,n；

13、步骤s2.3：合并候选校准点集合pcc与待测点集合pm＝{pm,k},k＝1,2,…,k为实测测量点集合。

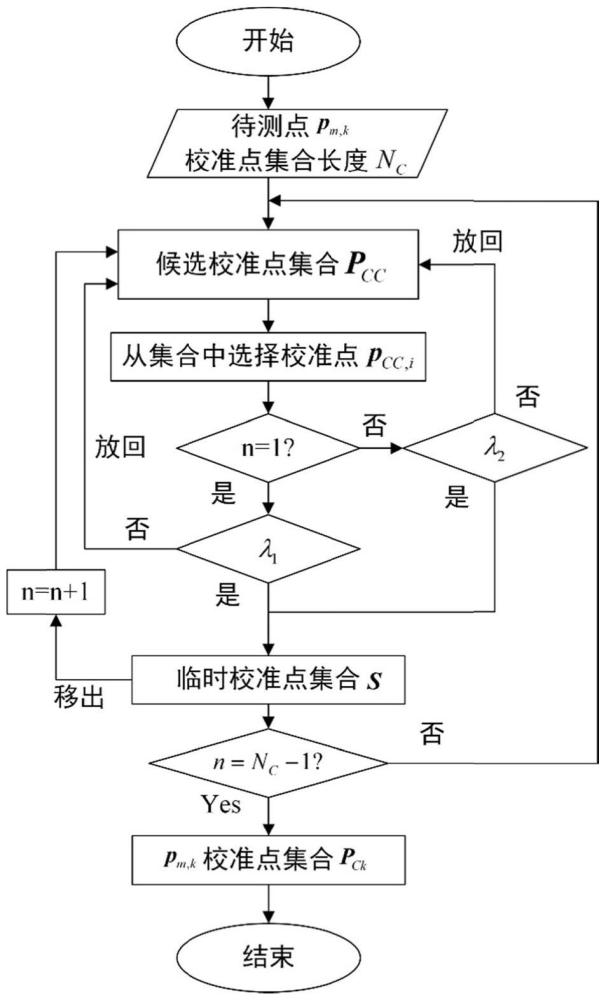
14、优选地，所述步骤s3采用：

15、步骤s3.1：依据测量仪器实际情况设置靶标在各实测测量点处的停止时间，依据实测测量点的标称空间坐标值编写机床数控系统可识别的nc程序；

16、步骤s3.2：调节四台跟踪仪的俯仰角以及方位角使其锁定固定在运动装置末端的靶标；

17、步骤s3.3：控制机床各运动轴运动至极限测量位置，若存在断光现象，则需重新调节摆放的基站位置、各基站位置处跟踪仪的姿态或更正可测量的空间范围，直至各轴运动范围内均不发生断光现象，判定为多边测量场测量条件充分；

18、步骤s3.4：当多边测量场测量条件充分时，则运行nc程序，记录各实测测量点处多台跟踪仪输出的距离测量值，直至nc程序运行完毕。

19、优选地，所述步骤s4采用：

20、步骤s4.1：生成参考校准点集合pcr并计算任意两点之间的平均距离

21、生成维度为m，长度为nc的hammersley序列依据待测空间范围进行放缩，生成包含nc个点的机床坐标系下的参考校准点集合pcr＝{pcr,i},i＝1,2,…,nc，计算校准点集合中任意两点的距离并求平均值：

22、

23、步骤s4.2：为待测点pm,k坐标解算选择第一个特定校准点pck,1；

24、遍历候选校准点池pcc＝{pcc,i},i＝1,2,…,n，以λ1为准入原则选择第一个特定校准点pck,1：

25、

26、其中，ls,i＝||pcc,i-pm,k||2,i＝1,2,…,n；选择完毕后将pck,1移出pcc候选点池；

27、步骤s4.3：为待测点pm,k坐标解算选择其余nc-2个特定校准点；

28、选择第j个校准点pck,j,j＝2,3,…,nc-1，此时前j-1个校准点已通过前置步骤选择完毕，pcc候选点池中包含n-j-1个候选校准点；

29、从当前pcc候选点池中选择pcc,i,i＝1,2,…,n-j-1，与已选择的j-1个校准点以及待测点pm,k构成临时点集合s＝{pm,k；pck,1；pck,2；…；pck,j-1；pcc,i}；

30、记s＝{xtemp,m},m＝1,2,…,j+1，计算此临时校准点集合s中点xtemp,m,m＝1,2,…,j+1对应的独占球直径：

31、

32、以xtemp,m,m＝1,2,…,j+1为圆心，以r(xtemp,m)＝m(xtemp,m)/2为半径的独占球体积可通过下式计算：

33、

34、已知待测空间为a，其包含了所有的待测点及候选校准点{pcc,pm}∈a，容积记为v(a)，则对应于点pcc,i,i＝1,2,…,n-j-1的临时校准点集合s的空间均匀度可通过下式计算：

35、

36、遍历pcc候选点池中的n-j-1个候选校准点，第j个校准点pck,j的准入原则为λ2：

37、λ2＝max(λu)

38、选择完毕后将pck,j移出候选点池pcc，进行第j+1个校准点的选择，直至校准点数量满足预设要求；

39、步骤s4.4：整合针对待测点pm,k的长度为nc-1的特定校准点集合pck＝{pck,i},i＝1,2,...,nc-1。

40、优选地，所述步骤s4采用：

41、设激光跟踪仪的四个基站位置为ti,i＝1,2,3,4，各基站对应的死径为di,i＝1,2,3,4，实测测量点集合为{pcc,pm}，包括候选校准点集合pcc＝{pcc,i},i＝1,2,…,n以及待测点集合pm＝{pm,k},k＝1,2,…,k；

42、待测点pm,k的特定校准点集合为pck＝{pck,j},j＝1,2,…,nc-1，记跟踪仪ti对于pm,k的距离观测数据为lk,i，对于pck中各点pck,j,j＝1,2,…,nc-1观测数据记为lck,ij,i＝1,2,3,4,j＝1,2,…,nc-1；

43、依据两点间距离公式，针对pm,k的坐标解算可以列出包含4×nc个方程的非线性方程组：

44、||[ti]m-[pm,k]m||2＝di+lk,i

45、||[ti]m-[pck,j]m||2＝di+lck,ij

46、其中，i＝1,2,3,4,j＝1,2,…,nc-1，则解算pm,k的过程可以视下述非线性优化问题的求解：

47、

48、上述优化问题所有的未知量可以归于一个目标求解矢量：

49、

50、要使得上述非线性优化问题有解，nc取值需满足下述不等式条件：

51、4*3+4+3*nc<4*nc

52、nc>16，对应候选校准点集合包含的点个数建议n＝10*nc；使用levenberg-marquardt算法求解上述优化问题即可得到pm,k的坐标解算结果。

53、根据本发明提供的一种激光跟踪仪多边测量场的优化坐标解算系统，包括：

54、模块m1：搭建激光跟踪仪多边测量场；

55、模块m2：基于hammersley序列[h]m×n生成候选校准点集合，与待测点集合合并为实测测量点集合；

56、模块m3：利用多台激光跟踪仪实时跟踪靶标的位置，输出各实测测量点处的距离测量值；

57、模块m4：基于hammersley序列生成参考校准点集合，计算参考校准点集合的点平均距离，以空间均匀度为基本准入原则从候选校准点集合中筛选面向各待测点坐标解算的特定校准点集，使用特定校准点集对应的测距数据集进行各待测点的空间坐标解算。

58、优选地，所述模块m1采用：

59、将多台激光跟踪仪连接组网，且多台激光跟踪仪固定于预设的基站位置；

60、所述多台激光跟踪仪在待测空间中的摆放位置不能共面；任意三台激光跟踪仪的位置不能共线；同时，校核当前多边测量场的可测空间范围与测量条件。

61、优选地，所述模块m2采用：

62、模块m2.1：生成维度为m，长度为n的hammersley序列[h]m×n；

63、模块m2.2：依据待测空间范围对生成的hammersley序列进行区间放缩，生成候选校准点集合pcc＝{pcc,i},i＝1,2,…,n；

64、模块m2.3：合并候选校准点集合pcc与待测点集合pm＝{pm,k},k＝1,2,…,k为实测测量点集合；

65、所述模块m3采用：

66、模块m3.1：依据测量仪器实际情况设置靶标在各实测测量点处的停止时间，依据实测测量点的标称空间坐标值编写机床数控系统可识别的nc程序；

67、模块m3.2：调节四台跟踪仪的俯仰角以及方位角使其锁定固定在运动装置末端的靶标；

68、模块m3.3：控制机床各运动轴运动至极限测量位置，若存在断光现象，则需重新调节摆放的基站位置、各基站位置处跟踪仪的姿态或更正可测量的空间范围，直至各轴运动范围内均不发生断光现象，判定为多边测量场测量条件充分；

69、模块m3.4：当多边测量场测量条件充分时，则运行nc程序，记录各实测测量点处多台跟踪仪输出的距离测量值，直至nc程序运行完毕。

70、优选地，所述模块m4采用：

71、模块m4.1：生成参考校准点集合pcr并计算任意两点之间的平均距离

72、生成维度为m，长度为nc的hammersley序列依据待测空间范围进行放缩，生成包含nc个点的机床坐标系下的参考校准点集合pcr＝{pcr,i},i＝1,2,…,nc，计算校准点集合中任意两点的距离并求平均值：

73、

74、模块m4.2：为待测点pm,k坐标解算选择第一个特定校准点pck,1；

75、遍历候选校准点池pcc＝{pcc,i},i＝1,2,…,n，以λ1为准入原则选择第一个特定校准点pck,1：

76、

77、其中，ls,i＝||pcc,i-pm,k||2,i＝1,2,…,n；选择完毕后将pck,1移出pcc候选点池；

78、模块m4.3：为待测点pm,k坐标解算选择其余nc-2个特定校准点；

79、选择第j个校准点pck,j,j＝2,3,…,nc-1，此时前j-1个校准点已通过前置步骤选择完毕，pcc候选点池中包含n-j-1个候选校准点；

80、从当前pcc候选点池中选择pcc,i,i＝1,2,…,n-j-1，与已选择的j-1个校准点以及待测点pm,k构成临时点集合s＝{pm,k；pck,1；pck,2；…；pck,j-1；pcc,i}；

81、记s＝{xtemp,m},m＝1,2,…,j+1，计算此临时校准点集合s中点xtemp,m,m＝1,2,…,j+1对应的独占球直径：

82、

83、以xtemp,m,m＝1,2,…,j+1为圆心，以r(xtemp,m)＝m(xtemp,m)/2为半径的独占球体积可通过下式计算：

84、

85、已知待测空间为a，其包含了所有的待测点及候选校准点{pcc,pm}∈a，容积记为v(a)，则对应于点pcc,i,i＝1,2,…,n-j-1的临时校准点集合s的空间均匀度可通过下式计算：

86、

87、遍历pcc候选点池中的n-j-1个候选校准点，第j个校准点pck,j的准入原则为λ2：

88、λ2＝max(λu)

89、选择完毕后将pck,j移出候选点池pcc，进行第j+1个校准点的选择，直至校准点数量满足预设要求；

90、模块m4.4：整合针对待测点pm,k的长度为nc-1的特定校准点集合pck＝{pck,i},i＝1,2,...,nc-1；

91、所述模块m4采用：

92、设激光跟踪仪的四个基站位置为ti,i＝1,2,3,4，各基站对应的死径为di,i＝1,2,3,4，实测测量点集合为{pcc,pm}，包括候选校准点集合pcc＝{pcc,i},i＝1,2,…,n以及待测点集合pm＝{pm,k},k＝1,2,…,k；

93、待测点pm,k的特定校准点集合为pck＝{pck,j},j＝1,2,…,nc-1，记跟踪仪ti对于pm,k的距离观测数据为lk,i，对于pck中各点pck,j,j＝1,2,…,nc-1观测数据记为lck,ij,i＝1,2,3,4,j＝1,2,…,nc-1；

94、依据两点间距离公式，针对pm,k的坐标解算可以列出包含4×nc个方程的非线性方程组：

95、||[ti]m-[pm,k]m||2＝di+lk,i

96、||[ti]m-[pck,j]m||2＝di+lck,ij

97、其中，i＝1,2,3,4,j＝1,2,…,nc-1，则解算pm,k的过程可以视下述非线性优化问题的求解：

98、

99、上述优化问题所有的未知量可以归于一个目标求解矢量：

100、

101、要使得上述非线性优化问题有解，nc取值需满足下述不等式条件：

102、4*3+4+3*nc<4*nc

103、nc>16，对应候选校准点集合包含的点个数建议n＝10*nc；使用levenberg-marquardt算法求解上述优化问题即可得到pm,k的坐标解算结果。

104、与现有技术相比，本发明具有如下的有益效果：

105、1、本发明提出的坐标解算方法无需预标定多边测量场的参数，避免了测量场参数标定误差对于空间坐标解算精度的系统性影响。

106、2、本发明提出的坐标解算方法能够在较大程度上提升空间坐标各维度的绝对解算精度，并降低解算的不确定度，算法稳定性较强。

107、3、本发明不改变多边测量场的架构过程，无需借助第三方测量设备及标准件，实现效率高，面向相同工业测量基本问题的普适性及拓展性较强。